METODY NUMERYCZNE

Cel przedmiotu - zapoznanie się z podstawami metod:

• rozwiązywania układów równań liniowych;

• oszacowania błędów obliczeń numerycznych;

• rozwiązywania równań nieliniowych;

• różniczkowania i całkowania numerycznych;

• interpolacji i aproksymacji funkcji;

• rozwiązywania równań różniczkowych;

• itp.

Literatura

1. Povstenko J., Wprowadzenie do metod numerycznych. - Warszawa: EXIT, 2002.

2. Fortuna Z., Macukow B., Wąsoski J., Metody numeryczne. - Warszawa: PWN, 2001.

3. Stoer J., Wstęp do metod numerycznych. - Warszawa: PWN, 1979.

4. Stoer J., Bulifsch R., Wstęp do metod numerycznych. - Warszawa: PWN, 1980.

5. Ralson A. Wstęp do analizy numerycznej. - Warszawa: Państwowe Wydawnictwo Naukowe, 1983.

6. Bjorch A., Dahlquist G., Metody numeryczne. - Warszawa: Państwowe Wydawnictwo Naukowe, Warszawa, 1987.

7. Dryja M., Jankowscy J. i M., Przegląd metod i algorytmów numerycznych. - Warszawa: Wydawnictwa Naukowo-Techniczne, 1988.

8. Бахвалов Н. С., Численные методы. - Москва: Наука, 1975.

9. Marciniak A., Gregulec D., Kaczmarek J., Podstawowe procedury numerycz­ne w języku Turbo Pascal. - Poznań: Nakom, 2000.

10. Kiełbasiński A., Schwetlick H., Numeryczna algebra liniowa. - Warszawa: Wydawnictwo Naukowo-Techniczne, 1992.

11. Kincaid D., Cheney W., Analiza numeryczna. - Warszawa: Wydawnictwo Naukowo-Techniczne, Warszawa, 2006.

Rozdział I

Wiadomości wstępne

1.1. Ciągi nieskończone.

Definicja 1.1. Funkcje

,

gdzie
jest dowolnym niepustym zbiorem, nazywamy ciągiem skończonym
wyrazowym, a funkcje

ciągiem liczbowym
wyrazowym.

Definicja 1.2. Ciągiem nieskończonym nazywamy funkcję
, która odwzorowuje zbiór
liczb naturalnych dodatnich w niepusty zbiór

.

Jeżeli mamy odwzorowanie

,

to mówimy o ciągu nieskończonym liczbowym.

Ciągi liczbowe
wyrazowe zapisujemy w postaci

,

zaś ciąg liczbowy nieskończony odnotujemy jak

.

1.2. Przestrzenie liniowe.

Definicja 1.3. Przestrzenią liniową
nad ciałem liczb rzeczywistych
nazywamy zbiór z działaniem wewnętrznym (dodawanie)

i działaniem zewnętrznym (mnożenie przez liczbę rzeczywistą)

.

•  Dodawanie w zbiorze
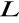
  określa strukturę grupy przemiennej, w której element neutralny oznaczamy przez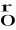
  oraz element przeciwny do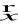
  jako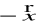
  .

•  Mnożenie wektorów przez liczby rzeczywisty jest łączne

,

oraz element neutralny jest jedynka

.

•  Zakładamy prawa rozdzielności

;

.

Definicja 1.4. Określimy
wymiarową przestrzeń arytmetyczną przez iloczyn kartezjański

,

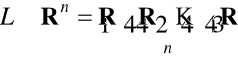
działania na elementach której

,

określimy następująco

,

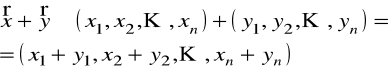
oraz

.

Definicja 1.5. Określimy
wymiarową przestrzeń arytmetyczną przez iloczyn kartezjański

,

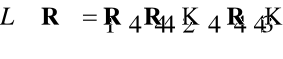
działania na elementach której

,

określimy następująco

,

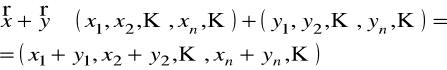
oraz

.

Definicja 1.6. Zbiór funkcji rzeczywistych ciągłych
lub całkowalnych
określonych w przedziale
tworzą przestrzeń liniową jeśli dla elementów zbioru
są określone działania

;

,

albo dla funkcji całkowalnych

;

.

Definicja 1.7. Odwzorowaniem liniowym (homomorfiz­mem) nazywamy funkcję

spełniającą warunki

;

,

gdzie
jest przestrzenią linową.

Definicja 1.8. Odwzorowanie liniowe (homomorfizm) wzajemnie jednoznaczne nazywamy izomorfizmem.

Definicja 1.9. Powłoką liniową rozpiętą na wektorach

nazywamy wyrażenie

.

Definicja 1.10. Wektory
nazywamy liniowo niezależnymi, jeśli tożsamość

spełnia się wtedy i tylko wtedy, gdy wszystkie współczynniki
są równe zero. W przeciwnym razie wektory
nazywamy liniowo zależnymi.

Definicja 1.11. Liniowo niezależny zbiór wektorów
nazywamy bazą przestrzeni liniowej
, jeśli każdy wektor
nie należący do tego zbioru może być zapisany w postaci

,

gdzie współczynniki rozwinięcia
wtedy nazywamy współrzędnymi wektora
.

Odstęp liryczny. Liniowa niezależność funkcji.

Definicja 2.1. Funkcje
,
, które określone w przedziale otwartym
, są liniowo niezależne, jeżeli tożsamość

,
,

zachodzi wtedy i tylko wtedy, kiedy

,

gdzie
— liczby rzeczywiste (
).

Twierdzenie 2.2. Jeśli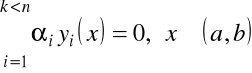
, to funkcje
,
, są liniowo zależne.

Twierdzenie 2.3. Jeśli
, gdzie
— liczba rzeczywista, to funkcje
,
, liniowo zależne.

Przykład 2.12. Pokaż, że funkcje
są liniowo niezależne przy
.

Równość
jest zwykłym równaniem, które ma trzy pierwiastki, np. spełnia się w pewnych punktach osi
, jeżeli te pierwiastki rzeczywiste. Tym samym tożsamość
sprawiedliwa wtedy i tylko wtedy, kiedy
.

Otrzymany wynik możemy uogólnić na zbiór funkcji
. Wiadomo, że rozwinięcie dowolnej funkcji różniczkowalnej w szereg Taylor'a w otoczeniu punktu
ma postać

.

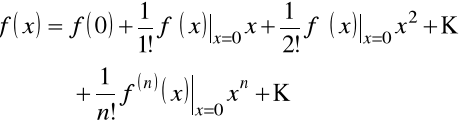
Wówczas możemy mówić o rozwinięciu względem liniowo niezależnych funkcji
, liczba których nieskończona, ale przeliczalna.

Przykład 2.13. Pokaż, że funkcje
są liniowo niezależne przy
, jeśli
różne liczby.

Zapiszemy tożsamość
i załóżmy, że
. Pomnóżmy tożsamość przez
. Otrzymamy

.

Zróżniczkujemy te wyrażenie

.

Pomnóżmy wynik przez
. Mamy

.

Zróżniczkujemy
.

Ponieważ
,
, to mamy sprzeczność. Tym samym tożsamość
sprawiedliwa wtedy i tylko wtedy, kiedy
.

Otrzymany wynik również możemy uogólnić na przypadek przeliczalnej liczby funkcji
, gdzie
są różne liczby.

Wiadomo, że rozwinięcie w szereg Furier'a dowolnej funkcji okresowej ma postać

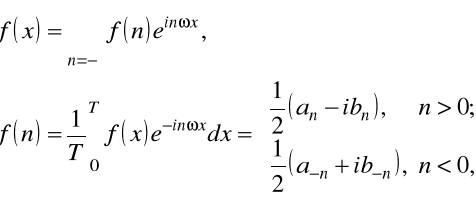
gdzie
— częstotliwość kołowa,
— okres. Oznacza to, że w jakości liczb
wybrano liczby urojone
, gdzie
— liczby całe. Ostatnia równość zapisana z uwzględnieniem wzoru Euler'a

.

Przykład 2.14. Pokaż, że funkcje
są liniowo niezależne przy
, jeśli
liczby rzeczywiste.

Zapiszemy tożsamość
. Ponieważ
, to
. Ale z ostatniego wynika, że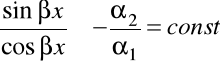
przy
. Co nie odpowiada rzeczywistości - sprzeczność.

Przykład 2.15. Pokaż, że funkcje

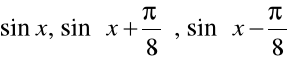
są liniowo zależne przy
.

Złóżmy przeciwne, tzn., że tożsamość

wykonuje się wtedy i tylko wtedy, kiedy
. Jeżeli tak, to mamy kolejno trzy równania jednorodne, na przykład, dla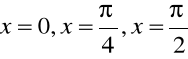
. Mianowicie

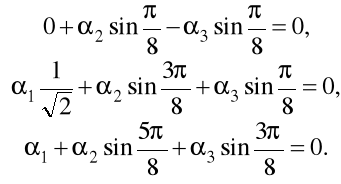
Wyznacznik tego układu równań równia się zero, a rozwiązania nie trywialne będą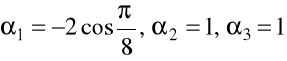
. Wówczas mamy sprzeczność do wyjściowego założenia.

Przykład 2.16. Sprawdzić liniową zależność (niezależność) funkcji
przy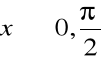
.

Przykład 2.17. Sprawdzić liniową zależność (niezależność) funkcji
przy
.

Definicja 2.2. Dla funkcji
,
, które określone na przedziale otwartym
, zdefiniujemy wyznacznik (wyznacznik Wrońskiego)

.

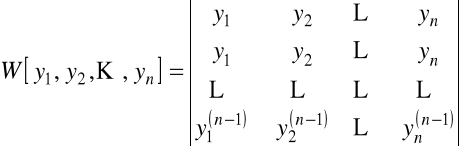
Przykład 2.18. Obliczyć wyznacznik Wrońskiego dla funkcji podanych poprzednich przykładach 2.12-17.

Twierdzenie 2.4. Jeżeli funkcji
,
, które określone na przedziale otwartym
, liniowo zależne, wyznacznik Wrońskiego równia się zero, tzn.
.

Zaznaczmy, że jest to warunek konieczny, ale nie dostateczny. Rozważmy kontrprzykład.

Przykład 2.19. Określimy funkcję

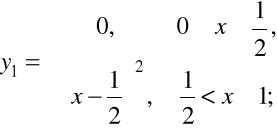
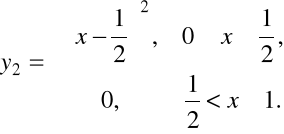
Łatwo sprawdzić, że
, jednak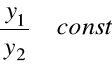
.

Definicja 2.3. Dla funkcji
,
, które określone na przedziale otwartym
, zdefiniujemy wyznacznik (wyznacznik Gramma) wzorem

,

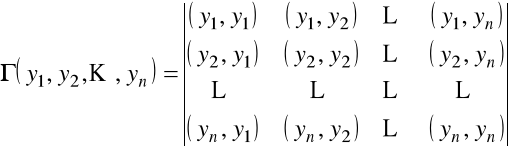
gdzie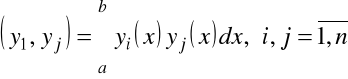
.

Przykład 2.20. Obliczyć wyznacznik Gramma dla funkcji podanych poprzednich przykładach 2.12-17 i 2.19.

Przykład 2.21. Obliczyć wyznacznik Gramma dla funkcji
.

Twierdzenie 2.5. Dla liniowej zależności funkcji
,
, określonych na przedziale otwartym
, koniecznym i dostatecznym warunkiem jest równość do zera wyznacznika Gramma, tzn.
.

1.XXX. Macierzy.

1.4. Przestrzenie metryczne.

Definicja 1.12. Przestrzenią metryczną nazywamy parę (strukturę algebraiczną)
, gdzie
jest zbiorem, a
jest odwzorowaniem zwanym metryką lub odległością

,

dla którego spełnione są warunki

,
,

,

,

Definicja 1.13.

A. Kulą w przestrzeni metrycznej
o środku w punkcie
i o promieniu
nazywamy zbiór punktów
, dla których zachodzi nierówność
.

B. Kulą domkniętą w przestrzeni metrycznej
o środku w punkcie
i o promieniu
nazywamy zbiór punktów
, dla których zachodzi nierówność
.

C. Sferą w przestrzeni metrycznej
o środku w punkcie
i o promieniu
nazywamy zbiór punktów
, dla których zachodzi równość
.

Definicja 1.14 (Granica ciągu). Mówimy, że ciąg ele­mentów
przestrzeni metrycznej
jest zbieżny do elementu
, gdy

.

Definicja 1.15 (Ciąg Cauchy'ego). Mówimy, że ciąg elementów
przestrzeni metrycznej
jest ciągiem Cauchy'ego, gdy

.

Definicja 1.16. Przestrzeń metryczną
nazywamy przestrzenią zupełną, gdy każdy ciąg Cauchy'ego jej elementów jest zbieżny do pewnego elementu
.

Twierdzenie 1.1. Jeśli w jakości zbiory
występuje przestrzeń liniowa
, to działania dodawania i mnożenia powinni być ciągłe, tzn. jeśli w metryce
mamy

oraz
, to

.

Przykład 1.1. Metryka w
może być określona przez wzór

.

Przykład 1.2. Metryka w
może być określona przez wzory

,

,

;

.

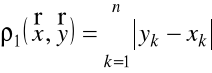
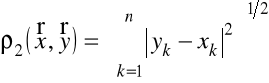
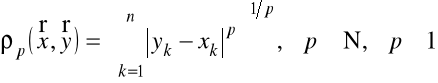
Zaznaczmy, że wtedy powszechnie stosuje się notacji

,
,

,
.

Przykład 1.3. W przestrzeni liniowej ciągów nieskoń­czonych
metryka w może być określona przez wzory

,

,

;

.

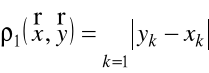
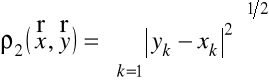
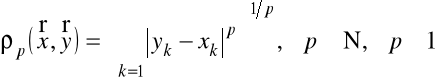
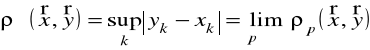
Zaznaczmy, że wtedy odpowiednie przestrzenie liniowe metryczne notuje się

,
,

,
.

Przykład 1.4. W przestrzeni liniowej funkcji rzeczywis­tych ciągłych
lub całkowalnych
określonych w przedziale
różne metryki można wprowadzić następująco

,

,

,

.

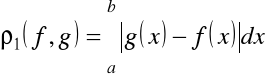
Otrzymamy wtedy następujące przestrzenie metryczne dla funkcji ciągłych

,
,

,

oraz dla funkcji całkowalnych

,
,

.

Zaznaczmy, że przestrzenie
,
,
,
,
,
,
,
są przestrzeniami zupełnymi, natomiast
,
i
nie są zupełne.

Definicja 1.17. Mówimy o metryce z wagą
jeśli (na przykład)

,

,

,

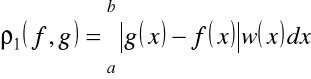
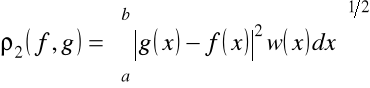
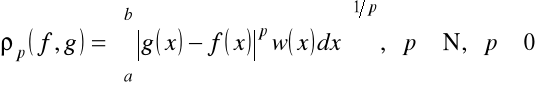
1.5. Przestrzenie unormowane.

Definicja 1.18. Przestrzenią liniową unormowaną nazy­wa się para (struktura algebraiczna)
, gdzie
jest przestrzenią liniową, a
jest odwzorowaniem zwanym normą

,

które spełnia warunki

,
,
,

,
.

Przykład 1.5. Norma w
może być określona przez wzory

,

,

;

.

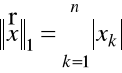
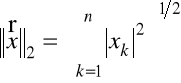
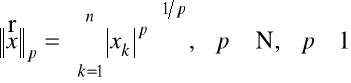
Przykład 1.6. Norma w
może być określona przez wzory

,

,

;

.

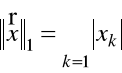
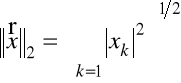
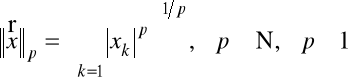
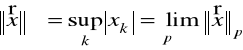
Przykład 1.7. W przestrzeni liniowej funkcji rzeczywis­tych ciągłych
lub całkowalnych
określonych w przedziale
różne normy można wprowadzić następująco

,

,

,

.

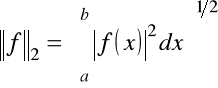
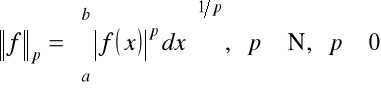
albo normy z wagą

,

,

.

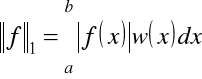
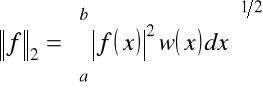
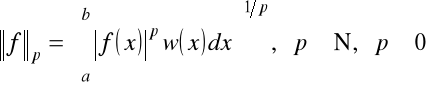
Definicja 1.19. Mówimy o metryce indukowaną przez normę jeśli

.

Definicja 1.20. Dwie przestrzenie unormowane
i
nazywamy izomorficznymi, jeżeli istnieje izomorfizm przestrzeni liniowych
i
, tzn. zachodzi wzajemnie jednoznaczne odwzorowanie
, zachowujące liniowość

i
,

zbieżność ciągów:

jeśli
w metryce indukowanej przez normę
, to
w metryce indukowanej przez normę
.

Definicja 1.21. Przestrzeń unormowana zupełna nazywa się przestrzenią Banacha.

1.6. Przestrzenie liniowe z iloczynem skalarnym.

Definicja 1.22. Przestrzenią liniową z iloczynem skalarnym nazywamy parę (strukturę algebraiczną)
, gdzie
jest przestrzenią liniową, a
jest odwzorowaniem zwanym iloczynem skalarnym

,

które spełnia warunki

,
,

,
,

,
.

Zaznaczmy, że z warunków
i
wynika liniowość iloczynu skalarnego

.

Przykład 1.8. Iloczyn skalarny w
może być określona przez wzór

,

a w przestrzeni
odpowiednio

.

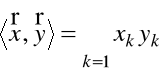
Przykład 1.9. W przestrzeni liniowej funkcji rzeczywis­tych ciągłych
lub całkowalnych
określonych w przedziale
iloczyn skalarny można wprowadzić następująco

,

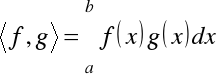
lub z wagą

.

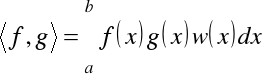
Definicja 1.23. Dwie przestrzenie z iloczynem skalarnym
i
nazywamy izomorficznymi, jeżeli istnieje izomorfizm przestrzeni liniowych
i
, tzn. zachodzi wzajemnie jednoznaczne odwzorowanie
, zachowujące liniowość

i
,

oraz

.

Definicja 1.24. Normą indukowaną przez iloczyn skalar­ny określimy wzorem

.

Definicja 1.25. Nieskończenie wymiarowa przestrzeń liniową z iloczynem skalarnym nazywamy przestrzenią Hilberta, gdy jest ona zupełna w metryce

.

1.7. Układy funkcji ortogonalnych.

Definicja 1.26. Dwie funkcje
i
określone w przedziale
nazywają się ortogonalnymi, jeśli ich iloczyn skalarny jest równy zero, mianowicie

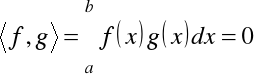
lub iloczyn skalarny z wagą

.

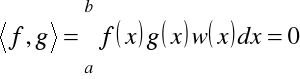
Definicja 1.27. Ciąg skończony

lub nieskończony funkcji

tworzy układ ortogonalny, jeśli

dla
.

Definicja 1.28. Liczbę

nazywamy normą funkcji
w przedziale
.

Definicja 1.29. Jeśli

,

to układ nazywa się układem ortogonalnym.

1.7.A. Układ trygonometryczny

Jest to układ funkcji

,

które są ortogonalne w przedziale
z wagą
i tworzą w tym przedziale przeliczalną bazę przestrzeni
.

1.7.B. Wielomiany Legendre'a
.

Wielomiany tę są rozwiązaniami równania różniczkowego o postaci

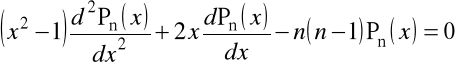
i mogą być definiowane przez wzór Rodrigues'a

,

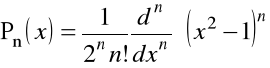
Wielomiany Legendre'a
są ortogonalne w przedziale

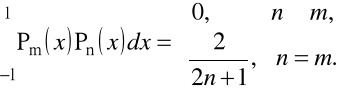
Dla wielomianów Legendre'a
zachodzi równanie rekurencyjne

.

Przykład 1.10. Kilka pierwszych wielomianów Legendre'a
ma postać

,

,

,

,

,

.

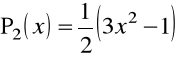
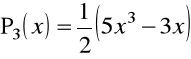
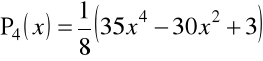
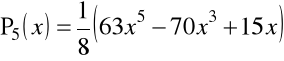
1.7.C. Wielomiany Czebyszev'a pierwszego rodzaju
.

Wielomiany tę są rozwiązaniami równania różniczkowego o postaci

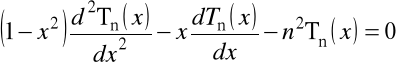
i mogą być definiowane przez wzór Rodrigues'a

,

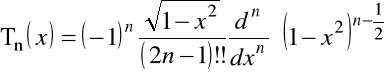
Wielomiany Czebyszev'a
są ortogonalne w przedziale

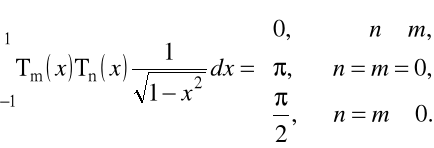
Dla wielomianów Czebyszev'a
zachodzi równanie rekurencyjne

.

Istnieje następujący związek

.

Zera wielomianów Czebyszev'a
pierwszego rodzaju znajdujemy z zależności

,
.

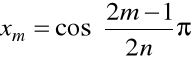
Przykład 1.11. Kilka pierwszych wielomianów Czebyszev'a
ma postać

,

,

,

,

,

.

1.7.D. Wielomiany Laguerre'a
.

Wielomiany tę są rozwiązaniami równania różniczkowego o postaci

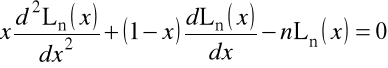
i mogą być definiowane przez wzór Rodrigues'a

,

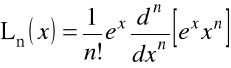
Wielomiany Laguerre'a
są ortogonalne w przedziale

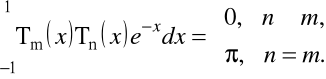
Dla wielomianów Laguerre'a
zachodzi równanie rekurencyjne

.

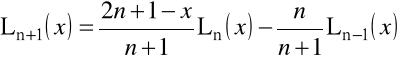
Przykład 1.12. Kilka pierwszych wielomianów Laguerre'a
ma postać

,

,

,

,

,

.

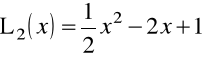
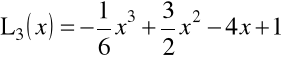
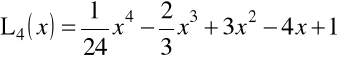
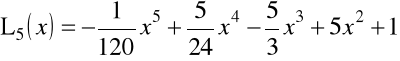
1.7.F. Wielomiany Hermite'a
.

Wielomiany tę są rozwiązaniami równania różniczkowego o postaci

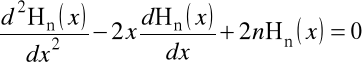
i mogą być definiowane przez wzór

,

Wielomiany Hermite'a
są ortogonalne w przedziale

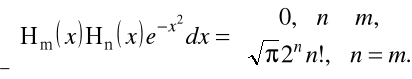
Dla wielomianów Hermite'a
zachodzi równanie rekurencyjne

.

Przykład 1.13. Kilka pierwszych wielomianów Hermite'a
ma postać

,

,

,

,

,

.

---