AKADEMIA GÓRNICZO - HUTNICZA

im. Stanisława Staszica

w Krakowie .

WYDZIAŁ WIERTNICTWA, NAFTY I GAZU

maximum record size = 21570 record size = 1157702386

Laboratorium z Geofizyki Wiertniczej

Temat : Określanie współczynnika porowatości skał .

Wykonali :

Andrzej Jóżwiak,

Robert Myk

III rok WNiG

Specjalność: Wiertnictwo i Geoinżynieria.

Wstęp teoretyczny :

Jedną z wielu fizycznych własności skał jest wielkość zwana stałą dielektryczną - ε. Jest to podatność próbki skalnej na polaryzację zewnętrznym polem elektrycznym, kształtującym wewnętrzną strukturę elektryczną w postaci dipoli. Zjawisko polaryzacji można sobie wyobrazić jako działanie łańcuchów dipolowych formowanych pod wpływem przyłożonego pola zewnętrznego o natężeniu - E_z .

Praktycznie pomiary stałej dielektrycznej prowadzi się przy założeniu niezmienności napięcia między ładunkami powierzchniowymi spolaryzowanej próbki. Dokonuje się tego za pomocą kondensatora zawierającego między okładkami badaną próbkę, którego elektrody zasilane są ze źródła napięcia. Natężenie wewnętrznego pola elektr. próbki jest niezależne od rodzaju wypełniającego kondensator dielektryka. Zewnętrzne natężenie pola zwanego indukcją elektryczną lub przesunięciem elektr. Wynosi :

D = ε⋅ E_w

Bądź też powinno być większe o przyrost natężenia pola pochodzącego od ładunków polaryzacji powierzchniowej P.

D = E_w + 4⋅π⋅P

Polaryzacja P ilościowo jest równa ilorazowi ładunku powierz. Q_p do powierzchni S.

1. Pomiar stałej dielektrycznej próbki skalnej z wielkości powierz. ładunku polaryzacji kondensatora :

Pojemność kondensatora pustego wynosi :

gdzie :

Q_o - ładunek powierzchnowy kondensatora pustego

U - napięcie między okładkami kondensatora

Wprowadzenie między okładki tego kondesatora badanej próbki skalnej powoduje powstanie powierzchniowego ładunku Q_o , który ulega zneutralizowaniu dzięki przepływowi ładunku Q_p zwanego związanym w obwodzie zewnętrznym kondensatora. Pojemnośc kondensatora z dielektrykiem jest powiększona wskutek przyrostu ładunku związanego polarzacji Q_p o wartość ΔC :

lub ε razy od pojemności początkowej C_o :

C_d = ε • C_o

Dla określenia pojemności początkowej w wartości bezwzględnej jest konieczna znajomość powierzchni S okładzin (elektrod ) kondensatora, wzajemnej odległości między okładkami l i wartości bezwzględnej przenikalności powietrza ε_p.:

wartość stałej dielektrycznej powietrza: ε_p = 8,854 • 10^-12 F/m.

2. Opis metody.

Pomiar stałej dielektrycznej próbek skalnych będziemy przeprowadzać przy pomocy kondensatora płaskiego o przekroju kołowym. Pomiędzy okładki tegoż kondensatora wkładamy próbki skalne i odczytujemy wartość pojemności powstałego kondensatora, a następnie prowadzimy pomiar pustego kondensatora. Wartość stałej dielektrycznej danej próbki skalnej obliczamy przy pomocy wzoru:

gdzie:

ε - stała dielektryczna badanej próbki skalnej ,

ΔC - różnica pojemności kondensatora z próbką skalną i kondensatora pustego

l - odległość między okładkami kondensatora ,

S - powierzchnia próbki .

3. Obliczenia :

Lp.	Symbol próbki	Wymiary próbki		Rodzaj pomiaru	Pojemność przy częstotliwości [pF]
					grubość	średnica		1 kHz	10 kHz	100 kHz	1 MHz	10 MHz
		1	30A	12,24	66,5	z próbką	-	203	316	137	99
								b próbki	-	318	376	169	111
ΔC					-	115	60	32	12
2	2	9,84	58,3	z próbką	-	282	355	154	98
								b próbką	-	317	373	167	110
ΔC					-	35	18	13	12

Opracowanie wyników:

Stała dielektryczną obliczamy ze wzoru:

.

Próbka	Stała dielektryczna przy danej częstotliwości[F/cm]				εśr	Δε
	10kHz	100kHz	1MHz	10MHz
30A	5,58	3,39	2,28	1.48	3,18	0,8
2.	2,62	1,83	1,6	1,55	1,9	0,8

Błąd pomiaru stałej dielektrycznej obliczamy za pomocą różniczki zupełnej:

∆ є=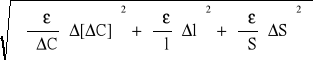

ΔC = 1pF

Δl = 0,1cm

ΔS = 0,01cm²

Wnioski:

W przeprowadzonym ćwiczeniu dokonaliśmy pomiaru stałej dielektrycznej skał za pomocą E- metru Pomiar sprowadzał się do określenia pojemności kondensatora pustego a następnie pojemności kondensatora z badaną próbką. Znając zmianę pojemności oraz wymiary próbki skalnej ze wzoru mogliśmy określić stałą dielektryczną. Z uzyskanych wyników możemy wnioskować o zależności między stałą dielektryczną a częstotliwością pola polaryzującego . Im większa częstotliwość tym mniejsza stała dielektryczna próbki.

U=E_w·l

-P

gęstość łądunków

polaryzacji na

powierzchni próbki

gęstość ładunków

na okładce

l

+++++++++++

___________

E_W

P

---