1. Podstawowe pojęcia mechaniki. Modele ciał rzeczywistych.

Modele ciał rzeczywistych:

• Punktem materialnym nazywamy model ciała o tak małych wymiarach w porównaniu z wymiarami obszaru, w którym ciało porusza się, że można pominąć zmiany położenia tego ciała wywołane przez obrót i traktować to ciało jako punkt geometryczny, któremu przypisujemy przy tym pewną skończona ilość materii.

• Ciało doskonale sztywne to wyidealizowane ciało stałe, którego punkty nie zmieniają wzajemnych odległości. Ciało to nie podlega, więc żadnym odkształceniom pod wpływem sił na nie działających. Ciało rzeczywiste można z wystarczającym przybliżeniem traktować jako ciało doskonale sztywne wówczas, gdy ich odkształcenia są pomijalnie małe.

• Rachunek wektorowy. Dodawanie wektorów.

• Zasada równoległoboku- dwie dowolne siły P1i P2, przyłożone do jednego punktu, zastąpić możemy siłą wypadkową R przyłożoną do tegoż punktu i przedstawioną jako wektor będący przekątną równoległoboku rozpiętego na wektorach P1 i P2




-kąt między P1 i P2

3. Iloczyn wektorowy i skalarny.

• Iloczyn skalarny
  

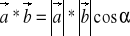
• Iloczyn wektorowy
  
  

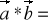
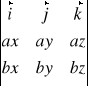
• Rzut wektora na oś.

• Rzut siły F na oś l Fl=F*cos
  
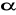
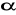
  -kąt między siłą F a osią l

5. Moment wektora względem punktu i względem osi.

• Analogicznie do momentu siły (patrz niżej)

6. Podstawy i zadania mechaniki. Modelowanie w mechanice. Ruch i spoczynek

7. Stopnie swobody układu. Więzy-podparcia bryły sztywnej

• Stopień swobody układu : dla punktu materialnego: na płaszczyźnie s=2n-w; w przestrzeni s=3n-w; dla bryły s=6n-w; dla tarczy s=3n-w

• Więzy

1. Podpora przegubowa nieprzesuwna( dwie siły-pionowa i pozioma)

2. Podpora przegubowa przesuwna( jedna sił pionowa)

3. Utwierdzenie(dwie siły-pionowa i pozioma oraz moment siły)

Statyka

1. Siła. Układy sił.

• W mechanice siły określamy ogólnie jako wzajemne oddziaływanie ciał na siebie. Oddziaływania te przewijają się bądź to przez wyprowadzenie ciał ze stanu spoczynku, bądź to przez zmianę ruchu poruszających się już ciał.

• Załóżmy, że do pewnego ciała sztywnego przyłożone są siły, których linie działania leżą w jednej płaszczyźnie i przecinają się wszystkie w jednym punkcie. Taki układ sił nazywamy płaskim układem sił zbieżnych.

• Aksjomaty statyki.

Prawa Newtona:

• Pierwsze prawo-Punkt materialny, na który nie działa żadna siła, pozostaje w spoczynku lub porusza się ruchem jednostajnym po linii prostej.

• Drugie prawo-Przyspieszenie punktu materialnego jest proporcjonalne do siły działającej na ten punkt i ma kierunek siły.

• Trzecie prawo-Siły wzajemnego oddziaływania dwóch punktów materialnych są równe, co do wartości i są przeciwnie skierowane wzdłuż prostej łączącej oba punkty.

Drugi aksjomat

• Jeśli mamy układ sił zaczepionych w jednym punkcie to można go zastąpić jedną siłą wypadkową W=F1+F2+F3…+Fn

Trzeci aksjomat

• Dwie siły przyłożone do ciała sztywnego równoważą się tylko wtedy, gdy działają wzdłuż jednej prostej, są przeciwnie skierowane i mają te same wartości liczbowe.

Czwarty aksjomat

• Zasada działania i przeciwdziałania. Każdemu działaniu towarzyszy równe, co do wartości i przeciwnie skierowane wzdłuż tej samej prostej przeciwdziałanie.

Piąty aksjomat

• Obciążenie jest siłą czynną a siła w linach jest siłą bierną. Każde ciało nieswobodne można oswobodzić z więzów i rozpatrywać to ciało jako swobodne

3. Moment siły względem punktu

• Ramieniem siły P względem dowolnie obranego punktu O nazywamy odległość h linii działania tej siły od punktu O. Z określenia tego wynika, że ramię siły względem punktu jest równe zeru wtedy, gdy linia działania siły przechodzi przez dany punkt.

• Momentem siły względem punktu O nazwiemy wektor, którego wartość bezwzględna równa jest iloczynowi wartości liczbowej siły P i ramienia tej siły względem punktu O. Wektor ten, który oznaczymy przez Mo, poprowadzimy z punktu O prostopadle do płaszczyzny wyznaczonej przez linię działania siły oraz punkt O i skierujemy w ten sposób, aby dla obserwatora patrzącego z jego końca na tę płaszczyznę, kierunek obrotu, który siła P stara się wywołać względem punktu O, był przeciwny do kierunku ruchu wskazówek zegara.

Mo=h*P

4. Moment siły względem osi(str152 Leyko)

• Moment siły względem osi określamy w następujący sposób. Niech będzie dana siła P przyłożona w punkcie A oraz oś, którą oznaczymy przez z. Przez dowolny punkt O osi z przeprowadzimy płaszczyznę
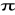
  prostopadłą do tej osi. Następnie rzutujemy siłę P na tą płaszczyznę otrzymując rzut P' danej siły. Momentem siły P względem osi z nazwiemy moment rzutu P' danej siły na płaszczyznę prostopadłą do tej osi względem punktu O, w którym oś z przebija wspomnianą płaszczyznę.

Mz=
P'h'

5. Para sił - (str 67 Leyko)dwie równoległe siły przeciwnie skierowane i równe co do wartości. Siły takie nie maja wypadkowej, ale i nie równoważą się, gdyż nie działają wzdłuż jednej prostej. Para sił działając na ciało materialne wywołuje jego obrót. Odległość a między liniami działania sił tworzących parę nazywamy ramieniem pary sił. Moment pary sił to iloczyn ramienia tej pary sił oraz wartości jednej z tych sił.




6. Redukcja ogólnego układu sił (str162 Leyko)

• Dowolny układ sił działających na ciało sztywne zastąpić możemy siłą R przyłożoną do dowolnie wybranego środka redukcji O, równą sumie geometrycznej wszystkich sił układu, oraz parą sił o momencie Mo, równym sumie geometrycznej momentów tych sił względem środka O. Siłę R nazywamy wektorem głównym, moment Mo zaś momentem głównym.

• Warunki równowagi ogólnego układu sił(str165Leyko)

• W ogólnym przypadku sił działających na ciało sztywne równowaga możliwa jest tylko wtedy, gdy suma geometryczna tych sił równa jest zeru oraz gdy suma geometryczna ich momentów względem dowolnego punktu O jest także równa zeru.


;
;
;
;
;
;

8. Warunki równowagi układu sił równoległych

• Gdy obierzemy prostokątny układ współrzędnych Oxyz w taki sposób, aby oś Oz była równoległa do linii działania rozpatrywanych tu sił, wówczas równania rzutów na osie x i y będą spełnione tożsamościowo, gdyż rzuty wszystkich sił na te osie są równe zeru. Podobnie będzie spełnione równanie momentów względem osi z ponieważ wszystkie siły są równoległe do tej osi. Z ogólnych sześciu równań równowagi pozostają trzy:


;
;
;

9. Warunki równowagi zbieżnego układu sił

• 
  ;
  ;
  

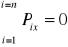
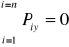
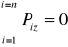
10. Warunki równowagi płaskiego układu sił

• Aby dowolny układ sił o liniach działania leżących w jednej płaszczyźnie był w równowadze, suma geometryczna tych sił oraz suma algebraiczna ich momentów względem dowolnie obranego punktu tej płaszczyzny muszą być równe zeru.


;
;
;

11. Obliczenia reakcji więzów w płaskim układzie tarcz(belek i ram)

12. Warunki statycznej wyznaczalności i geometrycznej niezmienności układu

• Belka Gerbera.

1. Stopień statycznej niewyznaczalności musi być równy 0 ns=r-3-p=0 r- liczna reakcji w belce p- liczba przegubów

2. Geometryczna niezmienność p<2w-3

• Rama

1. Stopień statycznej niewyznaczalności ns=r+3z-p-3 r- reakcje, z- liczba zamkniętych obwodów, p - liczba przegubów pojedynczych

• Kratownica

1. Stopień statycznej niewyznaczalności ns=r+p-2w r- reakcje, p- pręty, w- węzły

2. Geometryczna niezmienność p>2w-3(kratownica płaska) p>3w-6 (kratownica przestrzenna) p- liczba prętów, w- liczba węzłów.

13. Definicja sił wewnętrznych w konstrukcjach prętowych

• Siły wewnętrzne stanowią oddziaływania między poszczególnymi elementami ciała. Siły wewnętrzne są zawsze parami przeciwne, mają równe wartości i działają wzdłuż tej samej prostej. W celu ujawnienia tych sił stosuje się metodę przecięć, która polega na myślowym przecięciu ciała dowolną płaszczyzną.

• Siły wewnętrzne w konstrukcjach kratowych

• Analiza statyczna i kinematyczna kratownic

• Metoda zrównoważenia węzłów dla kratownic

• Metoda Rittera dla kratownic

• Tarcie ślizgowe. Tarcie toczenia(str98 Leyko)

Kinematyka

1. Kinematyka punktu materialnego. Sposoby opisu ruchu.(str214 Leyko)

• Równania ruchu punktu x=f1(t); y=f2(t); z=f3(t) - za pomocą tych równań możemy dla dowolnej wartości czasu, czyli dla dowolnej chwili, wyznaczyć współrzędne punktu A, czyli tym samym możemy określić chwilowe jego położenie.

• Poruszający się w przestrzeni punkt A opisuje w przestrzeni pewna linię, będącą miejscem geometrycznym chwilowych jego położeń. Linię tę, nazywamy torem ruchu. Gdy torem badanego punktu jest linia płaska, możemy wówczas tak obrać nieruchomy układ współrzędnych, aby jego osie Ox i Oy leżały w płaszczyźnie tej linii. W tym przypadku mamy równania ruchu x=f1(t); y=f2(t); Po wyrugowaniu z tych równań czasu t otrzymujemy równanie toru ruchu o ogólnej postaci f(x,y)=0. Gdy punkt A porusza się po linii prostej to prosta tą obieramy jako oś Prędkość, wówczas mamy tylko jedno równanie ruchu: x=f1(t);

• W przypadku, gdy punkt A porusza się, jego promień-wektor r zmienia z upływem czasu swą wartość i kierunek, czyli zależy od czasu t. Mówimy wtedy, że promień-wektor jest pewną funkcją wektorową czasu i zaznaczamy to w następujący sposób r=r(t)

• Prędkość punktu materialnego(str223Leyko)

• Prędkością punktu poruszającego się ruchem prostoliniowym i jednostajnym nazwiemy wektor v, którego wartość bezwzględna równa jest bezwzględnej wartości stosunku
  


(
)
-przyrost, którego doznaje odcięta x


- zmiana czasu

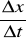
• Ruch harmoniczny vx=akcos(kt+
  )

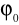
3. Przyspieszenie punktu materialnego

• Przyspieszeniem średnim punktu materialnego jest zmiana prędkości tego punktu w czasie Pśr=
  

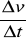
• Aby wyznaczyć wielkość, która charakteryzuje zmianę prędkości w danej chwili, należy we wzorze przejść do granicy zakładając, że
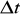
  dąży do zera. Wektor do którego dąży wówczas przyspieszenie średnie nazywamy przyspieszeniem w chwili t. P=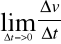
  
  
  z czego wynika p=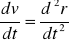
  

• Ruch harmoniczny px= -ak
  

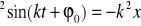
4. Ruch postępowy bryły materialnej

• Załóżmy, że ciało sztywne porusza się w ten sposób, że dowolna prosta należąca do tego ciała pozostaje stale równoległa do swego położenia, które zajmowała w pewnej dowolnie obranej chwili, np. w chwili początkowej. Tego rodzaju ruch ciała nazywamy ruchem postępowym. W ruchu tym przesunięcia wszystkich punktów ciała sztywnego są takie same.

5. Ruch obrotowy bryły względem stałej osi.

• Rozważmy ciało sztywne, którego jedna prosta została unieruchomiona, w tym wypadku ciało może jedynie obracać się wokół tej osi, która nosi nazwę osi obrotu. Ruch, który może wykonywać rozpatrywane ciało sztywne nazywamy ruchem obrotowym. Torami punktów ciała są koła położone w płaszczyznach prostopadłych do osi obrotu i środkach leżących na tej osi. Gdy ciało sztywne porusza się wokół osi, wówczas kąt obrotu jest pewna funkcją czasu.




6. Prędkość kątowa punktów bryły w ruchu obrotowym

• Załóżmy, że od chwili t do chwili t1=t+
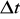
  , kąt obrotu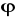
  doznał przyrostu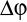
  czyli osiągnął wartość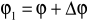
  . Stosunek przyrostu kąta obrotu do odpowiedniego przyrostu czasu nazwiemy średnią prędkością kątową ciała. Oznaczając tę prędkość przez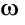
  , mamy, więc:


=


prędkość kątowa w chwili t równa jest:


7. Przyspieszenie obrotowe punktów bryły w ruchu obrotowym

• Przyspieszeniem kątowym nazywamy wzrost prędkości kątowej w czasie. Średnie przyspieszenie kątowe określone jest następującym wzorem:




Aby otrzymać przyspieszenie w danej chwili t, należy przejść do granicy, zakładając, że
->0 :




8. Ruch płaski bryły

9. Centroida ruchoma i nieruchoma

10. Stopnie swobody układu tarcz

11. Kinematyka i plan biegunów układu tarcz

Dynamika

1. Podstawy dynamiki. Prawa Newtona.

2. Pole sił. Energia potencjalna. Praca i moc

3. Dynamika punktu i ciała. Pęd i kręt

4. Energia kinetyczna układu punktów materialnych

5. Równania różniczkowe ruchu punktu swobodnego. Typ zadań w dynamice.

6. Równania różniczkowe ruchu punktu nieswobodnego.

7. Ogólne równanie dynamiki

8. Podstawy mechaniki analitycznej. Więzy i ich klasyfikacja

9. Przemieszczenia wirtualne. Więzy idealne.

10. Równania różniczkowe ruchu punktu nieswobodnego

11. Zasada prac(przemieszczeń)wirtualnych

12. Wykorzystanie zasady prac wirtualnych do obliczenia reakcji

13. Zasada d'Alemberta

14. Siły i przemieszczenia uogólnione

15. Drgania swobodne. Ruch harmoniczny-okres i częstotliwość.

16. Drgania wymuszone harmonicznie. Zjawisko rezonansu.