POLITECHNIKA ZIELONOGÓRSKA
WYDZIAŁ BUDOWNICTWA I INŻYNIERII SANITARNEJ
PRACOWNIA FIZYKI
FIZYKA
„Teoria błędów”
Maciej Lutowski, gr. 13
Rok akademicki 2000/01
Przy wszelkich pracach doświadczalnych z dziedziny fizyki spotykamy się z dwoma następującymi po sobie procesami:
z pomiarami, które przeprowadza się za pomocą specjalnych przyrządów
z obliczeniami, tj. matematycznym opracowaniem wyników pomiarów
Zadaniem matematycznego opracowania wyników pomiarów jest również ich krytyczna analiza, która mogłaby dać ocenę prawidłowości pomiarów i stopień ich pewności. Wskutek niedoskonałości przyrządów pomiarowych, którymi się posługujemy, jak również wskutek niedoskonałości organów zmysłów biorących udział w obserwacjach, wszystkie pomiary mogą być dokonywane z pewnym określonym stopniem dokładności. Z tego względu wyniki pomiarów nie dają nam prawidłowych wartości mierzonej wartości, lecz wartości do niej zbliżone. Wszystkie przybliżone wartości wielkości fizycznych obarczone więc są pewnym błędem, który przyjęto określać jako:
błąd bezwzględny (absolutny)
błąd względny.
2. Błąd bezwzględny
Błędem bezwzględnym jakiegoś pomiaru nazywam różnicę między dokładną wartością rzeczywistą, a jej wartością przybliżoną:
ε = X - A
gdzie:
ε - bezwzględny błąd pomiaru
X - prawdziwa dokładna wartość mierzonej wielkości
A - wartość przybliżona otrzymana drogą pomiaru
Stąd mamy:
X = A + ε
A więc dokładną wartość danej wielkości znajdujemy przez zsumowanie wartości przybliżonej i jej błędu.
3. Błąd względny
Błędem względnym danej wielkości nazywamy stosunek błędu bezwzględnego do prawdziwej wartości poszukiwanej wielkości:
![]()
gdzie:
δ - błąd względny
Wielkość X w powyższych równaniach nie jest nam znana, stąd wniosek, że dokładnej wartości zarówno ε jak i δ określić nie możemy. Jeżeli założymy, że błąd bezwzględny ε jest wielkością małą w porównaniu z X czy A, to można przyjąć, że są one blisko siebie. Można zastąpić więc X przez A:
![]()
ε = δA
gdzie: δ << 1 i δ = 100 δ %
Przy starannie wykonanych pomiarach ich błędy bezwzględne nie powinny przekraczać tzw. dokładności pomiarów, tj. najmniejszej wielkości, jaką możemy odczytać posługując się danym przyrządem. Jednak dokładność pomiaru błędu tym sposobem jest mała.
4. Znak błędów wielkości przybliżonych
Przy dokonywaniu pomiarów nigdy nie możemy określić, czy popełniamy błąd w kierunku powiększania czy tez pomniejszania badanej wartości. Zatem błędy wielkości przybliżonych są albo dodatnie albo ujemne. Okoliczność ta w teorii błędów odgrywa bardzo ważną rolę.
|
|
|
Różnice między błędem bezwzględnym i względnym pozwalają uczynić następujące uwagi:
Błędy bezwzględne są wielkościami mianowanymi, tak jak i wielkości, do których się odnoszą
Błędy względne są wielkościami niemianowanymi. Dzięki temu można porównywać dokładność pomiarów wielkości różnorodnych, np. pomiarów mas, czasu, długości. Takie porównanie dokładności różnych pomiarów spotyka się często w praktyce.
Oba błędy zależą od dokładności pomiarów, jednak błąd ε zależy oprócz tego od wartości mierzonej wielkości. Możemy więc otrzymać różne błędy względne przy tym samym błędzie bezwzględnym.
Bardziej przejrzystym wskaźnikiem dokładności jest błąd względny
Klasyfikacja wielkości przybliżonych
Wartości przybliżone możemy podzielić na trzy grupy:
Wartości stałych matematycznych. Traktujemy je jako wartości stałe, nie obarczone błędami
Wielkości stałych fizycznych. Je także uważamy za pozbawione błędu
Wyniki zwykłych pomiarów fizycznych w laboratorium. Przyczyny ich powstawania także możemy podzielić na trzy grupy:
błędy systematyczne - wynikające z niedokładności przyrządów, błędnej metody pomiarów lub z działania czynników zewnętrznych.
błędy grube - powstające wskutek fałszywego odczytania przyrządów lub nieprawidłowego zapisania.
błędy przypadkowe - popełniane przy nastawianiu przyrządów i ich odczytywaniu.
Nie ograniczamy się więc do jednego wykonania pomiaru, lecz powtarzamy czynność kilkakrotnie, nie sugerując się pierwszym otrzymanym wynikiem. Teoria błędów stosuje się tylko do błędów przypadkowych.
Prawo normalnego rozkładu błędów przypadkowych
Występowanie błędów przypadkowych podlega pewnej prawidłowości. Błędy małe pojawiają się w większej liczbie, duże rzadziej. Zależność występowania błędu od jego wartości określa prawo Gaussa:
![]()
gdzie:
x - wartość błędu
y(x) - częstość występowania błędu (gęstość prawdopodobieństwa)
h - liczba stała, (współczynnik dokładności pomiarów)
Wykresem tej funkcji jest krzywa, symetryczna względem osi y:
Występująca w równaniu Gaussa stała doświadczalna h decyduje o tym, czy krzywa jest więcej czy mniej stroma. Jest ona tym większa, im dokładniejszy jest przyrząd.
Łącząc pojęcia prawdopodobieństwa błędu z ogólną liczbą N wykonanych pomiarów mamy:
![]()
Mając dane N oraz rozkład błędów wyrażony równaniem Gaussa można zawsze na podstawie tego równania wyznaczyć liczbę błędów n zawartych w danym przedziale.
Postulat średniej arytmetycznej pomiarów
Przy pomiarach jednakowej dokładności najbardziej prawdopodobną wartością mierzonej wielkości jest średnia arytmetyczna wszystkich otrzymanych wyników pomiarów, określona wzorem:
![]()
Wprowadzając postulat średniej arytmetycznej, oznaczonej przez A, otrzymujemy dwa szeregi równań:
Dla dokładnej wartości błędu
|
Dla odstępstw od średniej arytmetycznej |
...................
|
..................
|
gdzie:
εn - błędy liczone w stosunku do średniej arytmetycznej pomiarów
Dla odstępstw ε istnieje prawo analogiczne do prawa Gaussa:
![]()
gdzie:
![]()
n - liczba pomiarów, na podstawie których została wyznaczona średnia arytmetyczna A
Przy dużej liczbie pomiarów średnia arytmetyczna otrzymanych wyników jest bardzo bliska dokładnej wartości wielkości mierzonej
Wskaźniki dokładności pomiarów
Przyjęto stosowanie trzech następującch wskaźników dokładności pomiarów:
błąd średni kwadratowy , określony wzorem (wielkość znajdująca się po prawej stronie):
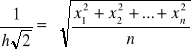
błąd prawdopodobny r:
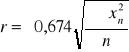
błąd przeciętny x0:
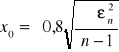
Graficzne przedstawienie wyników pomiarów. Metoda różniczki zupełnej i pochodnej logarytmicznej
Gdy mamy dwie wielkości fizyczne y i x związane z wielkością funkcjonalną y=f(x) stosujemy często graficzne przedstawienie tej zależności. Obrazem graficznym posługujemy się wtedy, gdy drogą doświadczalną otrzymujemy szereg odpowiadających im wartości wielkości y. Zestawiamy dane w postaci par x i y i na ich podstawie wykonujemy wykres.
Metoda różniczki zupełnej
![]()
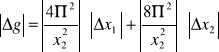
Metoda pochodnej logarytmicznej
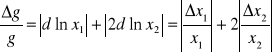
![]()
Wyszukiwarka
Podobne podstrony:
1222
1222
1222
1222
Dz.U.2009.152.1222 Substancje i prep. chemiczne, BHP, Akty prawne
Instalacja elektryczna Ursus 912 914 1012 1014 1222 1224 1614 1929
1222
1222
Ursus 912, 914, 1012, 1014, 1222, 1224, 1614, kabina kierowcy
1222
Jak podłączyć wskaźnik poziomu paliwa w URSUSIE C 385 902 904 912 914 1002 1004 1012 1014 1212 1214
Ursus 1222, 1224, 1614
Instalacja elektryczna Ursus 912 914 1012 1014 1222 1224 1614 1929
Jak podłączyć wskaźnik poziomu paliwa w URSUSIE C 385 902 904 912 914 1002 1004 1012 1014 1212 1214
więcej podobnych podstron