Stan układu: wyróżnia się dwa stany: czysty: występuje wtedy, gdy charakteryzujące stany układu kwantowego liczby kwantowe są jednoznacznie określone. Stan taki jest opisywany jedną funkcją falową Ψ, a wartość średnia dowolnej wielkości fizycznej układu ujmowanej przez hermitowski operator A może być obliczona na podstawie wzoru:
. Mieszany: to stan układu kwantowego będący sumą nieskończenie wielu stanów czystych, przy czym prawdopodobieństwo udziału każdego z tych ostatnich w stanie mieszanym określone jest przez tzw. Macierz gęstości. Stanu tego nie opisuje jedna funkcja falowa, a wielkości układu przyjmują wartości nie będące wartościami własnymi odpowiadających im operatorów. Ze względu na energię stanu układu wyróżnia się stan podstawowy i wzbudzony.

Funkcja falowa: podstawowa wielkość opisująca stan układu kwantowego (położenie cząstki w przestrzeni) w ujęciu nie relatywistycznym lub w prostych układach relatywistycznych, np.: cząstka swobodna lub w słabym polu. Opis ma charakter probabilistyczny, kwadrat modułu f.f. dla danych wartości zmiennych określa prawdopodobieństw

znalezienia tego układu w stanie określonym przez te zmienne. F.f. jest dana funkcją zespoloną, określoną z dokładno

do fazy. W ujeciu nierelaty. spełnia równanie Schrodingera, w relaty. np. równanie Diraca. (ele. przest. Hilberta)

Zasada superpozycji: Jeżeli wektory |Ψ­₁> i |Ψ₂> określają możliwe stany tego samego układu, to możliwy stan tego układu jest także określany przez wektor: |Ψ>=C₁|Ψ₁> + C₂|Ψ₁>.

Interpretacja probabilistyczna Ψ: Funkcja falowa Ψ(r,t) opisuje falę prawdopodobieństwa. Wielkość Ψ*(r,t)Ψ(r,t) jest gęstością prawdopodobieństwa znalezienia cząstki w punkcie r w chwili t. Całka z powyższego po całym obszarze D jest prawdopodobieństwem znalezienia cząstki w chwili t w D. Równanie ciągłości

interpretujemy zatem jako lokalne prawo zachowania prawdopodobieństwa, a przez j(r,t) rozumiemy gęstość prądu prawdopodobieństwa . Prawdopodobieństwo nie może się pojawiać ani znikać, może się ono jedynie przemieszczać. Całkowite prawdopodobieństwo znalezienia cząstki jest równe jedności, jeżeli spełniony jest warunek unormowania. Jeżeli Ψ=∑c_nΨ_n, z warunków unormowania i ortonormalności wynika, że: ∑|C_n|² =1. Zatem |C_n|² można zinterpretować jako prawdopodobieństwo występowania układu w stanie Ψ_n. (1926, +28 Nobel).

Kot, który przenika ściany: W szczelnie zamkniętym pokoju zamykamy żywego kota, po czym zachodzi proces, który zgodnie z prawami mechaniki kwantowej doprowadza do superpozycji dwóch równie prawdopodobnych stanó

W jednym z nich kot jest żywy, a w drugim martwy. Po zajściu owego procesu kot jest połowicznie żywy, połowiczn

martwy. Jednak zaglądając do pokoju widzimy kota albo całkowicie żywego, albo całkowicie martwego. Należy zastanowić się co zabiło/pozwoliło żyć kota/u. Nie był to pomiar stanu kota, ale interpretacja probabilistyczna. Schre

chciał zobrazować sprzeczność wyników proponowanych przez interpretacje probabilistyczną z wynikami proponow

przez zdrowy rozsądek. Zwolennicy wyjaśniają, że teoria zakłada prowadzenie doświadczenie na wielu podobnych kotach, a wynik mówi, że w połowie przypadków kot by przeżył.

Opis stanów kwantowych w formalizmie wektorowym: Amplitudę prawdopodobieństwa zapisujemy: < x | s >. Kiedy cząstka może osiągnąć dany stan dwiema drogami, całkowita amplituda prawd. Dla tego procesu jest sumą amplitud dla procesów odpowiadających przejściu cząstki po każdej z tych dróg z osobna: <x|s>=<x|s>₁+<x|s>_2. W wypadku, gdy cząstka porusza się po określonej drodze, odpowiednia amplituda prawd. Może być zapisana jako iloczyn amplitudy przebycia części drogi i amplitudy przejścia pozostałej drogi, <x|s>_{przez 1}=<x|1> <1|s>. Dla wielu szczelin: <x|s>=∑<x|a> <a|i> <i|s>; a=a,b,c...;i=1,2...

Operatory: ogólna nazwa dla przekształcenia przeprowadzającego jeden zbiór w drugi. Wielkością fizycznym, obserwablom, przypisuje się odpowiadające im operatory różniczkowe, np. pędu=-ih∇, energii=ihδ/δt, przypisanie takie można uzasadnić na podstawie przekształcenia Laplace`a. Op. Inwersji: I f(x)=f(-x), transmisji: T_af(x)=f(x+a),

Własności: Cf=Af+Bf;Cf=ABf=Ag ; Bf=g, (A+B)Cf=ACf+BCf, (AB)Cf=A(BC)f, BB=B²f, B^n-1Bf=Bⁿf, (AB)^-1=A^-1 B^-1, ABf≠Baf.

Iloczyn hermitowski: iloczyn hermitowski wewnętrzny: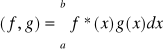
, własności: (f,g,h funkcje ciągłe) (g,f)=(f,g)*, (f,g+h)=(f,g)+(f,h),(f+h,g)=(f,g)+(h,g), (af,g)=a*(f,g),(f,ag)=a(f,g),(f,f)=0, TW: (f,f)=0 ⇔ gdy f(x)≡0, if (g,f)=0 then f(x)=0, if (f,g)=(f,h) then g(x)=h(x).

Nierówność Szwartza: Teza: |(f,g)|²<=(f,f)(g,g) Dowód: (h,h)≥0,h=f+ag; a*= - (g,f)*/(g,g)*, a= - (g,f)/(g,g); (h,h)=(f+ag,f+ag)=(f,f)+(f,ag)+(ag,f)+(ag,ag)=(f,f)+a(f,g)+a*(g,f)+a*a(g,g)≥0 // razy (g,g) //, (f,f)(g,g)+a(f,g)(g,g)+ a*(g,f)(g,g)+ a*(g,f)(g,g) + a*a(g,g)(g,g)≥0, // podst a i a* // (f,f)(g,g) - (g,f)(f,g)-( (g,f)*/(g,g)* )(g,f)(g,g) + ( ( (g,f)*(g,f) ) / (g,g)* )(g,g)≥0, (f,f)(g,g) - (g,f)(f,g)≥0, (f,f)(g,g)-(f,g)*(f,g)≥0, (f,f)(g,g)≥(f,g)*(f,g), (f,f)(g,g)≥|(f,g)|²

Operatory hermitowskie...Operator jest hermitowski gdy: SΨ₁*LΨ₂dv=S(LΨ₁)*Ψ₂dv własości: (a+b)^t=a^t+b^t, (za)^t=z*a^t, (ab)^t=b^ta^t,(a^t)^t=a, gdzie a^t=(a^T)*, wart. wl. ∈R : a∈R gdy a=a*, wiedzac ze: SΨ₁*AΨ₂dx=SΨ₂A*Ψ₁*dx, AΨ=aΨ, (AΨ)*=(aΨ)*, A*Ψ*=a*Ψ*,SΨ*Ψdx=1, Dowod: AΨ=aΨ, Ψ*AΨ=Ψ*aΨ, SΨ*AΨdx=SΨ*aΨdx=aSΨ*Ψdx=a, analogicznie: A*Ψ*=a*Ψ*, ΨA*Ψ*=Ψa*Ψ*, SΨA*Ψ*dx=a*SΨΨ*dx, SΨA*Ψ*dx=a*, SΨ*AΨdx=SΨA*Ψdx, a=a*, a∈R. Udow. Wiedząc: SΨ₁*AΨ₂dx= SΨ₂A*Ψ₁*dx, a₁≠a₂∈R, SΨ₁*Ψ₂dx=SΨ₂*Ψ₁dx=0 Dowod:AΨ₁=a₁Ψ_1, Ψ₂*AΨ₁=Ψ₂*a₁Ψ₁,SΨ₂*AΨ₁dx=a₂S Ψ₂*Ψ₁dx

AΨ₂=a₂Ψ₂, Ψ₁*AΨ₂=Ψ₁*a₂Ψ₂, SΨ₁*AΨ₂dx= SΨ₁*a₂Ψ₂dx, SΨ₁A*Ψ₂ *dx= a₂ SΨ₁Ψ₂* dx, SΨ₂*AΨ₁dx=a₂SΨ₂*Ψ₁

a₁SΨ₂*Ψ₁dx=a₂SΨ₂*Ψ₁dx, (a₁-a₂)SΨ₂*Ψ₁dx=0, SΨ₂*Ψ₁dx=0 gdyz a₁≠a₂.

Zagadnienie własne: Operatot jest liniowy gdy dla dowolnych funkcji u oraz stałych α zachodzi: L(α₁u₁+α₂u₂)=α₁Lu₁+α₂Lu₂. Zagadnienie własne to problem znalezienia wektora własnego i wartości własnej właściwych danej macierzy A lub operatorowi O, takich że: Af=af, Of=af. Funkcja musi być: jednoznaczna,ciągła, różna od zera, ograniczona, całkowalna z kwadratem. Zbiór wszystkich wartości własnych danego operatora tworzy widmo(dyskretne, ciągłe lub mieszane). Jeżeli danej wartości własnej może odpowiadać wiele funkcji własnych mówimy o degeneracji. Wartości własne operatorów hermitowskich są rzeczywiste. Dwie funkcje własne operatorów hermitowskich odpowiadają różnym wartością włas nym (są ortogonalne).Jeżeli dwa operatory mają identyczny układ funkcji własnych to komutują ze sobą.

Reprezentacja macierzowa... AΨ_j: Ψ_j=∑Cn_jf_n; f_n:funkcje bazy; AΨ_j=A(∑Cn_jf_n)=∑Cn_jAf_n; Af_n=∑a_knf_n; a_kn=(f_k,Af_n) Jeżeli bazą jest ortonormalny układ funkcji własnych odpowiadający wartością własnym α_k to macierz odpowiadająca operatorowi będzie diagonalna. [a_kn=α_kδ_kn]. Reprezentacje macierzowe dwóch operatorów w tym samym układzie zupełnym są identyczne wtedy i tylko wtedy gdy te operatory są sobie równe. Reprezentacja sumy op jest suma macierzy, iloczynu op iloczyn macierzy. Jeżeli istnieje odwrotność operatora to istnieje odwrotność jego macierzy. Reprezentacją op hermitowskiego jest macierz hermiowska.

Operatot jest liniowy gdy dla dowolnych funkcji u oraz stałych α zachodzi: L(α₁u₁+α₂u₂)=α₁Lu₁+α₂Lu₂.

Wspólne wartości własne różnych operatorów: Jeżeli A oraz B komutują ze sobą to mają układ nietrywialnych wspólnych funkcji własnych. Dowód: Niech Ψ_a będzie funkcją własną operatora A, odpowiadającą wartości własnej a: AΨ_a=aΨ_a. Wówczas BAΨ_a=aBΨ_a. Ponieważ A oraz B komutują ze sobą, lewą stronę równania można zapisać w postaci: A(BΨ_a)=a(BΨ_a). Wynika stąd, że B jest również funkcją własna operatora A odpowiadającą wartości własne a. Jeżeli Ψ_a jest liniowo niezależną funkcją własną operatora A, odpowiadającą wartości własnej a, to funkcja BΨ_a może różnić się od Ψ_a co najwyżej o stały mnożnik c,tzn: BΨ_a=cΨ_a(oba wektory mają ten sam kierunek w przestrzen

Hilberta )

Zasada odpowiedniości: (Bohr 1923) 1. Przewidywania teorii kwantowej dotyczące zachowania się dowolnego układu fizycznego muszą w granicy, w której liczby kwantowe określające stan układu stają się bardzo duże, odpowiadać przewidywaniom fizyki klasycznej. 2. Danej regule wyboru podlega cały zbiór wartości odpowiedniej liczby kwantowej. Zatem wszystkie reguły wyboru, które niezbędne sa do otrzymania wymaganej odpowiedniości w granicy klasycznej (duże n) stosują się także w granicy kwantowej (małe n). Operator pędu: Ψ(x,t)=Cos(kx-wt) +iSin(kx-wt). D/dx(Ψ(x,t))=-kSin(a)+ikCos(a)=ik[Cos(a)+iSin(a)];k=p/h, D/dx(Ψ(x,t))=i(p/h)Ψ(x,t), p[Ψ(x,t)]= -ih d/dx(Ψ(x,t)). p=-ihd/dx.( inne: w jaki sposób rozwiązanie dla kwantowego oscylatora harmonicznego spełnia zasadę odpowiedniości? Oblicz klasyczną gęstość prawdopodo. P odpowiadającą jednowymiarowej sprężynie o naturalnej częstości W₀.Przesunięcie i prędkość w chwili t: x=x₀sin(W₀t), v=x₀W₀Cos(W₀t). Pdx jest prawdopodo. Znalezienia cząstki w dowlonym t w przedziale dx wokół x. Jeśli T₀=2Pi/W₀ to Pdx=2dt/T₀=2W₀dt/2Pi, gdzie dt=dx/x' i jest czasem w którym cząstka przebiega odcinek dx w jedną stronę (2 bo dwa razy idzie sobie). dt=dx/W_osqrt(x_o²-x²), Pdx =W₀dt/Pi=dx/Pisqrt(...).Tak znaleziona gęstość jest unormowana w -x_odox_o. Rysunek - wynika ze Kwan.Spe.Zas.Od

Heisenberg: dla p i x: dxdp_x≥h/2Pi (zmienne komplementarne: enrgia i czas, pęd i położenie, L_x i L_y­) Pozwala zrozumieć jak to jest możliwe by promieniowanie i materia miały dwoistą naturę. Nie możemy nigdy jdnocześnie w tym samym doświadczeniu udowodnić, że mają one dwoista naturę; Mechanika układu kwantowego musi być opisywana w języku teorii prawdopodobieństwa, gdyż z zasady nieoznaczoności wynika, że nie jest możliwe z żądaną dokładnością jednoczesne określenie chwilowego pędu i położenia. W rezultacie jesteśmy w stanie przewidzieć jedynie prawdopodobne zachowanie cząstek.

Oscylator harmoniczny...Hamiltonian cząstki o masie m w potencjale V=Kx²/2 jest równy: H=(p²/2)+V, odpowiedn

równanie Sch. ma postać: (-h²/2m) d²/dx²(Ψ)+VΨ=EΨ, w obszarze dozwolonym klasycznieE>V i równanie to możn

zapisać jako: Ψ_xx=-k²Ψ, h²k²(x)/2m=E-Kx²/2>0. Funkcja falowa ma wiec w tym obszarze charakter oscylacyjny. W obszarze klasycznie wzbronionym, gdzie x²>x₀² mamy E<Kx²/2 i otrzymujemy: Ψ_xx=χ²Ψ, h²χ²/2m=(Kx²/2)-E>0 zatem w tym obszarze funkcja falowa nie oscyluje. W obszarze asymptotycznym Kx²>>E i równanie Sch ma postać: Ψ_xx=mKx² Ψ/h²≡α⁴x²Ψ, gdzie α jest charakterysztyczną liczbą falową: α²≡mW₀/h. Wprowadzając bez wymiarowe przesunięcie ξ≡αx, otrzymuję: Ψ_ξξ=ξ²Ψ.Rozwiązanie narastające + nie może spełniać warunku normalizującego: SΨ*Ψdx<inf. i pozostajemy z wykładniczo zanikającą funkcją falową Ψ∼Aexp(-ξ²/2)=Aexp[-(αx)²/2]. Charakter funkcji zmienia się od oscylującego dla x²<x₀²do zanikającego dla x²>x₀², tak że punkty zwrotne x=±x₀ również w mechanice kwantowej mają sens fizyczny.

Moment pędu:J_x=yp_z-zp_y,J_y=zp_x-xp_z,J_z=xp_y-yp_x,[J_x,J_y]=ihJ_z,[J_z,J_x]=ihJ_y,[J_y,J_z]=ihJ_x,[J_z,x,y,J²]=0,J_z,x,yΨ_m=hmΨ_m,

J₊=J_x+iJ_y;J_-=J_x-iJ_y=J₊^t. J_zΨ_m=hmΨ_m, J_zJ₊Ψ_m=(hJ₊+J₊J_z)Ψ_m=(hJ₊+J₊hm)Ψ_m, J_z(J₊Ψ_m)=h(m+1)(J₊Ψ_m); J₊Ψ_m jest nie-

unormowaną funkcją własną operatora J_z, odpowiadającą wartości własnej h(m+1), a więc: J₊Ψ_m=Ψ_m+1, J₊(J₊Ψ_m)= J₊Ψ_m+1=Ψ_m+2, J_-Ψ_m=Ψ_m-1, J_-Ψ_m-1=Ψ_m-2. Ponieważ J² jest przemienne z J_z operatory te mają wspólne funkcje własne. Niech Ψ_m będzie taką wspólną funkcją własną z wartością własną h²K² tj.: J²Ψ_m=h²K²Ψ_m, Dziełając operatorem J₊ otrzymujemy J_­+J²Ψ_m=h²K²(J₊Ψ_m)=J²(J₊Ψ_m),a zatem J₊Ψ_m=Ψ_m+1 jest także funkcją własną operatora J². Wynika stąd, że otrzymane funkcje własne operatora J_z są funkcjami własnymi operatora J², odpowiadającymi tej samej wartości własnej h²K². Ile jest takich funkcji? : <J²>=h²K²=<J_x²>+<J_y²>+<J­­_z²>, h²K²=<J_x²>+<J_y²>+h²m² stąd wynika że: h²K² ≥h²m², |K|≥|m|. Dla danej wartości K>0 możliwe wartości m zawarte są między +K a -K. Jeśli m_max jest największą wartości, jaką może przyjąć m dla danej wartości momentu pędu hK, to: J₊Ψ_mmax=0, J_-Ψ_mmin=0. Dalej J²Ψ_mmax= h²K² Ψ_mmax=J_z²Ψ_mmax+hJ_zΨ_mmax, h²K²=h²m_max(m_max+1), J²Ψ_mmin=h²K²Ψ_mmin=J_z²Ψ_mmin-hJ_zΨ_mmin, h²K²=h²m_min(m_min-1). Stąd wynika, że m_max(m_max+1)=m_min(m_min-1), co jest spełnione gdy m_max=-m_min. Możliwe dla danej wartości J², wartości m układają się w symetryczny ciąg wokół m=0. Przyjmijmy: m_max≡j, ponieważ m przebiega wartości od -j do j, przyjmując kolejno wartości różniące się o jedność, otrzymujemy zatem: j=liczba całkowita, jeśli ciąg wartości m zawiera m=0; j=1/2 liczba nieparzysta jeśli ciąg wartości m nie ma elementu m=0. Ponadto, jeśli m jest liczbą całkowitą, to związane z nią wartości m są liczbami całkowitymi. Jeśli m jest nieparzystą wielokrotnością 1/2 to odpowiadające jej wartości m są także nieparzystymi wielokrotnościami ½. Równania własne: L²Ψ_lm=h²l(l+1)Ψ_lm L_zΨ_ml=hmΨ_m (m=-l...l), L₊Ψ_ml=Ψ_lm+1,L_-=Ψ_ml-1, L₊Ψ_ll=0,L_-Ψ_l,-l=0.

Rachunek zaburzeń nie zdegenerowanych: Hamiltonian: H=H₀+H^', podział hamiltonianu na część H₀, której funkcje własne są znane, oraz dodatkowy wyraz H^', który w pewnym sensie jest mały w porównaniu z H₀. Teoria, która stara się znaleźć przybliżone stany własne całkowitego hamiltonianu H, nosi nazwę rachunku zaburzeń. (H₀ jest nazywany h. nie zaburzonym, natomiast H^' h. zaburzającym. Podstawowym założeniem jest: stany własne i E własne całkowitego H nie odbiegają zbytnio od tych samych H₀. Aby uwidocznić małość zaburzenia H^' wprowadzimy pomocniczy parametr małości α. Równanie ma postać: (H₀+αH^')Ψ_n=E_nΨ_n. Rozwinięcie perturbacyjne: przyjmujemy że stany i E własne H₀ są znane Ponieważ Ψ_n→Ψ_n⁽⁰⁾, gdy α→0 rozwiązanie równania będzie w postaci szereg, w którym Ψ_n⁽⁰⁾ będzie wyrazem wiodącym. Podobnie dla E: Ψ_n=Ψ_n⁽⁰⁾+αΨ_n⁽¹⁾+α²Ψ_n⁽²⁾... E_n=E_n⁽⁰⁾+αE_n⁽¹⁾+α²E_n⁽²⁾...Podst roz do ®ów: [H₀Ψ_n⁽⁰⁾-E_n⁽⁰⁾Ψ_n⁽⁰⁾]+α[H₀Ψ_n⁽¹⁾+H^'Ψ_n⁽⁰⁾-E_n⁽⁰⁾Ψ_n⁽¹⁾ -E_n⁽¹⁾Ψ_n⁽⁰⁾]+α²[H₀Ψ_n⁽²⁾+H^'Ψ_n⁽¹⁾-E_n⁽⁰⁾Ψ_n⁽²⁾-E_n⁽¹⁾Ψ_n⁽¹⁾-E_n⁽²⁾Ψ_n⁽⁰⁾]+...=0

(k... ale równanie). Rozbijamy na układ równań sprzężonych:a) H₀Ψ_n⁽⁰⁾=E_n⁽⁰⁾Ψ_n⁽⁰⁾, b)Ψ_n⁽¹⁾(H₀-E_n⁽⁰⁾)=(E_n⁽¹⁾-H^')Ψ_n⁽⁰⁾ c) Ψ_n⁽²⁾(H₀-E_n⁽⁰⁾)=(E_n⁽¹⁾-H^')Ψ_n⁽¹⁾+E_n⁽²⁾Ψ_n⁽⁰⁾, d) Ψ_n⁽³⁾(H₀-E_n⁽⁰⁾)=(E_n⁽¹⁾-H^')Ψ_n⁽²⁾+E_n⁽²⁾Ψ_n⁽¹⁾+E_n⁽³⁾Ψ_n⁽⁰⁾, Z najniższego przybliżenia widać że Ψ_n⁽⁰⁾ i E_n⁽⁰⁾ są stanami i E własnymi H₀. W równaniu b H₀ działa na Ψ_n⁽¹⁾, co sug że rozw Ψ_n⁽¹⁾ można poszukać w postaci superpozycji stanów własnych H₀. |Ψ_n⁽¹⁾>=∑C_ni |Ψ_i⁽⁰⁾>(13.6), jeżeli to rozwinięcie podstaw do b to otrzymamy:(H₀-E_n⁽⁰⁾)∑C_ni |Ψ_i⁽⁰⁾>=(E_n⁽¹⁾-H^') |Ψ_n⁽⁰⁾>.Pomnożenie lewej strony przez <Ψ_j⁽⁰⁾| daje: (E_j⁽⁰⁾-E_n⁽⁰⁾)C_nj +H^'_jn=E_n⁽¹⁾δ_jn (13.7) gdzie H^'_jn są eleme macierzowy H^' w reprezentacji {Ψ_n⁽⁰⁾}: H^'_jn≡<Ψ_j⁽⁰⁾ |H^' | Ψ_n⁽⁰⁾ >.

Poprawki 1 rzędu: dla j≠n ze wzoru 13.7 dostajemy współczynniki {C_nj}, które podstawione do 13.6 dają poprawkę 1 rzędu do Ψ_n: C_ni=H^'_in/(E_n⁽⁰⁾-E_i⁽⁰⁾), Ψ_n⁽¹⁾=∑H^'_inΨ_i⁽⁰⁾/(E_n⁽⁰⁾-E_i⁽⁰⁾) +C_nnΨ_n⁽⁰⁾. C_nn=0. Dla j=n z 13.7 otrzymujemy popra 1 rzędu do energii E_n. E_n⁽¹⁾=H^'_nn , Są to diagonalne elementy macierzowe operatora H^'. po podstawieniach: Ψ_n=Ψ_n⁽⁰⁾ +∑_i≠n H^'_inΨ_i⁽⁰⁾/(E_n⁽⁰⁾-E_i⁽⁰⁾), E_n=E_n⁽⁰⁾+H^'_nn. Pierwsze mówi nam, że aby rozwinięcie w szereg miało sens współczynniki rozwinięcia powinny być mniejsze od jedności: |H^'_in |<<|E_n⁽⁰⁾-E_i⁽⁰⁾|. Elementy macierzowe operatora H^' winny być małe w porównaniu z różnicą odpowiednich nie zaburzonych energii. Podobnie z 2 rów wynika: |H'_nn|<<|E_n⁽⁰⁾|. Elementy diagonalne hamiltonianu zaburzającego powinny być małe w porów z odpowiednią nie zaburzoną E.

Poprawki 2 rzędu: aby znaleźć poprawkę 2 rzędu do Ψ_n i E_n musimy rozwiązać równanie c) H₀ działa na Ψ_n⁽²⁾, zatem korzystnie jest rozwinąć Ψ_n⁽²⁾ w szereg stanów własnych H₀: Ψ_n⁽²⁾=∑d_niΨ_i⁽⁰⁾, podstawienie do c) daje: ∑E_i⁽⁰⁾d_ni |Ψ_i⁽⁰⁾>+H^'|Ψ_n⁽¹⁾>=E_n⁽⁰⁾∑d_ni|Ψ_i⁽⁰⁾>+E_n⁽¹⁾|Ψ_n⁽¹⁾>+E_n⁽²⁾|Ψ_n⁽⁰⁾>. Pomnożenie lewej strony przez <Ψ_j⁽⁰⁾| prowadzi do: (E_j⁽⁰⁾ -E_n⁽⁰⁾)d_nj+<Ψ_j⁽⁰⁾|H^'|Ψ_n⁽¹⁾>=E_n⁽²⁾δ_jn+E_­n⁽¹⁾<Ψ_j⁽⁰⁾|Ψ_n⁽¹⁾>. Dla j=n z powyższego wynika:E_n⁽²⁾=<Ψ_n⁽⁰⁾|H^'|Ψ_n⁽¹⁾>=∑_i≠n<Ψ_n⁽⁰⁾| H^'H^'_in /(E_n⁽⁰⁾-E_i⁽⁰⁾) | Ψ_i⁽⁰⁾>=∑ H^'_niH^'_in /(E_n⁽⁰⁾-E_i⁽⁰⁾), korzystając z tego że H^' jest operatorem hermitowskim można zapis E_n⁽²⁾=∑_i≠n | H^'_ni|²/(...), po podstawieniach: E_n=E_n⁽⁰⁾+H^'_nn+E_n⁽²⁾. Aby obliczyć porpawki 2 rzędu do Ψ_n musimy znać d_ni dla n≠j dostajemy: (E_n⁽⁰⁾-E_j⁽⁰⁾)d_nj=<Ψ_j⁽⁰⁾|H^' ∑_k≠n H^'_kn /(E_n⁽⁰⁾-E_k⁽⁰⁾)|Ψ_k⁽⁰⁾> - H^'_nn<Ψ_j⁽⁰⁾|∑_k≠nH^'_kn/(E_n⁽⁰⁾-E_k⁽⁰⁾)|Ψ_k⁽⁰⁾> Z drugiej sumy pozostaje jedynie wyraz k=j ze względu na iloczyn skalarny <Ψ_j⁽⁰⁾|Ψ_k⁽⁰⁾>, w pierwszej pozostają wszyst D_nj=1/(E_n⁽⁰⁾-E_j⁽⁰⁾)(∑_k≠n(H^'_jkH^'_kn)/(E_n⁽⁰⁾-E_k⁽⁰⁾))-(H^'_nnH^'_jn)/(E_n⁽⁰⁾-E_j⁽⁰⁾)², d_nn=0, Ψ_n z dokładnością do wyrazów 2 rzędu H^':

Ψ_n=Ψ_n⁽⁰⁾+∑_i≠n[H^'_in/(E_n⁽⁰⁾-E_i⁽⁰⁾)-(H^'_nnH^'_in)/(E_n⁽⁰⁾-E_i⁽⁰⁾)²+∑_k≠n(H^'_ikH^'_kn)/((E_n⁽⁰⁾-E_i⁽⁰⁾)(E_n⁽⁰⁾-E_k⁽⁰⁾))]Ψ_i⁽⁰⁾.

Zdegenerowanych: H=H₀+H^', Ψ_n⁽¹⁾=∑C_niΨ_i⁽⁰⁾, C_ni=H^'_in/(E_n⁽⁰⁾-E_i⁽⁰⁾), jeśli energia jest q-krotnie zdegenerowana to: E₁⁽⁰⁾=E₂⁽⁰⁾=E_q⁽⁰⁾. I C_ni ma nieskończoną wartość dla q≥n,i. Aby tego uniknąć konstruuje się nowy układ funkcji bazowych, takich które diagonalizują podmacierz H^'_in dla q≥n,i. Diagonalizacja: Oznaczmy q funkcji, które diagonalizują H^'_in symbolem Ψ^'_n=∑a_niΨ_i⁽⁰⁾. Te kombinacje liniowe zdegenerowanych stanów własnych z założenia diagonalizują H^'_in, tzn. <Ψ_n^'|H^'|Ψ_p^'>=H^'_npδ_np q≥n,p. Funkcje Ψ_n^' połączone z pozostałym układem stanów nie zdegenerowanych {Ψ_i⁽⁰⁾,i>q} dają bazę: B={Ψ₁^',Ψ₂^',....,Ψ_q^',Ψ⁽⁰⁾_q+1,Ψ⁽⁰⁾_q+2,...}.Na podstawie tej bazy można zbudować macierz H^'. diagonalne elementy podmacierzy H^' o wymiarze qxq są poprawkami 1 rzędu E_n^' do E_n⁽⁰⁾ , q≥n tzn. E_n^'=<Ψ_n^'|H^'|Ψ_n^'>=H_nn^'. Jeśli wszystkie elementy diagonalne są różne to zaburzenie H^' znosi q-krotną degenerację H₀. Dowód powyższej równości: HΨ_n=(H₀+H^')Ψ_n=E_nΨ_n, podstawienie Ψ_n=Ψ_n^' oraz E_n=E_n⁽⁰⁾+E_n^' do równania Schr daje: H^'Ψ_n^'=E_n^'Ψ_n^'. Tutaj skorzystaliśmy z tego że Ψ_n^' będąca liniową kombinacją stanów zdegenerowanych sama także jest stanem zdegenerowanym. Mając zbiór wybrany tak by tworzył on ciąg ortogonalny, można równanie <Ψ_n^'|H^'|Ψ_p^'>=H^'_npδ_np q≥n,p uważać za macierzowy odpowiednik równania operatorowego H^'Ψ_n^'=E_n^'Ψ_n^', jeśli tylko bęzie spełnione: E_n^'=H^'_nn. Skonstruujemy teraz nowe funkcje bazy {Ψ_n^'} które diagonalizują macierz H^'. Są one wyrażone za pomocą współczynników a_ni, które są tak dobrane by {Ψ_n^'} spełniały równanie własne H^'Ψ_n^'=E_n^'Ψ_n^'. H^'∑a_ni|Ψ_i⁽⁰⁾>=E_n^'∑a_ni|Ψ_i⁽⁰⁾>. Pomnożenie z lewej strony przez <Ψ_p⁽⁰⁾| daje : ∑a_niH^'_pi=E_n^'∑a_niδ_pi=E_n^'a_np, ∑(H_pi^'-E_n^'δ_pi)a_ni=0. Dla ustalonego n współczynniki a_ni tworzą jednokolumnową reprezentację Ψ_n^' w bazie Ψ_l⁽⁰⁾, q≥l. Podobnie H_pi^'=<Ψ_p⁽⁰⁾|H^'|Ψ_o⁽⁰⁾> jest przedstawieniem macierzowym H^' w tej samej bazie. Dla każdej wartości n i p wzór ∑(H_pi^'-E_n^'δ_pi)a_ni=0 jest jednym równaniem na E_n^' i na q składowych wektora a_ni. Zmieniając wartość n od 1 do q otrzymamy q układów równań. Warunkiem istnienia nie trywialnego rozwiązania a_ni każdego spośród tych q równań macierzowych jest zerowanie się wyznacznika macierzy współczynników, co prowadzi do równania sekularnego: det|H_pi^'-E_n^'δ_pi|=0, w postaci operatorowej: det|H^'-E_n^'I|=0 Operator jednostkowy ma wymiar qxq. Wartościami własnymi równania H^'Ψ_n^'=E_n^'Ψ_n^' jest q pierwiastków równania det|H_pi^'-E_n^'δ_pi|=0. Podstawienie uzyskanej wartości E do macierzowej postaci równania H^'Ψ_n^'=E_n^'Ψ_n^' pozwala rozwiązać ten układ ze względu na współczynniki a_1i, współczynniki te z kolei dają nową bazę Ψ_n^' w B={Ψ₁^',Ψ₂^', ....,Ψ_q^',Ψ⁽⁰⁾_q+1,Ψ⁽⁰⁾_q+2,...}. Posługując się nową bazą unikamy komplikacji związanych z degeneracją stanów własnych hamiltonianu H₀ i możemy stosować rachunek zaburzeń dla stanów nie zdegenerowanych. (k... wreszcie koniec).

Efekt Starka( a broodwar`a?? ;] ) Z rachunku zaburzeń wynika iż pole elektryczne będzie powodowało częściowe rozszczepienie n²-krotnie zdegenerowanych energii własnych atomów jednoelektronowych. Stark zaobserwował rozszczepienie linii Balmera w polu elektrycznym o natężeniu 100000v/cm . Hamiltonian: H=p_r²/2m + L²/2mr²-eεz =H₀+H^', H^'=-eεz=-eεrcosθ. Stany własne nie zaburzonego hamiltonianu są n²-krotnie zdegenerowane. Zastanówmy się (kocham takie teksty ;]] ) jak zaburzające pole elektryczne rozszczepia te stany. W szczególności rozważmy n=2. W notacji |nlm> funkcje falowe tych stanów są: |200>,|211>,|210>,|21-1>. Aby obliczyć przyrosty energii E₂ musimy rozwiązać równanie sekularne:0=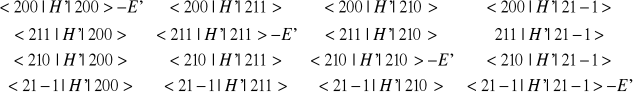

Spośród elementów macierzowych występujących w tym równaniu, tylko dwa są różne od zera. Wszystkie elementy o różnych wartościach liczb m_l są równe zeru ze względu na ortogonalność stanów |nlm_l> W takiej sytuacji mówi się że H^' nie sprzęga stanów o różnych m_l. Całkowanie daje: <210|H^'|200>=<200|H'|210>= -F. Podstawienie tych wartości do wyznacznika( to duże powyżej) daje: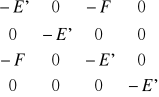
=0 , które ma 4 pierwiastki E'=0,0,F,-F, gdzie F=3|e|εa₀. W ten sposób znaleźliśmy, że z dokładnością do wyrazów najniższego rzędu w polu elektrycznym

ε czterokrotnie zdegenerowany stan n=2 rozszczepia się na trzy stany (od najwyższego do najniższego): E₂ →E₂⁽⁰⁾+F, E₂→E₂⁽⁰⁾, E₂→E₂⁽⁰⁾-F. Aby obliczyć nowe funkcje falowe dla stanu n=2 Ψ=a|200>+b|211>+c|210>+d|21-1> podstawiamy wartości pierwiastków do równania macierzowego: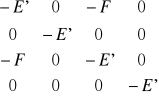
.

=0. Rozwiązaniami są funkcje: E₂⁺=E₂⁽⁰⁾+F→Ψ₊=(1/sqrt(2)) (|200>-|210>), E₂^-=E₂⁽⁰⁾-F→Ψ_-=(1/sqrt(2))(|200>+|210>), E₂⁽⁰⁾=E₂⁽⁰⁾→Ψ=|211> lub Ψ=|21-1>. Zaburzenie miesza stany m=0, podczas gdy stany m=1 i m=-1 pozostaja zdegenerowane. Liczby ±F są średnimi wartościami oddziaływań H' w stanach Ψ_± .

Metoda wariacyjna: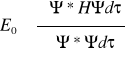
, rozwinięcie dowolnej funkcji w bazie funkcji Ψ_n, Ψ=∑a_nΨ_n, ∑|a_n|²=1, P=∑a_n*Ψ_n*H∑a_nΨ_n=∑a_n*Ψ_n*∑a_nHΨ_n=∑a_n*Ψ­_n*E_nΨ_n=∑|a_n|²E_n>=E₀, dla n=0, L=E₀SΨ*Ψdz=E₀∑a_nΨ_n*a_nΨ_n= E₀∑|a_n|²=E₀. a) stan podstawowy: minimum całki: SΨ*HΨdz=E₀; b) funkcję Ψ przedstawić w funkcji parametrów: SΨ_(α,β,χ)HΨ_(α,β,χ)dz=J_(α,β,χ); c) rozwiązać warunek na minimum: dJ/dα=dJ/dβ=dJ/dχ=..=0, otrzymam wartość parametrów β,α,χ d) znaleźć energię: E=J_(α,β,χ) energia jest równa funkcji wyrażonej przez parametry. Ψ₀=(α,β,χ) jest to funkcja stanu podstawowego. Aby obliczyć kolejne stany dodaję warunek ortogonalności z poprzednimi stanami: E₁=minSΨ₁*HΨ₁dz oraz SΨ₁*Ψ₁dz=1 oraz SΨ₁*Ψ₁dz=0, i tak dalej kolejne stany posiadają o jeden warunek ortonormalności więcej. Przykład: ad a) H=(-h²d²/2mdx² )+uw²x²/2; funkcja przy x→inf Ψ→0; dla funkcji zerowego przybliżenia brak węzłów: Ψ_(x,α)­=Ae^-αxx/2, SΨ*Ψdz=1→A=(α/Pi)^1/4 ad b) J_(α)=SΨ*HΨdz=(1/4)((h²α/2) + (uw²/α)) ad c) dJ/dα=o → α=uw/h, J_(α)=hw/2=E₀ jest to stan podstawowy oscylatora harmonicznego na przykład. Ψ₀=Ψ_(x,α0)=(sqrt(uw/Pih))e^-2uwxx/2h_. Ψ₁(x,β)=Be^-βxx/2, B=sqrt(2β/Pi), J(β)=(3/4)((h²β/u)+(uw²/β)), dJ/dβ=0→E₁=3hw/2 β₀=uw/h, Ψ₁(x,β₀)=(sqrt(2/Pi))(uw/h)^3/4e^-uwxx/2h.

Metoda Hartree`go-F(u)cka ;] Metodę tę najłatwiej uzasadnić posługując się zasadą wariacyjną. Rozważmy układ N fermionów oddziałujących ze sobą siłami dwuciałowymi o potencjale V(r-r') i znajdującymi się w pewnym zewnętrznym potencjale U(r). Równanie Sch: ihd/dt(Ψ(r<sub>1</sub>,g<sub>1</sub>,...,r<sub>n</sub>,g<sub>n</sub>)=HΨ(...), gdzie H=∑((-h<sup>2</sup>/2m)Δ<sub>A</sub>+U(r<sub>A</sub>)) +∑<sub>A<B</sub> V(r<sub>A</sub>-r<sub>B</sub>). Zagadnienie wariacyjne z warunkami ubocznymi rozwiązuje się metodą mnożników Lagrange`a, szukamy zatem stacjonarnych wartości funkcjonału: F({Ψ_A*},{Ψ_A})=<H>-∑_A.B=1α_AB(∑_gSd³rΨ_A*(r,g)Ψ_B(r,g)-δ_AB) z mnożnikami Lagrange'a α_AB. Mnożniki tworzą macierz hermitowską: α_AB=α_AB*. Stwierdzamy dalej że:

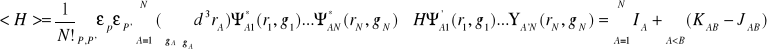
gdzie: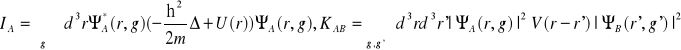

Całka I_A reprezentuje średni jednocząstkowy wkład do energii. Wielkość K_AB opisuje średnią wartość oddziaływania pomiędzy rozkładem ładunku elektronu w stanie Ψ_A i rozkładem ładunku w stanie Ψ_B, jes to tak zwana całka kulombowska. J_AB nosi nazwę całki wymiany. Funkcjonał zależy od zespolonych funkcji Ψ_A. Wariacjom należy poddawać niezależnie część rzeczywistą i urojoną tych funkcji. Równie dobrze wariacji można dokonać względem Ψ_A i Ψ_A^*. Uzyskane w ten sposób równania wariacyjne będą wzajemnie zespolonosprzężone. Wystarczy więc rozważyć tylko te równania które otrzymujemy z wariowania funkcjonału F względem funkcji Ψ_A^*. Obliczamy zatem wariację δ_A^*F przy zmianie δΨ_A^*, ustalając wartości pozostałych jednocząstkowych funkcji falowych. W ten sposób uzyskujemy: δ_A^*F=∑Sd³rδF_A^*(r,g)β_A(r,g), gdzie

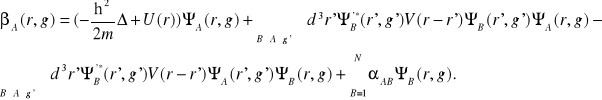
Ponieważ przyrosty δΨ^*_A są dowolne więc rozwiązaniu ekstremalnemu odpowiada β_A(r,g)=0. Uzyskaliśmy zatem N nieliniowych wzajemnie posprzęganych różniczkowo-całkowych równań na N funkcji Ψ_A(r,g). Równania te noszą nazwę równań Hartree-Focka. Drugi człon po prawej stronie powyższego równania opisuje ruch cząstki w średnim potencjale oddziaływania wytworzonym przez wszystkie pozostałe cząstki. Trzeci człon opisuje oddziaływanie nielokalne wynikające z przekrywania się różnych funkcji falowych. Oznaczając średni potencjał symbolem V_AV':

a tzw. Potencjał wymiany symbolem V_­ex

to równania H-F możemy zapisać w postaci:

Wprowadzimy taką unitarną kombinację liniową funkcji Ψ_A, która diagonalizuje hermitowską macierz współczynników Lagrange`a. α_AB=ε gdy A=B, . α_AB=0 gdy A≠B. Dzięki włączeniu wyrazów z A=B potencjały V_AV oraz V_EX nie ulegają zmianie przy unitarnych przekształceniach układu funkcji Ψ_A. Uzyskujemy ostatecznie:

. Jest to układ nieliniowych równań różniczkowo-całkowych typu równania Schrodingera. Mnożąc ostanie równanie przez φ^*_A(r,g), całkując po r i sumując po g można stwierdzić że ε_A jest w przybliżeniu hartree-Focka energią potrzebną do usunięcia cząstki w stanie φ_A z układu (jest energią jonizacji).

---