PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA INSTYTUT POLITECHNICZNY
2004/2005	LABORATORIUM Z METROLOGII
Ćwiczenie nr 4	POMIARY KLINÓW I STOŻKÓW
Budowa i Eksploatacja Maszyn ST. Zaoczne Semestr IV	Dyksik Arnold
Data wykonania		Data	Ocena	Podpis
2005-05-17	T
	S

1. Cel ćwiczenia

Celem ćwiczenia jest zapoznanie się z podstawowymi metodami pomiarów pochyleń klinów i zbieżności stożków, oraz zapoznanie się z zasadami użytkowania, przechowywania i konserwacji przyrządów do pomiarów pochyleń klinów i zbieżności stożków oraz stosowania ich zgodnie z przepisami BHP.

2. Wiadomości teoretyczne

1. Pomiar kąta klina wałeczkami pomiarowymi

Do pomiaru używamy dwóch wałeczków o jednakowej średnicy, płytki wzorcowe i suwmiarki cyfrowej o dokładności pomiaru ± 0,01 mm i płyty pomiarowej. Do pomiaru wielkości B przyjmujemy wielkość stosu płytek wzorcowych H możliwie dużą, aby styk wałeczków z powierzchnią boczną mierzonego stożka występował w pobliżu jego podstawy.

Zasada pomiaru przedstawiona jest na rysunku:

Pochylenie P obliczam z następującego wzoru:

Pochylenie P₁ dla pierwszego pomiaru wynosi:

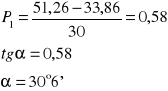
Pochylenie P₂ dla drugiego pomiaru wynosi:

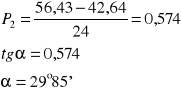
Błąd pomiaru δP określa wzór:

gdzie: δA - błąd pomiaru A

δB - błąd pomiaru B

δh_p - błąd pomiaru stosu płytek wzorcowych

Przyjmuję:

dla błędu pomiaru A - δA = 0,015mm

dla błędu pomiaru B - δB = 0,015mm

dla błędu pomiaru stosu płytek wzorcowych h_p - δh_p = 0,005mm

Zatem błąd pierwszego pomiaru δP wynosi 0,0011mm, a to odpowiada 04'. Kąt klina α = 30^o06' ±0,4'

Dla pomiaru drugiego wyniki są następujące:

Przyjmuję:

dla błędu pomiaru A - δA = 0,015mm

dla błędu pomiaru B - δB = 0,015mm

dla błędu pomiaru stosu płytek wzorcowych h_p - δh_p = 0,005mm

2.2 Pomiar przy użyciu płytek kątowych

Wzorce kątów to: kątowniki 90, wzorce kątów często stosowanych oraz płytki kątowe, zależnie od kształtu powierzchni tworzących kąt prosty rozróżniamy kątowniki powierzchniowe krawędziowe i walcowe. Płytki kątowe odwzorowują wzorce wartości wymiarów kątowych. Są to płaskie wieloboki mające powierzchnie pomiarowe nachylone pod określonym kątami. W użyciu są dwie odmiany wzorcowych płytek kątowych: Johanssona (rys . 1.9.a) i Kusznikowa (rys. 1.9.b).

Sprawdzanie katów za pomocą tych płytek jest bardzo proste i dokładne. Pomiar natomiast jest czasochłonny, gdyż wymaga odpowiedniego kilkukrotnego doboru płytek dla uzyskania dużej dokładności pomiaru. Dokładność kątowa wynosi 12”. Płytki dobiera się tak, aby szczelina świetlna była nie dostrzegalna.

Błąd pomiaru δα określa wzór:

gdzie: δβ - błąd kąta płytki kątowej

s - szerokość szczeliny świetlnej

b - długość przylegania płytki wzorcowej

W przypadku pomiaru szczelina świetlna wyniosła 0, dlatego błąd pomiaru δα = ±24''

Ostateczny wynik pomiaru kąta przy użyciu płytek wzorcowych wynosi 16^o ±24''

1. Pomiar przy użyciu liniału sinusowego

Do pomiaru kąta na sinusnicy potrzebne są :

• Płyta miernicza

• Płytki wzorcowe

• Czujnik z podstawką

• 
  Liniał sinusowy.

Ustawienie klina do pomiaru wykonać zgodnie z rysunkiem.

Wysokość stosu płytek wzorcowych dobieramy tak, aby górna krawędź klina ustawionego na sinusnicy była równoległa do płyty mierniczej. Równoległość tę sprawdzamy czujnikiem. Czujnik przesuwamy w kierunku poprzecznym do klina w jednym a potem w drugim jego końcu. Krawędź klina jest równoległa do płyty mierniczej wtedy, gdy wskazania czujnika w obydwóch końcach są jednakowe. Równoległość realizuje się za pomocą czujnika zegarowego, mierzony kat wierzchołkowy α oblicza się z zależności:

Dla stożków zewnętrznych:

gdzie: L - długość osi wałków liniału sinusowego

h_p - długość stosu płytek wzorcowych

Kąt wierzchołkowy 2α wynosi:

Dla pomiaru pierwszego

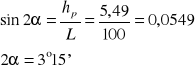
Dla pomiaru drugiego

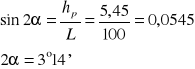
Błąd graniczny pomiaru za pomocą tej metody oblicza się ze wzoru:

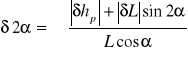
gdzie: δh_p - błąd pomiaru stosu płytek wzorcowych

δL - błąd pomiaru długości liniału sinusowego

Dla pomiaru pierwszego przyjmuję:

δh_p = 0,005mm

δL = 0,05mm

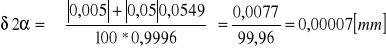
Dla pomiaru drugiego przyjmuję:

δh_p = 0,005mm

δL = 0,05mm

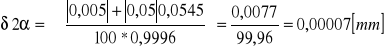
2.4 Pomiar kąta stożka wewnętrznego przy użyciu kulek pomiarowych

Do pomiaru używamy dwóch kulek stalowych o różnych średnicach, głębokościomierza mikrometrycznego i mikrometru.

Mierzymy kolejno długość stożka L, średnicę kulek d₁ i d₂ oraz wymiary A i B.

Wartość kąta α i zbieżność zbieżność można obliczyć ze wzoru:

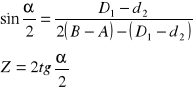
Zaś błąd graniczny pomiaru sinusa połowy kąta α wynosi:

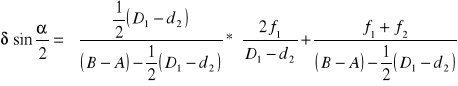
gdzie: f₁ - błąd pomiaru połowy różnicy (D₁-d₂)

f₂ - błąd pomiaru różnicy B-A

Dla pomiaru pierwszego:

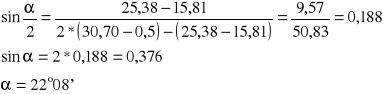
Dla pomiaru drugiego:

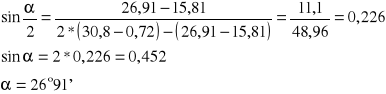
Błąd graniczny dla poszczególnych pomiarów:

Dla pomiaru pierwszego:

Przyjmuję: f₁ = 0,005

f₂ = 0,01

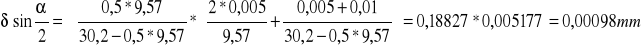
Dla pomiaru drugiego:

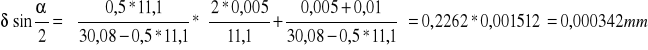
3. Wnioski końcowe

3.1 Ćwiczenie 1 - Pomiar kąta klina wałeczkami pomiarowymi

Na błędy pomiarowe mogą mieć wpływ:

- powierzchnia klina przylegająca do, płyty pomiarowej nie była równa.

- drugi czynnik zależny to siła docisku szczęk suwmiarki i ułożenie ich do elementu mierzonego. Jak widać błąd pomiaru jest niewielki więc ćwiczenie można uznać za wykonane poprawnie.

3.2 Ćwiczenie 2 - Pomiar przy użyciu płytek kątowych

W czasie tego ćwiczenia stwierdziłem, że pomiar jest czasochłonny, gdyż wymaga odpowiedniego kilkukrotnego doboru płytek dla uzyskania dużej dokładności pomiaru.

Można stwierdzić, iż w naszych warunkach laboratoryjnych ćwiczenie zostało wykonane poprawnie.

3.3 Ćwiczenie 3 - Pomiar przy użyciu liniału sinusowego

Podczas tego ćwiczenia stwierdziłem, iż pomiar był utrudniony z powodu, że stożek nie był zamocowany na liniale liniale należało go przytrzymywać podczas pomiaru, drugi czynnik, który utrudniał pomiar to trudność w utrzymaniu końcówki pomiarowej czujnika na maksymalnej średnicy stożka podczas przesuwania statywu z czujnikiem.

3.4 Ćwiczenie 4 - Pomiar kąta stożka wewnętrznego przy użyciu kulek pomiarowych

Z obliczeń błędów pomiarów dla pierwszego i drugiego pomiaru, mogę stwierdzić, iż pomiar drugi został wykonany dokładniej. Trudnością podczas tego pomiaru było mierzenie wielkości B i A z powodu braku odpowiedniego przyrządu do pomiaru od średnicy kulki do górnej powierzchni badanego stożka wewnętrznego.

Przeprowadzenie wszystkich ćwiczeń pomogło mi zapoznać się z budową i własnościami wałeczków pomiarowych, płytek kątowych, liniału sinusowego.

Przy pomiarze kąta płytkami kątowymi, pomiar ten jest czasochłonny, dlatego poleciłbym mierzenie kata kątomierzem, chociaż pomiar płytkami kątowymi jest bardzo dokładny. W czasie ćwiczeń każdy pomiar miał jakieś wady np. podczas pomiaru pierwszego niewielki kłopot sprowadza się do doboru wałeczków pomiarowych i płytek wzorcowych, co zwiększa czas na wykonanie ćwiczenia. Najwięcej kłopotów sprawiał mi pomiar przy użyciu liniału sinusowego ze względu na dobór płytek wzorcowych i ustawienie sinusnicy równolegle do płyty mierniczej.

d_w

1

---