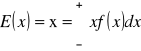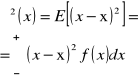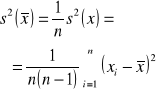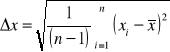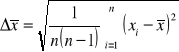2. Rozkład normalny Gaussa

Rozkład Gaussa to rozkład gęstości prawdopodobieństwa z 2 parametrami:

- wartość oczekiwana, średnia,

- wariancja.

Rozkład Gaussa (normalny) opisany jest funkcją gęstości prawdopodobieństwa:

.

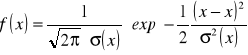
Standardowy rozkład normalny, to taki, którego wartość średnia jest zerowa a wariancja równa 1:

Funkcja gęstości prawdopodobieństwa przyjmuje postać:

.

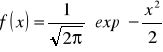
Centralne twierdzenie graniczne

Suma
niezależnych zmiennych losowych, takich że: o wartości średniej
i wariancji
, jest także zmienna losową o wartości średniej
i wariancji
.

3. Wielowymiarowy rozkład normalny. Elipsy kowariancji

Dla ogólnego przypadku n-wymiarowych zmiennych losowych, x i
są wektorami o n elementach każdy. Łączna gęstość prawdopodobieństwa wyrażona jest wzorem:

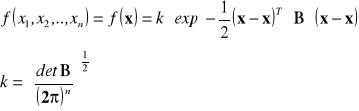
Okazuje się, można to udowodnić, że macierz B jest równa odwrotności macierzy kowariancji C (zdefiniowanej w p. 1.4):

,

Przypomnijmy macierz C::

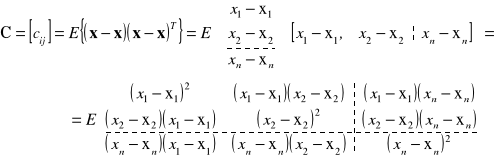
Rozważmy przypadek 2 zmiennych losowych:

Zgodnie z powyższym, macierz kowariancji C ma postać:

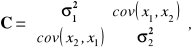
gdzie

a poszukiwana macierz odwrotna
, po odpowiednich przekształceniach, wynosi:

.

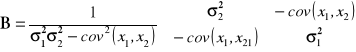
Gdy zmienne losowe są niezależne, i
, wtedy macierz B ma postać:

.

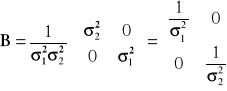
W przypadku 2 zmiennych losowych, rolę przedziału ufności przejmują elipsy kowariancji. Gdy zmiennych jest więcej, mówimy o elipsoidach kowariancji w przestrzeni wielowymiarowej. Pozostańmy przy elipsach kowariancji.

Aby wyznaczyć linie stałej gęstości prawdopodobieństwa, wykładnik exponenty funkcji gęstości prawdopodobieństwa

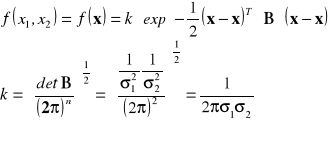
należy przyrównać do wartości stałej, np. do 1:

Obierzmy przykład 2 zmiennych
o wartościach średnich
i o wariancjach
, dla których macierz B wynosi:

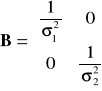
Podstawmy powyższe wielkości do równania na elipsę kowariancji
:

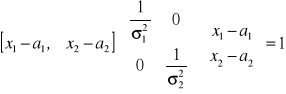
Po wymnożeniu otrzymujemy równanie:

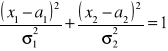
Jest to równanie elipsy na płaszczyźnie
, o osiach
i o środku w punkcie o współrzędnych
. Kąt nachylenia osi elipsy zależy od znaku i wartości współczynnika korelacji
(patrz Rys.3). Trzy przedstawione na Rys. 3 przypadki różnią się wartością i znakiem współczynnika korelacji
.

• ρ=0, zmienne są niezależne, elipsa przechodzi w koło,

• ρ>0, kąt nachylenia osi elipsy 0÷90^o,

• ρ<0, kąt nachylenia osi elipsy 90÷180^o.

Rys.3. Elipsy kowariancji.

Rys. 4. Gęstość prawdopodobieństwa dla dwuwymiarowego rozkładu Gaussa i odpowiadająca mu elipsa kowariancji. Przypadki różnią się tylko wartością współczynnika korelacji
.

Na Rys.4 przedstawione są gęstości prawdopodobieństwa
dla dwuwymiarowego rozkładu Gaussa i odpowiadające im elipsy kowariancji dla współczynnika korelacji: ρ=-0.5, ρ=0.0, ρ=+0.90.

Poziome przekroje tych funkcji są elipsami wzajemnie koncentrycznymi. Dla maksymalnej wartości funkcji elipsa przechodzi w punkt o współrzędnych
: rzut wierzchołka na płaszczyznę
ma współrzędne
.

Pionowe przekroje przechodzące przez wierzchołek to krzywe Gaussa, których szerokości są wyznaczone przez punkty leżące na elipsie kowariancji i są różne dla różnych przekrojów.

Wszystkie inne linie stałego prawdopodobieństwa, gdy wykładnik jest przyrównany do innej stałej c≠1, to także elipsy. Leżą one wewnątrz (gdy c>1) lub na zewnątrz (gdy c<1) elipsy powstałej dla c=1.

Znaczenie elipsy kowariancji dodatkowo ilustruje Rys.5. Punkty leżące na elipsie są jednakowo prawdopodobne co jest określone przez prawdopodobieństwo
. Każdy z punktów leżących wewnątrz elipsy jest bardziej prawdopodobny od punktu leżącego na elipsie, a każdy punkt na elipsie jest bardziej prawdopodobny od punktu leżącego na zewnątrz elipsy. Jest tak niezależnie od tego jakie są geometryczne odległości tych punktów od środka elipsy. Ilustruje to Rys.5.

Rys.5 Względne prawdopodobieństwo dla kilku punktów dla 2-wymiarowego rozkładu normalnego. Punkty na elipsie:
, punkt wewnątrz elipsy:
, punkt na zewnątrz elipsy:

Gdyby x miało nie 2 wymiary lecz n wymiarów, wówczas analogiczne rozumowanie doprowadziłoby do równania:

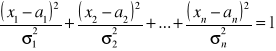
Jest to równanie elipsoidy w przestrzeni n-wymiarowej, to tzw. hiperpowierzchnia. Interpretacja i właściwości są takie same jak w przypadku 2-wymiarowym.

2. Pobieranie próby

Próbą nazywamy skończony zbiór doświadczeń dokonywanych w celu określenia rozkładu badanej zmiennej. Częściej zmierzamy do wyznaczenia parametrów znanego rozkładu, np. wartości średniej i wariancji dla rozkładu normalnego.

Zbiór wszystkich możliwych doświadczeń jest zazwyczaj nieskończony i nazywamy go populacją generalną. Próba n-wymiarowa, to taka, która zawiera n elementów.

Na przykład: W wybranej szkole badamy wzrost uczniów z klas pierwszych. Mamy 6 klas po 30 uczniów. Zatem zbiór wszystkich możliwych przypadków, populacja generalna, to 180 uczniów. W każdej klasie badamy 10 uczniów. Oznacza to, że pobrano próbę 60-wymiarową.

Załóżmy, że pobraliśmy p prób n-wymiarowych dla zmiennej x:

próba 1-sza (ważymy uczniów z klasy nr 1)	(n=10 wyników pomiaru)
.............	.....................
próba i-ta (ważymy uczniów z klasy nr i)	(n=10 wyników pomiaru)
.............	....................
próba p-ta (ważymy uczniów z klasy nr p=6)	(n=10 wyników pomiaru)

Aby pobieranie próby było pobieraniem losowym, łączna gęstość prawdopodobieństwa badanej zmiennej losowej
musi spełniać następujące warunki formalne:

1. poszczególne
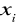
   muszą być niezależne, tzn.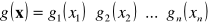
   ,

2. poszczególne rozkłady muszą być jednakowe i identyczne z rozkładem
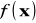
   dla populacji generalnej, tzn.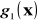
   =...=
   =
   

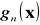
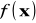
(w klasach są dzieci w równym wieku, żadna klasa nie skupia np. samych przerośniętych repetentów).

Należy podkreślić, że w rzeczywistym pobieraniu próby często dosyć trudno jest zapewnić pełną losowość procesu. O ile 1-szy warunek można zweryfikować porównując poszczególne rozkłady, o tyle warunek 2-gi, odnoszący się do populacji generalnej czasami jest niełatwy do sprawdzenia.

Aby móc posłużyć się wynikami z próby do wyznaczenia parametrów rozkładu, po prostu zakładamy, że próba została pobrana losowo. Nie mamy innej możliwości, należy jednak wiedzieć co to założenie oznacza.

Funkcja zmiennej losowej x, będąca sama zmienną losową, to statystyka. Ważnym przykładem takiej statystyki jest wartość średnia z próby:
. Kolejna n-wymiarowa próba tej zmiennej losowej dostarczy kolejną średnią. W tym sensie wartość średnia z próby jest zmienną losową:

Rozważmy obecnie typowy problem, będący przedmiotem zainteresowania analizy danych: załóżmy, że znamy analityczną postać funkcji, ale nie znamy jednego (lub więcej) parametrów tej funkcji. Parametr ten (parametry) chcemy wyznaczyć na podstawie próby. Mamy tu do czynienia z problemem estymacji parametrów. Estymowane parametry są wyznaczane z próby, są to więc statystyki zwane estymatami, estymatorami (nowa próba, to nowa wartość estymat). Oznaczmy jako
pewien estymator (np. estymator parametru o prawdziwej wartości a wyznaczany jako średnia na podstawie n-wymiarowej próby
).

Estymator S nazywamy nieobciążonym, jeśli
dla każdego n.

Estymator S nazywamy zgodnym, jeśli
.

Estymator nieobciążony i zgodny to taki, którego średnia jest równa wartości rzeczywistej a wariancja jest równa zero.

3. Wartość średnia z próby i wariancja z próby

Pamiętamy, że średnia arytmetyczna z próby (
) to nie jest to samo co wartość oczekiwana (
):

, zachodzi natomiast
.

Oznacza to, że wartość oczekiwana zmiennej losowej (jaką jest średnia z próby) jest równa wartości oczekiwanej tej zmiennej. Inaczej mówiąc: to średnia z wielu średnich staje się bliska wartości oczekiwanej. Nie dotyczy to jednej, dowolnej z takich średnich
.

Uporządkujemy wyrażenia dotyczące średnich, wariancji i dokładności.

Załóżmy, że zmienna losowa x jest mierzona n-krotnie. Czyli: pobieramy próbę o liczebności n z populacji generalnej o gęstości prawdopodobieństwa
odpowiadającej np. rozkładowi normalnemu. Jest to najczęściej spotykana sytuacja pomiarowa.

Dla populacji generalnej		Dla próby n-wymiarowej pobranej z populacji generalnej
Wartość średnia		Wartość średnia
Wariancja z populacji		Wariancja z próby
-	-	Wariancja wartości średniej
-	-	Błąd dowolnego elementu próby
-	-	Błąd wartości średniej

2001-02-09 19

---