1. Wstęp teoretyczny:
Prawo Ohma
Wartości napięcia i natężenia prądu płynącego przez opornik idealny są do siebie proporcjonalne.
Wielkość R jest opornością elektryczną.
I prawo Kirchhoffa
Algebraiczna suma prądów w węźle równa jest zeru.
![]()
II prawo Kirchhoffa
Algebraiczna suma wszystkich napięć wzdłuż dowolnej drogi zamkniętej w obwodzie elektrycznym równa jest zeru.
![]()
Łączenie rezystorów
Szeregowe
Przy połączeniu szeregowym rezystorów, przez każdy rezystor płynie ten sam prąd, natomiast napięcie na połączeniu szeregowym równa się sumie napięć na poszczególnych rezystorach, które są różne i zgodnie z prawem Ohma zależą od wartości rezystancji poszczególnych rezystorów.
Rezystancja zastępcza połączenia szeregowego rezystorów wyraża się wzorem:
![]()
![]()
Rys.1
Równoległe
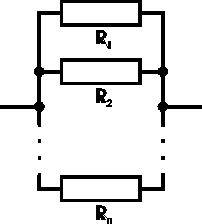
Rys.2
Przy połączeniu równoległym rezystorów, na każdym z rezystorów jest takie samo napięcie, natomiast prąd dopływający do połączenia jest sumą prądów płynących przez poszczególne rezystory, które są różne i zgodnie z prawem Ohma zależą od wartości rezystancji poszczególnych rezystorów.
Rezystancja zastępcza połączenia równoległego rezystorów wyraża się wzorem:
![]()
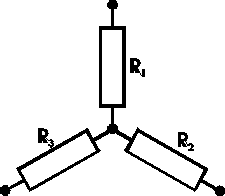
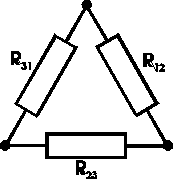
Zamiana gwiazdy na trójkąt i trójkąta na gwiazdę
Rys.3 |
|
Wzory na wartości rezystancji połączeń równoważnych przy zamianie gwiazdy na trójkąt:
![]()
![]()
![]()
..
i trójkąta na gwiazdę:
![]()
![]()
![]()
..
Źródło napięcia
Źródło energii o postaci szeregowego połączenia idealnego źródła napięcia i rezystancji zwanej rezystancją wewnętrzną nazywany rzeczywistym źródłem napięciowym. Idealnym źródłem napięcia nazywamy źródło energii mające rezystancję wewnętrzną równą zeru. Różnica potencjałów biegunów idealnego źródła nazywana jest napięciem źródłowym E.
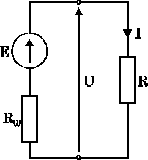
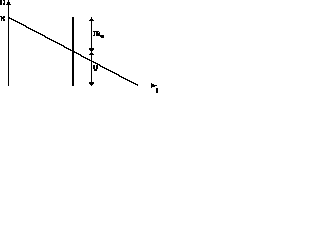
![]()
Rys.5
Rys.4
2. Przebieg ćwiczenia
Prawo Ohma
Należało połączyć układ :
Rys.6
W tym celu należy włączyć amperomierz i woltomierz do układu oraz dowolnie wybrany rezystor z zestawu rezystorów znajdujących się na płycie ćwiczenia. Załączyć napięcie do układu 1, a następnie regulując potencjometrem źródła napięciowego wykonać charakterystykę ![]()
dla wybranego rezystora. Wyniki pomiarów zanotować w tabeli 1.
Tabela 1
|
U |
I |
R |
Lp. |
V |
mA |
Ω |
2,7 |
54 |
50 |
|
5,1 |
102 |
50 |
|
5,8 |
28 |
200 |
|
8,3 |
41,2 |
200 |
U=R·I
U=0,054A·50Ω=27V
U=0,102A·50Ω=5,1V
U=0,028A·200Ω=5,6V
U=0,0412A·200Ω=8,24V
Charakterystyka źródła napięciowego i prądowego
Połączyć układ 2, pozostawiając rozwarte zaciski AB. Załączyć napięcie do układu 2. Regulując potencjometrem źródła napięciowego ustawić napięcie źródłowe E=5V lub E=2V. Zapisać pierwszy punkt w tabeli 2 przy prądzie I równym zero. Ustawić regulowany rezystor R na wartość maksymalną (prawe skrajne położenie), załączyć rezystor na zaciski AB źródła napięciowego. Wykonać serię pomiarów zmniejszając wartość rezystancji od wartości maksymalnej do zera. Wyniki pomiarów zanotować w tabeli 2.
Tabela 2
|
U |
I |
Lp. |
V |
mA |
5 |
0 |
|
4,17 |
20 |
|
3,29 |
40,1 |
|
2,43 |
60 |
|
1,57 |
80 |
|
1,57 |
80 |
|
0,684 |
99,6 |
Prawa Kirchoffa
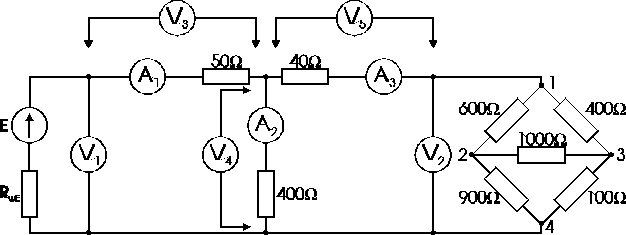
Rys.7
Połączyć układ 4, włączyć mierniki, w miejsca przerwanego obwodu założyć zwory, pozostawiając rozwarte zaciski źródła. Załączyć napięcie do układu 4 i regulując potencjometrem źródła napięciowego ustawić napięcie E=5V. Założyć zwory łączące źródło z resztą obwodu. Sprawdzić czy suma prądów w węźle równa się zero. Wyniki zanotować w tabeli 4.
Tabela 4
I1 |
I2 |
I3 |
∑I |
mA |
mA |
mA |
mA |
16,27 |
8,07 |
8,2 |
0 |
Zgodnie z pierwszym prawem Kirchoffa:
![]()
16,27Ω - 8,07Ω - 8,2Ω= 0
Sprawdzić czy suma napięć w zamkniętych obwodach równa się zero, włączając dodatkowy woltomierz na gałęzie z rezystancjami 50Ω, 40Ω i 400Ω. Wyniki zanotować w tabeli 5.
Tabela 5
|
|
|
|
|
oczko 1 |
oczko 2 |
U1 |
U3 |
U4 |
U5 |
U2 |
∑U |
∑U |
V |
V |
V |
V |
V |
V |
V |
4,29 |
-1 |
-3,29 |
0,33 |
2,96 |
0 |
0 |
![]()
- oczko pierwsze
![]()
- oczko drugie
Zgodnie z drugim prawem Kirchoffa dla pierwszego oczka:
![]()
4,29V - 1V - 3,29V=0
Zgodnie z drugim prawem Kirchoffa dla pierwszego oczka:
![]()
-3,29V + 0,33V + 2,96V = 0
Obliczam ![]()
:
Rys.8
- Wprowadzamy oznaczenia zastępcze rezystorów:
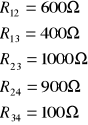
![]()
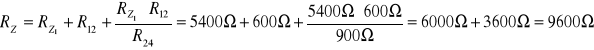
Rezystancja zastępcza całości wynosi ![]()
.
3. Wnioski:
Zgodnie prawem Ohma na podstawie pomiarów a następnie obliczeń, można wywnioskować, że wartości napięcia i natężenia płynącego przez opornik idealny są do siebie proporcjonalne.
Na podstawie drugiego ćwiczenia udowodniliśmy, że algebraiczna suma prądów w węźle równa jest zeru.
Udowodniliśmy prawdziwość Drugiego prawa Kirchoffa, ponieważ algebraiczna suma wszystkich napięć w danym oczku jest równa zero.
Rezystancja zastępcza układu rezystorów w rys.8 wynosi
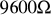
.
Wyszukiwarka
Podobne podstrony:
To będzie nasze nowe sprawko xD, Inżynieria Środowiska PŚk, Semestr 2, Inżynieria Elektryczna
Inżynieria elekryczna, Inżynieria Środowiska PŚk, Semestr 2, Inżynieria Elektryczna
sekuła, inżynieria materiałowa - semestr 4, Inżynieria Materiałowa pwr - semestr 4, Chemia Fizyczna,
BADANIE WYTRZYMAŁOSCI POWIETRZA PRZY NAPIĘCIU PRZEMIENNYM, Politechnika Śląska, Wydział Elektryczny,
elektryczna, Skrypty, UR - materiały ze studiów, IV semestr, inżynieria
elektryczna sciaga, Skrypty, UR - materiały ze studiów, IV semestr, inżynieria
badanie wybranych właściwości oleju, Politechnika Śląska, Wydział Elektryczny, Semestr 3, Inżynieria
IM-opracowane zgadnienia, Politechnika Poznańska, Elektrotechnika, Semestr I, Inżynieria materiałowa
silnik elekrtyczny sprawo, Inżynieria Środowiska PŚk, Semestr 2, Inżynieria Elektryczna
A2-3, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
28fizyczna, inżynieria materiałowa - semestr 4, Inżynieria Materiałowa pwr - semestr 4, Chemia Fizyc
IM 9, Transport Polsl Katowice, 2 semestr, Inżynieria materiałowa, IM
Metoda Brinellatel, Politechnika Lubelska, semestr 1, Inżynieria Materiałowa
sciąga moja, Informatyka SGGW, Semestr 4, Inżynieria oprogramowania, Od starszego rocznika
Tworzenie oprogramowania, Semestr 5, Inżynieria oprogramowania
Wpływ energii mieszania na współczynnik wnikania w układzie ciało stałe - ciecz, pwr biotechnologia(
OPIS DROGI, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynier
Irek, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
więcej podobnych podstron