WPŁYW ENERGII MIESZANIA NA WSPÓŁCZYNNIK WNIKANIA W UKŁADZIE CIAŁO STAŁE-CIECZ
Laboratorium inżynierii chemicznej
SPRAWOZDANIE
1. Wstęp
Rozpuszczanie ciała stałego w mieszalnikach stanowi jedną z prostszych metod realizacji procesu wymiany masy od ciała stałego do cieczy. Szybkość wymiany masy zależy od warunków panujących w bliskim otoczeniu cząstki. W konsekwencji liczba Reynoldsa odnosi się do własności cząstek ciała stałego, a nie mieszalnika czy mieszadła oraz od prędkości poślizgu cieczy względem cząstki. Ruch pojedynczej cząstki ciała w burzliwym strumieniu płynu jest najprostszym przypadkiem burzliwego ruchu mieszaniny dwufazowej .
2. Cel ćwiczenia
Celem ćwiczenia jest wyznaczenie współczynnika wnikania masy od odlewanych walców kwasu salicylowego zawieszonego w kolumnie dyskowej do cieczy poddawanej mieszaniu.
3. Aparatura
kolumna dyskowa
otworki służące do umieszczania ciała stałego wewnątrz kolumny
korki z haczykami na których wiesza się kształtki ciała stałego
zbiornik z którego pompowana jest woda do kolumny
4. Oznaczenia
Dk − średnica kolumny dyskowej
Ds − średnica wewnętrzna statora
D − średnica dysków umieszczona na wspólnym wale
H − wysokość sekcji mieszania
m − masa kształtki kwasu salicylowego
h − wysokość kształtki
dz − średnica zastępcza
dp − średnica podstawy
β − współczynnik wnikania masy od powierzchni ciała stałego do wody
C∗ − stężenie nasycenia kwasu salicylowego w wodzie
C − stężenie w rdzeniu cieczy
![]()
t − czas mieszania
![]()
m − ubytek masy
A − początkowa powierzchnia kształtki
V − objętość wody w instalacji
5. Dane
Dk = 0,2 [m]
Ds = 0,12 [m]
Dm= 0,08[m]
D = 0,8 [m]
H = 0,55 [m]
V = 0,1 [m3]
C∗ =2,2 [kg/ m3] przy 293 K
![]()
t = 45 [min.]
n = 6,66667 obr/s
DAB = 9,08*10 -10![]()
υ = 1,0068* 10 -6 ![]()
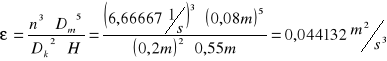
6. Użyte wzory
dz = √[ (dp∗h )+ (dp2 /2)]
β = (![]()
m/ ![]()
t) ∗ (1 / A(C∗- C))
![]()
m = m1 − m2
A = π ∗ (dp/2)2 ∗ h
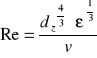
![]()
![]()
7. Przykład obliczeniowy - dla walca numer 1
dz = √ [(33,0∗ 34,4) + (33,02 / 2)] = 40,82 [mm]
A = 3,14 ∗ (33,0/2) 2 ∗ 34,4 = 1782,26 [mm2] = 0,0178226[m2]
![]()
m = 31,560 − 31,490 = 0,070 [g]
β = (0,070/2700) ∗ (1 / 0,0178226 ∗ (2,2 ∗ 103 - 0)) = 6,612*10![]()
[m/s]
![]()
t = 45 ∗ 60 = 2700 [s]
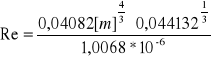
= 4933,313
![]()
= 29,725

8. Dane pomiarowe i wyniki
Na samym początku zważono i zmierzono cztery kształtki kwasu salicylowego (tabela nr 1). Kształtki zawieszono na haczykach i umieszczono w kolumnie, do kolumny wpompowano wodę ze zbiornika obiegowego przez rotametr przy ustalonym natężeniu przepływu 90 dz. , liczba obrotów rotatora została ustalona na 650 obr/min.
Tabela nr 1.
Nr walca |
Masa m1 [g] |
Wysokość walca h1 [mm] |
Średnica walca d1 [mm] |
1 |
31,560 |
34,4 |
33,0 |
2 |
19,946 |
28,4 |
27,9 |
3 |
14,341 |
27,0 |
24,4 |
4 |
4,863 |
17,5 |
17,0 |
Po upływie 45 minut mieszania opróżniono zawartość kolumny, wyjęto kształtki i pozostawiono na kilka dni w celu wysuszenia oraz ponownie je zważono.
Tabela nr 2.
Nr walca |
Masa m2 [g] |
1 |
31,490 |
2 |
19,650 |
3 |
14,132 |
4 |
4,728 |
Opracowane wyniki zestawione zostały w tabeli nr 3.
Tabela nr 3.
Nr. walca |
Δm. [g] |
dz [mm] |
A [m2] |
β [m/s] |
Re |
Sh |
log Re |
log[(Sh-2)/Sc1/3] |
1 |
0,070 |
40,82 |
0,01782 |
6,612∗10-7 |
4933,313 |
29,725 |
3,6931 |
0,4279 |
2 |
0,296 |
34,37 |
0,01735 |
2,872∗10-6 |
3922,359 |
108,71 |
3,0602 |
1,0133 |
3 |
0,209 |
30,93 |
0,01262 |
2,788∗10-6 |
3407,856 |
94,970 |
2,9990 |
0,9534 |
4 |
0,135 |
21,02 |
0,00397 |
5,725∗10-6 |
2036,190 |
132,53 |
2,7755 |
1,1007 |
9.Wykres
10. Wnioski
Wraz ze wzrostem powierzchni geometrycznej danego walca wzrasta wartość współczynnika wnikania masy spowodowane jest to większą powierzchnią kontaktu ciała stałego z cieczą, na duży walec który posiada ostrzejsze krawędzie podstawy, działają dodatkowe zawirowania powodując lepsze rozpuszczanie walca.
- 0 -
Teoretyczne
Wyszukiwarka
Podobne podstrony:
Wyznaczanie współczynnik przepływu w zwężkach pomiarowych dla cieczy, pwr biotechnologia(I stopień),
Wnikanie ciepła w warstwie fluidalnej, pwr biotechnologia(I stopień), IV semestr, Inżynieria chemicz
Wpływ energii mieszania na współczynnik wnikania masy w układzie ciało stałe ciecz
, laboratorium inżynierii chemicznej, sprawozdanie Wpływ energii mieszania na współczynnik wnikania
Wpływ energii mieszania na współczynnik wnikania masy w układzie ciało stałe ciecz
6 Wplyw energii mieszania na w Nieznany (2)
Izotermiczna?sorpcja okresowa w układzie ciało stałe ciecz (2)
Izotermiczna adsorpcja okresowa w układzie ciało stałe - ciecz, inżynieria chemiczna lab, sprawka, 2
Izomeryczna adsorpcja okresowa w układzie ciało stałe - ciecz 2, Dokumenty(1)
IZOTERMICZNA ADSORPCJA OKRESOWA W UKŁADZIE CIAŁO STAŁE - CIECZ 3, Dokumenty(1)
Wpływ sposobu mieszania na zmiany fizyczne rozdrobnionego mięsa ryb
Rdzany, Zbigniew Wpływ energii geotermalnej na dynamikę strumieni lodowych lądolody warty w Polsce
ćw. 8 - Adsorpcja na granicy faz ciało stałe-ciecz, Chemia fizyczna
Sprawko+ +Adsorpcja+na+granicy+faz+ciało+stałe ciecz +Wyznaczanie+adsorpcji+barwnika+na+węglu+aktywn
Absorbcja na granicy?z ciało stałe – ciecz
19 ADSORBCJA NA GRANICY FAZ CIAŁO STAŁE CIECZ WYZNACZANIE ADSORBCJI BARWNIKA NA WĘGLU AKTYWNYM
więcej podobnych podstron