1. Klasyfikacja obciążeń. Prawo Hooke'a. Wykresy rozciągania i ściskania. Naprężenia dopuszczalne.
Klasyfikacja obciążeń
- rozciąganie - 2 siły przeciwnie skierowane działające wzdłuż tej samej osi (osi symetrii przekroju)
- ściskanie - 2 siły przeciwnie skierowane działające wzdłuż tej samej osi (osi symetrii przekroju)
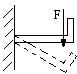
- zginanie - siła działa prostopadle do ciała (belki); belka (element zginany)
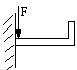
- skręcanie - w płaszczyznach prostopadłych do osi działającej pary sił
Prawo Hooke'a - przyrost długości pręta rozciąganego, w pewnym obszarze obciążeń, jest proporcjonalny do wzrostu siły rozciągającej i długości pręta, a odwrotnie proporcjonalny do pola przekroju poprzecznego i stałej materiałowej.
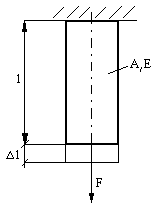
F - siła rozciągająca
l - długość próbki [mm]
∆l - przyrost długości [mm]
A - pole powierzchni przekroju poprzecznego [mm2]
E - moduł Younga, stała materiałowa [MPa]
![]()
б![]()
- naprężenia przy rozciąganiu
![]()
- odkształcenie względne
Ε=б/E - prawo Hooker'a
Wykresy rozciągania - Próby rozciągania wykonuje się na maszynach wytrzymałościowych zwanych zrywarkami. W próbach tych stosuje się próbki o różnych przekrojach i kształtach w zależności od rodzaju materiału, z którego są te próbki wykonane. Najczęściej stosuje się próbki o przekroju kołowym.
Dla stali niskowęglowej
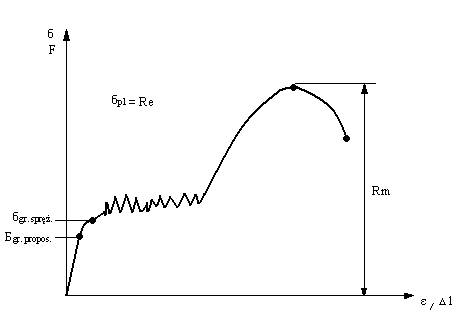
![]()
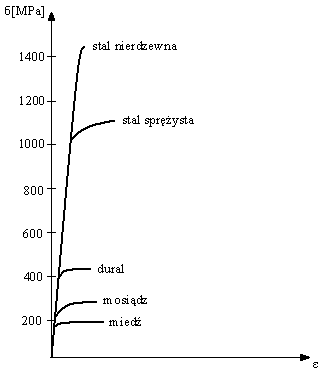
Dla innych materiałów
Wykres ściskania
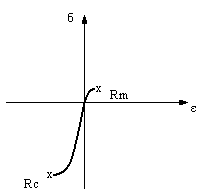
Naprężenia dopuszczalne
бr![]()
- warunek wytrzymałościowy przy rozciąganiu
![]()
![]()
- współczynnik bezpieczeństwa odniesiony do granicy wytrzymałości
![]()
![]()
- współczynnik bezpieczeństwa odniesiony do granicy plastyczności
kc - naprężenia dopuszczalne przy ściskaniu
ks - naprężenia dopuszczalne przy skręcaniu
kt - naprężenia dopuszczalne przy ścinaniu
kg - naprężenia dopuszczalne przy zginaniu
kd - naprężenia dopuszczalne przy dociskaniu
2. Ścinanie. Liczba Poissona. Związek między modułami E,G i ν
Ścinanie
б - τ
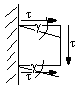
γ - kąt odkształcenia postaciowego
![]()
ε=б/E
G - moduł sprężystości postaciowego (stała materiałowa)
![]()
Liczba Poissona
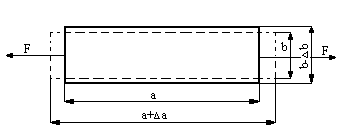
![]()
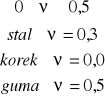
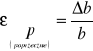
![]()
![]()
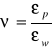
3. Pojęcie siły tnącej i momentu zginającego. Zalezności między T i Mg
Siła tnąca - w rozpatrywaniu przekroju belki jest to siła wewnętrzna prostopadła do osi belki równa sumie rzutów wszystkich sił działających po jednej stronie rozpatrywanego przekroju na oś prostopadłą do osi belki.
Moment gnący(zginający) - siła wewnętrzna równa sumie momentów wszystkich sił działających po jednej stronie rozpatrywanego przekroju względem osi prostopadłej do płaszczyzny zginania przechodzącej przez środek ciężkości rozpatrywanego przekroju.
Zalezności między T i Mg
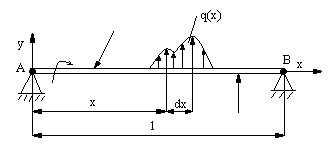
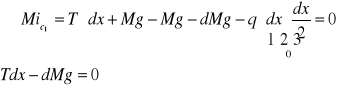
![]()
Siła tnąca w rozpatrywanym przekroju jest równa pochodnej momentu tnącego względem długości.
![]()
![]()
Obciążenie ciągłe równa się pochodnej siły tnącej względem długości
4. Momenty bezwładności figur płaskich
Momentem bezwładności figury płaskiej względem osi nazywamy sumę iloczynów elementarnych pól tej figury i kwadratów odległości tych pól od osi.
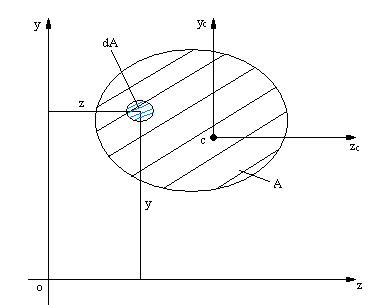
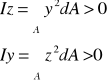
Momenty bezwładności podstawowych figur
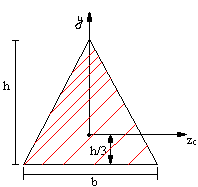
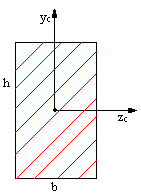
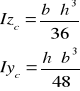
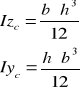
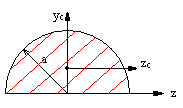
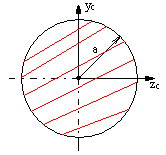
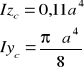
![]()
Tw. Steinera - każdą oś figury płaskiej, która przechodzi przez środek ciężkości nazywa się osią centralną, a moment bezwładności względem tej osi nazywa się centralnym momentem bezwładności.
5. Naprężenia przy zginaniu. Warunek wytrzymałościowy.
бgy![]()
бgmax![]()
бgmax![]()
- warunek wytrzymałościowy przy zginaniu
6. Wskaźnik przekroju
![]()
- wskaźnik przekroju (wskaźnik wytrzymałości przy zginaniu)
7. Linia ugięcia belek.
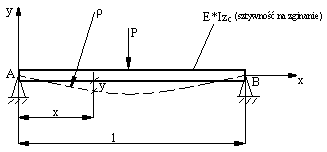
![]()
![]()
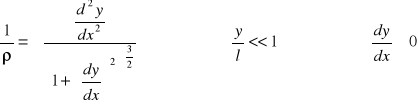
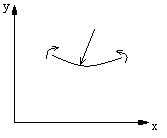
Mg>0 ![]()
Wartości strzałek i kątów ugięcia obliczone zostały w oparciu o równanie różniczkowe linii ugięcia
EJy”=Mg
8. Skręcanie wałów o przekroju kołowym. Obliczanie naprężeń oraz odkształceń wałów. Warunek wytrzymałościowy.
Skręcanie wałów o przekroju kołowym
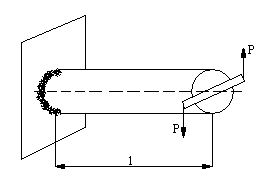
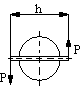
Ms=P*h
![]()
φ - kąt skręcenia
Naprężenia przy skręcaniu. Warunek wytrzymałościowy
- przy skręcaniu powstają naprężenia styczne
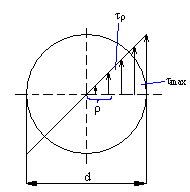
![]()
Io - biegunowy moment bezwładności
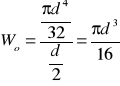
![]()
![]()
![]()
![]()
9. Przeliczanie mocy i liczby obrotów na moment skręcający
Zależność pomiędzy momentem skręcającym (Ms), masą (N) i obrotami (n)
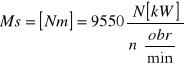
10. Wytrzymałość złożona. Hipotezy wytrzymałościowe. Pojęcia naprężenia zredukowanego.
Wytrzymałość złożona (elementy o przekroju kołowym)
- rozciąganie
- zginanie
- skręcanie
Jednoczesne występowanie tych prostych przypadków obciążenia nazywamy wytrzymałością złożona.
Hipotezy wytrzymałościowe
1. Określono wiele hipotez wytrzymałościowych w zależności od rodzaju materiału. Dwie najpopularniejsze, najczęściej stosowane to:
a) hipoteza maksymalnych naprężeń stycznych (τmax); mówi ona ,że o zniszczeniu materiału decydują największe naprężenia tnące (styczne).
b) hipoteza H.M.H.(Huber-Misesa-Henckye'go); mówi ona o tym, że o zniszczeniu materiału decyduje energia odkształcenia postaciowego.
2. Przypadku naprężeń normalnych i stycznych (zginanie + skręcanie) to wyrażenia na naprężenia zredukowane dla wymienionych hipotez maja postać:
a) dla hipotezy τmax :
![]()
b) w przypadku hipotezy Hubera:
![]()
Naprężenia zredukowane - to takie umowne naprężenia otrzymane po zastosowaniu przyjętej hipotezy wytrzymałościowej (wytężeniowej) dla danego trójkierunkowego (złożonego) stanu naprężeń, które jest równoważne z naprężeniem przy zwykłym (jednokierunkowym) rozciąganiu.
11. Metoda elementów skończonych (MES) Finie Element Metod
MES jest to obecnie jedna z najczęściej stosowanych metod rozwiązywania różnych problemów inżynierskich. Jej uniwersalność polega na łatwości schematyzacji różnych obszarów o skomplikowanej geometrii, także niejednorodnych. MES w najprostszej wersji służy do analizy statyki dowolnych układów mechanicznych. Przez analizę rozumie się wyznaczenie sił wewnętrznych i zewnętrznych oraz odkształceń i przemieszczeń. Duże ciało/belkę dzielimy na setki, tysiące skończonych elementów. W punktach styku (węzłach) piszemy statyczne równania.
Rozwiązanie problemów za pomocą MES:
1.Zbudowanie modelu obliczeniowego 2.Analiza poszczególnych elementów
3.Analiza zbioru elementów układu obliczeniowego
4.Ustalenie warunków brzegowych 5.Rozwiązanie globalnego układu równań
6.Obliczenie wymaganych wielkości na poziomie pkt. 7.Prezentacja wyników
.
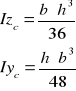
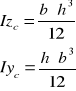
![]()
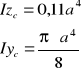
![]()
![]()
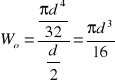
![]()
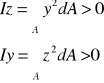
Wyszukiwarka
Podobne podstrony:
Materiałoznawstwo II, pwr, Materiałoznawstwo
Struktury Rynkowe - Pytania - Kolokwium II, PWR, Struktury Rynkowe+
plan skp II, pwr, skp
certyfikat Arka wersja II, PWr - W2, 6 sem, Fizyka budowli
QUAD II pwr Schematic Diagram
obwody ciae ga, Materiały PWR elektryczny, Semestr 2, semestr II, TEORIA OBWODOW 1
Egzamin z Wytrzymałości Materiałów II - Zagadnienia 2012, PWr Mechaniczny [MBM], Semestr 4, Wytrzyma
Wytrzymałość, PWr - ZIP, Wytrzymałość materiałów II, Wykład dr Dzidowski, Opracowanie egzamin, Różne
materialukurwy, PWR ENERGETYKA sem II, Materiałoznawstwo
materiały II koło, pwr, Materiałoznawstwo
PROGRAMOWANIE KONiec, Materiały PWR elektryczny, Semestr 2, semestr II, PROGRAMOWANIE, zad na kolo
S, Materiały PWR elektryczny, Semestr 2, semestr II, PROGRAMOWANIE
Projekt-z-hartowania-stali-1, MBM PWr W10, II stopień, projektowanie materiałów inżynierskich
Człon inercyjny II rzędu, PWr W9 Energetyka stopień inż, III Semestr, Podstawy automatyki, PODSTAWY
ROZC~1, PWr - ZIP, Wytrzymałość materiałów II, Laboratorium
niezerowe, Materiały PWR elektryczny, Semestr 2, semestr II, PROGRAMOWANIE, zad na kolo
Fizyka II, Materiały PWR elektryczny, semestr 3, FIZYKA 2, fizyka do egzaminu, Fizyykaa
więcej podobnych podstron