Akademia Górniczo-Hutnicza

im. Stanisława Staszica

Sprawozdanie

TENSOMETRIA

22.05.2004

Wojciechowska Karolina

Wrona Filip

Rok: II B Grupa: 12b

Wydział Inżynierii Mechanicznej

i Robotyki

Rok akademicki 2008/2009

Ćwiczenie T4

1.1. Temat.

Wyznaczenie wartości i kierunków naprężeń głównych.

1.2. Opis Ćwiczenia.

Podczas wykonywania ćwiczenia zapoznaliśmy się z tensometryczną metodą wyznaczania położenia kierunków naprężeń głównych oraz ich wartości dokonując pomiarów odkształceń za pomocą tensometrów naprężno - oporowych.

1.3. Schemat układu pomiarowego.

Na tarczy została naklejona rozeta prostokątna. Tarcza była umocowana w szczękach tak jak pokazuje rysunek poniżej i była ściskana siłą 20kN. Pomiary dokonywane były mostkiem TSA-4.

1.4. Dane i wyniki pomiaru.

Kierunek ϕ - 0^o		Kierunek β - 45^o		Kierunek γ - 90^o
M0	MP	M0	MP	M0	MP
14,7	14,81	14,59	14,53	14,7	14,59

P = 20 000 N - siła ściskająca;

E = 2,1 * 10⁵ MPa - moduł Younga;

υ = 0,3 - Liczba Poissona;

k = 2,0 - współczynnik czułości tensometru;

k_rz = 1,95 - współczynnik czułości tensometru;

ε₀ - wydłużenie jednostkowe na kierunku ϕ;

ε₄₅ - wydłużenie jednostkowe na kierunku β;

ε₉₀ - wydłużenie jednostkowe na kierunku γ;

1.5. Podstawowe zależności do wykonania obliczeń.

1.6. Obliczenia.

Obliczam wydłużenia na kolejnych kierunkach:

Obliczam wartość naprężeń głównych maksymalnych i minimalnych.

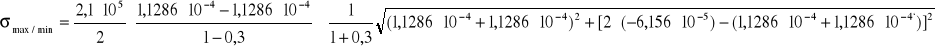
Obliczam wartość maksymalnych naprężeń stycznych.

Obliczam kąt między kierunkiem działania maksymalnych naprężeń a czujnikiem tensometrycznym rozety prostokątnej o położeniu 0^o.

Obliczam naprężenia na kierunkach dowolnych korzystam ze wzorów (na kierunkach obróconych o kąt α względem kierunku działania maksymalnych naprężeń):

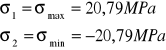
Obliczam naprężenia na kierunku x (kierunek ϕ rozety tensometrycznej prostokątnej):

1.7. Wnioski.

Przez zastosowanie tensometrycznej techniki pomiarowej w zakresie pomiarów czujnikami naprężno - oporowymi, mogliśmy w prosty sposób określić wartość oraz kierunek naprężeń powstałych w ściskanej osiowo stalowej tarczy. Był na niej naklejony czujnik tensometryczny. Pomiaru dokonywaliśmy metodą mostka zerowego przy użyciu mostka TSA-4.

1.8. Koło Mohra dla naprężeń na kierunkach 1,2 i x,y.

σ_x=18,25; σ_y=18,25;

σ₁= 20,79 σ₂=20,79;

τ_xy=9,95

Ćwiczenie T3

2.1. Temat.

Transformacja stanu naprężenia do odpowiadającego stanu składowych sił wewnętrznych.

2.2. Opis Ćwiczenia.

Podczas tego ćwiczenia zapoznaliśmy się z praktycznym sposobem pomiaru naprężeń i obliczania sił wewnętrznych w kratownicy płaskiej przez pomiary tensometryczne. Do tego celu użyliśmy wzmacniacza tensometrycznego HDV2555 podłączonego do komputera.

2.3. Schemat konstrukcji.

Kratownicę płaską wykonano z prętów kątownikowych L25x25x3 i zamocowano w węzłach za pomocą śrub M8.

Kratownicę poddaliśmy rozciąganiu siłą P=7kN.

2.4. Przekrój prętów kratownicy.

2.4. Schemat obliczeniowy.

Rys. Schemat obliczeniowy N.N Aistowa dla obliczeniowej transformacji stanu naprężenia do odpowiadającego składowych sił wewnętrznych.

Przekrój obciążony jest dwoma składowymi momentami zginającymi M_X, M_Y, oraz siłą N.

2.5. Zależności.

Wzory określające wartości naprężeń w funkcji siły osiowej i składowych momentów gnących:

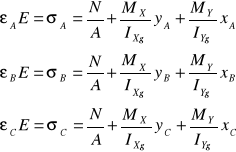
gdzie:

ε_A­­­­­, ε_B­,­­­­ ε_C - wartości odpowiednich odkształceń w badanych punktach A, B, C­­­­;

σ_A, σ_B, σ_C - wartości odpowiednich naprężeń w badanych punktach A, B, C­­­­;

I_xg, I_yg­ - główne centralne momenty bezwładności przekroju;

A - pole przekroju poprzecznego kątownika;

E - moduł Younga dla materiały kątownika;

x_A,x_B,x_C, y_A,y_B,y _C - współrzędne punktów naklejenia tensometrów naprężno - oporowych ;

Rozwiązując powyższy układ równań względem sił wewnętrznych otrzymamy równania N.N. Aistowa od nazwiska ich autora:

Pole przekroju badanego kształtownika: A=1,45 cm²

Momenty bezwładności przekroju kątownika: I_X =1.3 cm⁴, I_Y=0.33 cm⁴

Współrzędne naklejenia tensometrów w odniesieniu do głównych centralnych osi bezwładności przekroju wynoszą:

x_A=5,94mm; x_B=-9,81mm; x_C=5,94mm;x_D=-9,81mm;

y_A=16,26mm; y_B=-1,41mm; y_C=16,261mm;y_D=1,41mm;

Wartość momentów bezwładności w przekrojach I i II oblicza się z zależności (składanie geometryczne wektorów momentów):

2.6. Wyniki pomiarów.

L.p.	x [mm]	y [mm]	N [kG]	N [N]	MX [kGm]	MX [Nm]	MY [kGm]	MY [Nm]	MgWYP [Nm]	σ [Pa]
Przekrój I
1	0,310	1,340	430,81	4226,25	-486,53	-4772,86	-131,65	-1291,49	4944,506	-323,9
2	-0,610	-0,420	332,42	3261,04	-366,79	-3598,21	-189,80	-1861,94	4051,412	701,8
3	0,310	-1,340	468,09	4591,96	-486,53	-4772,86	-189,40	-1858,01	5121,757	679,1
4	-0,610	0,420	566,48	5557,17	-366,79	-3598,21	-101,25	-993,26	3732,785	464,8
	Wartość średnia:		449,45	4409,10	-426,66	-4185,53	-145,52	-1427,55	4422,28
Przekrój II
5	0,310	1,340	410,17	4023,77	-484,78	-4755,69	-159,18	-1561,56	5005,502	-362,4
6	-0,610	-0,420	290,33	2848,14	-338,93	-3324,90	-230,01	-2256,40	4018,246	737,7
7	0,310	-1,340	455,58	4469,24	-484,78	-4755,69	-192,99	-1893,23	5118,682	637,0
8	-0,610	0,420	575,43	5644,97	-338,93	-3324,90	-122,16	-1198,39	3534,275	518,7
	Wartość średnia:		432,88	4246,55	-411,86	-4040,35	-176,08	-1727,34	4394,102

Wartości N, M_y, M_x zostały obliczone przez oprogramowanie komputerowe i przedstawione na wydruku.

2.7. Zestawienie wyników.

Punkt pomiaru	N [N]	MX śr [Nm]	MY śr [Nm]	Mg WYP [Nm]
I	4409,10	-4185,53	-1427,55	4422,28
II	4246,55	-4040,35	-1727,34	4394,102

2.8. Wykres momentów działających na kratownicę.

2.9. Wykresy naprężeń kątowników.

Przekrój I Przekrój II

2.10. Wnioski.

Według definicji w kratownicy węzły stanowią bez tarciowe przeguby, a w prętach kratownicy powstają jedynie siły rozciągające lub ściskające, wywołujące naprężenia normalne o równomiernym rozkładzie na długości pręta. W rzeczywistości jednak kratownica ulega odkształceniom w wyniku których węzły ulegają przemieszczeniu i obrotowi. W prętach kratownicy powstają momenty gnące i siły poprzeczne oprócz sił osiowych. Rzeczywisty charakter pracy ustroju kratowego jest zbliżony do ustroju bramowego, w którym istotny wpływ na przemieszczenie węzłów mają wewnętrzne siły osiowe. Gdyby ustrój pracował jak w idealizowanym modelu obliczeniowym, na całych długościach prętów mielibyśmy do czynienia jedynie z rozciągającą siłą osiową, zaś z wykresów powyżej wynika, że występują momenty zginające, czyli mamy do czynienia ze ściskanie lub rozciąganiem mimośrodowym, przykład - jak na rysunku poniżej:

Zastosowanie tensometrycznych technik pomiaru pozwala na wyznaczenie rzeczywistego stanu naprężenia jaki panuje w obciążonej kratownicy. Sam pomiar, przy użyciu tensometrów naprężno - oporowych nie sprawia żadnych trudności, jest szybki do wykonania, jest dokładnym pomiarem. Na pewno jednak wcześniejsze przygotowanie kratownicy, tzn. dobór tensometrów, naklejenie ich i zabezpieczenie, czy przygotowanie oprogramowania zajęło wykonującym dużo czasu i wymagało dobrej znajomości zagadnienia pomiarów tensometrycznych.

3. Literatura.

1. „Wytrzymałość materiałów - część IV: Eksperyment w wytrzymałości materiałów” - red. Stanisław Wolny; Kraków 2002;

2. „Ćwiczenia laboratoryjne z wytrzymałości materiałów” - A. Siemieniec, A Skorupa; AGH, Kraków 1994;

12

---