2 PDF

WYTRZYMAŁOŚĆ MATERIAŁÓW

1. PODSTAWOWE POJĘCIA WYTRZYMAŁOŚCI MATERIAŁÓW

1) Przedmiot wytrzymałości materiałów, charakterystyka przedmiotu

Wytrzymałość materiałów jest nauką stosowaną, zajmującą się badaniem praw i zjawisk fizycznych, jakim podlegają ciała stałe odkształcalne. Przedmiot wytrzymałości materiałów obejmuje badania teoretyczne i doświadczalne procesów odkształceń i niszczenia ciał pod wpływem różnorodnych oddziaływań (obciążeń).

Zadanie wytrzymałości materiałów polega na dostarczeniu podstaw teoretycznych do wybrania odpowiedniego niego materiału i takiego ukształtowania obiektu, aby w warunkach pracy nie uległ on zniszczeniu bądź przez utratę spójności materiału, bądź przez takie zmiany kształtu, które uniemożliwią jego użytkowanie. Sprowadza się to do określenia rodzaju i wielkości bezpiecznych obciążeń oraz rodzaju i wielkości bezpiecznych odkształceń poprzez spełnienie następujących warunków:

- warunek wytrzymałościowy: w obszarze całego analizowanego elementu przewidziane dla niego obciążenia nie mogą powodować utraty spójności materiału, czyli przekroczyć wartości dopuszczalnej ((obciążenie/charakterystyka geometryczna <=wielkość dopuszczalna))

- warunek sztywnościowy: odkształcenia elementu nie mogą przekraczać wartości uniemożliwiających jego normalną eksploatację ((przemieszczenie < wielkość dopuszczalna))

- warunek stateczności: spełnienie go ma zapobiec nagłym zmianom kształtu lub położenia danego elementu

W wytrzymałości materiałów wykorzystuje się wyniki badań doświadczalnych, które określają właściwości fizyczne materiałów oraz relacje pomiędzy obciążeniami i odkształceniami.

2) Modele obliczeniowe stosowane w wytrzymałości materiałów

Jedną z cech przedmiotu wytrzymałości materiałów jest korzystanie z metod przybliżonych i założeń upraszczających. Stosowane założenia i uproszczenia dotyczące opisu materiałów oraz kształtu rozważanych obiektów i działających na nie obciążeń prowadzą do pojęcia modelu, czyli pewnej idealizacji.

1. modele materiałów: przyjmuje się, że materia wypełnia obiekt w sposób ciągły. Jeżeli można przyjąć, że w każdym punkcie ciała właściwości materiału są jednakowe, to materiał taki nazywamy jednorodnym. Właściwości fizyczne mogą być różne w różnych kierunkach. Materiał taki nazywamy anizotropowym. Jeżeli właściwości materiału są jednakowe we wszystkich kierunkach, to materiał nazywamy izotropowym. Odkształcenia obiektów mogą mieć charakter sprężysty (odwracalny) lub plastyczny (nieodwracalny). Ciała rzeczywiste odkształcają się zarówno sprężyście, jak i plastycznie, przy czym w pewnych sytuacjach występuje przewaga jednych właściwości nad drugimi. Mówimy wówczas o modelu ciała idealnie sprężystego lub idealnie plastycznego. Zastosowanie danego rodzaju modelu zależy od budowy wewnętrznej materiału rzeczywistego, wielkości obciążenia, temperatury, itp.

2. modele elementów konstrukcji: podstawowym kryterium podziału elementów konstrukcji dla potrzeb wytrzymałości materiałów jest ich kształt i sposób pracy. Rozróżnia się następujące rodzaje modeli:

- pręty: jeden z wymiarów (długość) jest wielokrotnie większy od dwóch pozostałych. Oś pręta może być prosta lub krzywoliniowa. Mogą one pracować jako pojedyncze elementy bądź w grupach (kratownice, ramy, itp.)

- ustroje powierzchniowe (cienkościenne): posiadają jeden z wymiarów (grubość) wielokrotnie mniejszy od pozostałych. Należą do nich tarcze (obciążone w swojej płaszczyźnie), płyty (obciążone prostopadle do ich płaszczyzny) i powłoki (obciążone dowolnie) o jedno- lub dwukrzywiznowej powierzchni środkowej.

- ustroje bryłowe: posiadają wszystkie trzy wymiary jednakowego rzędu.

3) Klasyfikacja obciążeń

Podstawową grupę obciążeń obiektów rozpatrywanych w wytrzymałości materiałów stanowią siły będące wyrazem wzajemnego mechanicznego oddziaływania ciał na siebie. Oprócz tego obiekty mogą być poddane obciążeniom cieplnym, elektromagnetycznym, radiacyjnym i innym. Siły zewnętrzne (obciążające) dzielone są na powierzchniowe i objętościowe. Siły zewnętrzne powierzchniowe przyłożone są w do powierzchni ciała i mogą mieć charakter skupiony bądź rozłożony. Siły objętościowe są to siły działające w zewnętrznych obszarach i wynikające z jego masy (siła ciężkości, siły bezwładności). Według innego kryterium wyróżniamy siły czynne i bierne (reakcje więzów).

4) Siły wewnętrzne przekrojowe.

Siły wewnętrzne są wynikiem wzajemnych oddziaływań poszczególnych cząstek materiału należących do tego samego ciala odkształcalnego, wywołanych zrównoważonym obciążeniem zewnętrznym. Oddziaływania te określa się metodą myślowych przecięć.

Rozpatrujemy ciało o dowolnym kształcie, podparte w sposób zapewniający mu równowagę statyczną:

Pw - wektor główny

Mcw - moment ogólny

T - siła tnąca

N - siła normalna

Mg - moment gnący

Ms - moment skręcający

Dokonujemy myślowego przecięcia rozpatrywanego ciała dowolną płaszczyzną i myślowo odrzucamy część (1). W celu utrzymania w równowadze części (2) należy przyłożyć do niej na powierzchni rozpatrywanego przekroju układ sił wewnętrznych, jakimi działają na nią cząstki usuniętej części (1). Pomijając chwilowo zagadnienie rozkładu sił wewnętrznych w przekroju, możemy określić wektor główny Pw oraz moment ogólny Mcw tych sił.

Jeżeli w ustroju prętowym wystąpi tylko jedna składowa tych sił wewnętrznych, to wówczas mówi się o prostym zagadnieniu wytrzymałości pręta. Do zagadnień takich należą:

- rozciąganie i ściskanie - N (tylko siła normalna)

- ścinanie - T (tylko siła tnąca)

- skręcanie - Ms (tylko moment skręcający)

- zginanie - Mg (tylko moment gnący)

5) naprężenie, przemieszczenie, odkształcenie

Założenie o ciągłości materialnych prowadzi do wniosku, że siły wewnętrzne rozłożone są w przekroju w sposób ciągły. Rozpatrujemy punkt B znajdujący się na powierzchni przekroju części (2).

W obrębie przekroju ΔA wydzielonego wokół punktu B siły wewnętrzne redukują się do siły ΔPw.

DEF:

Naprężeniem p w danym punkcie B przekroju danego ciała stałego nazywamy granicę, do której dąży iloraz siły wewnętrznej ΔPw przez wyodrębnione pole ΔA tego przekroju, gdy pole to dąży do zera.

,

Wektor naprężenia można rozłożyć na dwie składowe:

Wyznaczenie rozkładu sił wewnętrznych na powierzchni przekroju określonych wymienionymi naprężeniami jest zadaniem statycznie niewyznaczalnym, a jego rozwiązanie wymaga uwzględnienia odkształceń danego ciała. Wartość naprężenia w danym punkcie ciała zależy nie tylko od obciążenia, ale również od orientacji rozpatrywanego przekroju. Przez każdy punkt można poprowadzić dowolną liczbę przekrojów. Konieczne jest zatem wprowadzenie pojęcia odnoszącego się do ogółu naprężeń.

DEF:

Stanem naprężenia nazywamy ogół naprężeń występujących w różnych punktach i przekrojach rozpatrywanego ciała.

Pod wpływem obciążeń ciało stałe odkształca się, a poszczególne jego punkty przemieszczają się względem określonego układu odniesienia.

DEF:

Przemieszczeniem
punktu M ciała nazywamy wektor, którego początkiem jest ten punkt przed odkształceniem ciała, a końcem punkt M' znajdujący się w nowym położeniu po odkształceniu.

u,v,w - wartości algebraiczne składowych przemieszczenia

- wersowy osi układu

W dalszym ciągu rozważań rozpatrujemy małe przemieszczenia punktów (małe w porównaniu z wymiarami ciała). Podstawowymi wielkościami charakteryzującymi zmiany kształtu ciała są zmiany długości i orientacji odcinków wyznaczonych punktami należącymi do rozpatrywanego ciała. W celu określenia wielkości charakteryzujących lokalny stan odkształcenia weźmy pod uwagę ciało podlegające obciążeniu siłami P₁, P₂, P₃.

Należące do tego ciała dwa punkty A i B znajdujące się w niewielkiej odległości l, po odkształceniu zajmą nowe położenia A' i B' w odległości l'. Pierwotnie prostopadłe osie x,y zmienią orientację i zajmą położenia x', y'.

DEF:

,

- średnie odkształcenie względne na kierunku wyznaczonym przez odcinek AB

- liniowe odkształcenie względne w punkcie A

Odkształcenie
uważamy za dodatnie, gry
, tzn. odległość pomiędzy punktami wzrasta.

DEF:

- kąt odkształcenia postaciowego (wg rysunku) - kąt o jaki zmienia się wzajemne położenie początkowo wzajemnie prostopadłych osi.

Kąt
uważa się za dodatni, gdy kąt pomiędzy osiami maleje po odkształceniu.

Założenia dotyczące sposobu działania sil na konstrukcję:

1. siły przyłożone do konstrukcji wzrastają od zera do swych końcowych wartości w sposób ciągły i powolny

2. w warunkach małych odkształceń i przemieszczeń wartości sił są proporcjonalne do obciążeń, które je spowodowały (obowiązuje liniowo-sprężysty model ciała). Po usunięciu obciążeń ciało powraca do swej pierwotnej postaci

3. działania poszczególnych obciążeń na dany układ sprężysty są od siebie niezależne, w związku z tym wywołane przez nie siły wewnętrzne i odkształcenia można do siebie dodawać, stosując zasadę superpozycji

4. obowiązuje zasada zesztywnienia, zgodnie z którą do zdeformowanego układu materialnego można wykorzystywać ogólne warunki równowagi takie same, jak w przypadku ciała sztywnego. Przy małych deformacjach stosuje się równania równowagi dla położenia konstrukcji w stanie nieodkształconym

5. poprzeczne przekroje prętów płaskie przed odkształceniem pozostają płaskie po odkształceniu (hipoteza płaskich przekrojów Bernoulli'ego)

6. Zasada de Saint-Vernanta

Jeżeli na pewien niewielki obszar ciała sprężystego, pozostającego w równowadze działają kolejno rozmaicie rozmieszczone, ale statycznie równoważne obciążenia, to w odległości od tego obszaru przewyższającej wyraźnie jego rozmiary, powstają praktycznie jednakowe stany naprężenia i odkształcenia.

Istnieją zagadnienia wymagające wprowadzenia dodatkowych założeń lub modyfikacji przedstawionych powyżej (zadania nieliniowo-sprężyste), duże deformacje, naprężenia szybkozmienne, wytrzymałość zmęczeniowa, itp.

2. ROZCIĄGANIE I ŚCISKANIE PRĘTÓW PROSTYCH

1) Związki pomiędzy stanem naprężenia i odkształcenia

1. warunki równowagi - na nieważki pręt prosty o stałym przekroju A działa układ sił lub jedna siła P, która powoduje powstawanie w przekrojach poprzecznych wyłącznie naprężeń normalnych σ.

, jeśli σ = const

2. warunki geometryczne - pod wpływem siły pręt odkształca się. Zgodnie z przyjętymi założeniami, mechanizm deformacji można opisać jako przemieszczenia przekrojów poprzecznych wzdłuż osi pręta przy zachowaniu ich płaskości i prostopadłości do osi.

DEF:

Wydłużenie względne ε zwane również wydłużeniem jednostkowym lub odkształceniem wzdłużnym określone jest wzorem:
. Jak wynika z definicji, jest to wielkość niemianowana. W przypadku ściskania, analogiczną wartość nazywamy skróceniem względnym

Z założenia o płaskości przekroju wynika, że dla danego przekroju poprzecznego ε = const.

Całkowite wydłużenie pręta oblicza się ze wzoru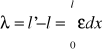
. Przy założeniu, że ε = const(x) otrzymujemy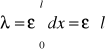
,

Podczas odkształcenia zmieniają się nie tylko wymiary podłużne pręta, ale również jego średnica. Zakładając, że zmiany wymiarów poprzecznych są równomierne, można określić następującą wielkość, zwaną wydłużeniem poprzecznym pręta:
.

W przypadku rozciągania d jest większe od d', czyli ε'<0.

3. związki fizyczne - w celu wyznaczenia wydłużeń, w zależności od wartości obciążenia konieczne jest ustalenie prawa fizycznego dotyczącego związku pomiędzy naprężeniami i odkształceniami.

Prawo Hooke'a

Wydłużenie jest wprost proporcjonalne do naprężenia, które je spowodowało.

E - moduł sprężystości podłużnej (moduł Younga), E [Pa]

Wielkość ta jest cechą danego materiału i charakteryzuje jego odkształcalność.

Wydłużenie poprzeczne jest również proporcjonalne do naprężenia, a stosunek
jest liczbą stałą, zależną od właściwości materiału.

,
[ni] - współczynnik Poissona,

Przy obowiązującym założeniu o płaskości przekrojów, ze związku
wynika, że naprężenie σ musi mieć wartość stałą w danym przekroju, a zatem z równania
wynika związek
.

Wydłużenie całkowite wyznaczone ze wzoru
, po uwzględnieniu powyższych związków wynosi
, EA - sztywność pręta na rozciąganie

2) Statyczna próba rozciągania

Uważana jest za podstawowe doświadczenie w wytrzymałości materiałów, mające doprowadzić do określenia właściwości mechanicznych materiału. Próba realizowana jest przy użyciu maszyny wytrzymałościowej, zwanej zrywarką. Specjalna próbka poddawana jest rozciąganiu siłą, której wartość wzrasta powoli z prędkością określoną odpowiednią normą. Zakłada się, że odpowiadające określonym naprężeniom odkształcenia pojawiają się natychmiast po zadziałaniu obciążenia, czyli w każdym momencie istnieje równowaga w stanie naprężenia i odkształcenia. Próbę poprzedza dokładny pomiar charakterystycznych wymiarów próbki.

S₀, S_n - wielkości przekroju poprzecznego przed i po odkształceniu

W wyniku próby otrzymujemy wykres zależności P-Δl, gdzie P - siła rozciągająca

W celu umożliwienia porównania otrzymanych wyników, dla różnych materiałów i różnych rozmiarów próbek, przedstawia się otrzymaną zależność w układzie σ-ε.

.

Dla większości materiałów w początkowym stadium próby aż do przekroczenia przez siłę rozciągającą pewnej granicznej wartości, zależność jest liniowa (odcinek 0A). Obowiązuje tu prawo Hooke'a.

- granica proporcjonalności: największa wartość naprężenia, przy której zachodzi jeszcze wprost proporcjonalna zależność pomiędzy wydłużeniem i naprężeniem - granica stosowalności prawa Hooke'a.

Dalszemu wzrostowi obciążenia towarzyszy coraz szybszy przyrost odkształcenia, a wykres przybiera postać łuku. Po przekroczeniu wartości siły odpowiadającej punktowi B, próbka doznaje odkształceń trwałych.

- granica sprężystości: największa wartość naprężenia, przy której nie zachodzą jeszcze odkształcenia trwałe.

Ze względu na trudności w oddzielnym pomiarze powyższych wielkości przyjmuje się tzw. umowną granicę sprężystości.

- wartość siły odpowiadająca odkształceniu trwałemu o 0,05%

W przypadku stosowania umownej granicy sprężystości, jest ona kresem stosowalności prawa Hooke'a.

Po przekroczeniu wartości siły odpowiadającej punktowi C wykresu, materiał osiąga stan płynięcia, doznając przyrostów wydłużenia przy braku przyrostów siły.

- granica plastyczności - wartość naprężenia, przy której próbka zaczyna doznawać przyrostu odkształcenia przy braku przyrostu obciążenia.

Charakterystyka σ-ε na odcinku CD jest pofalowana wskutek pojawiających się poślizgów pomiędzy cząstkami materiału. W związku z tym Polska Norma określa pojęcie górnej i dolnej granicy plastyczności.

Dla celów praktycznych definiuje się wielkość nazywaną umowną granicą plastyczności

- wartość siły odpowiadająca odkształceniu trwałemu o 0,2%

Do dalszej deformacji próbki konieczny jest przyrost obciążenia.

- wytrzymałość na rozciąganie: wartość naprężenia odpowiadająca maksymalnej wartości siły rozciągającej próbkę.

W ostatniej fazie eksperymentu na próbce pojawia się przewężenie. Jej rzeczywisty minimalny przekrój poprzeczny jest zatem znacznie mniejszy niż wartość S₀. Linia DE' wykresu odpowiada naprężeniu rzeczywistemu, tj. odniesionemu do rzeczywistego, aktualnego pola powierzchni przekroju poprzecznego.

3) Naprężenia dopuszczalne - współczynnik bezpieczeństwa

Wzrost naprężeń i związanych z nimi odkształceń powoduje zmiany w stanie fizycznym ciała, które prowadzą do odkształceń trwałych lub zniszczenia spójności materiału. Zmiany te określa się jako wytężenie materiału. Wzrost wytężenia jest miarą „wyczerpywania się” zapasów wytrzymałości materiałów. W przypadku rozciągania lub ściskania prętów prostych miarą wytężenia jest naprężenie normalne σ w przekroju poprzecznym pręta.

W poprawnie zaprojektowanej konstrukcji wytężenia nie może osiągnąć stanu niebezpiecznego, a zatem w przypadku pręta rozciąganego naprężenie σ nie może osiągnąć wyznaczonej eksperymentalnie wartości niebezpiecznej, za którą w zależności od warunków można uznać granicę plastyczności R_e, wytrzymałość na rozciąganie R_M lub wytrzymałość na zmęczenie.

DEF:

Maksymalną wartość, jaką może osiągnąć naprężenie σ nazywamy naprężeniem dopuszczalnym.

n - współczynnik bezpieczeństwa; n > 1

kr - wytrzymałość dopuszczalna na rozciąganie

kc - wytrzymałość dopuszczalna na ściskanie

Właściwy dobór współczynnika bezpieczeństwa jest jednym z podstawowych zagadnień w procesach projektowania elementów konstrukcji. Jego wartość musi być na tyle duża, by uwzględnić prawdopodobieństwo zupełnie przypadkowych odstępstw od warunków przyjętych za podstawę obliczeń. Przyjęcie zbyt dużej jego wartości prowadzi z kolei do przewymiarowania konstrukcji i związanego z tym zbędnego przyrostu jej masy oraz nadmiernej materiałochłonności.

Podstawą obliczeń prętów poddanych działaniu siły osiowej jest równanie

Warunek wytrzymałościowy

Warunek sztywnościowy:

Całkowite wydłużenie (skrócenie) pręta nie może przekroczyć wartości dopuszczalnej, umożliwiającej poprawną pracę elementów konstrukcji:

3. STAN NAPRĘŻENIA

1. Oznaczenia składowych naprężeń. Tensor naprężeń.

W celu określenia stanu naprężenia w ciele konieczna jest znajomość naprężenia w dowolnym przekroju ciała w dowolnym jego punkcie. W celu oznaczenia składowych stanu naprężenia w punkcie wyodrębnia się wokół niego nieskończenie mały prostopadłościan, nazywany prostopadłościanem elementarnym.

Jeżeli wymiary badanego prostopadłościanu są nieskończenie małe, to jednoimienne i równoległe naprężenia dla każdej pary ścian równoległych różnią się o nieskończenie małą wartość, a zatem można przyjąć, że są jednakowe.

- naprężenia styczne

W prostopadłościanie elementarnym występuje 9 składowych naprężeń: 3 normalne i 6 stycznych.

TW.

Składowe naprężeń stycznych prostopadłe do krawędzi przecięcia się dwóch przekrojów elementarnych, wzajemnie prostopadłych są zawsze równe. Oznacza to, że:

Składowe naprężenia określające stan naprężenia w rozpatrywanym punkcie można przedstawić w postaci macierzy, zwanej tensorem naprężeń:

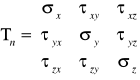
Można zatem stwierdzić, że stan naprężenia w punkcie jest w pełni określony, jeżeli znany jest tensor naprężeń dla tego punktu.

Dla każdego określonego stanu naprężenia można wyznaczyć trzy wzajemnie prostopadłe osie określające trzy kierunki główne. W odpowiadających im przekrojach występują wyłącznie naprężenia normalne zwane głównymi. Orientacja kierunków głównych oraz wartości naprężeń głównych nie są zależne od przyjętego, wyjściowego układu współrzędnych i są niezmiennikami stanu naprężenia.

Znajomość kierunków naprężeń głównych umożliwia określenie stanu naprężenia tylko trzema składowymi. Wartości naprężeń głównych spełniają nierówności:

- naprężenie maksymalne

- naprężenie minimalne

2. Płaski stan naprężenia

Jeżeli jedno z naprężeń głównych jest równe zeru, to stan naprężenia nazywamy płaskim. Płaski stan naprężenia występuje np. w każdym obciążonym przedmiocie w jego warstwie zewnętrznej, wolnej od bezpośredniego działania sił zewnętrznych.

Rozpatrujemy prostokątny wycinek ciała o określonej grubości, w którym panuje jednorodny, płaski stan naprężeń.

Umowa co do znaków naprężeń:

- normalne σ jest dodatnie, jeżeli jest rozciągające

- styczne
jeżeli naprężenie styczne na boku o normalnej zewnętrznej odpowiadającej jednej z osi układu YZ ma zwrot zgodny ze zwrotem drugiej osi układu, to jest ono naprężeniem dodatnim.

3. Własności składowych płaskiego stanu naprężenia:

1. naprężenia normalne i styczne w przekrojach równoległych są sobie równe:

2. naprężenia styczne w dwóch wzajemnie prostopadłych przekrojach są równe co do wartości liczbowej i skierowane do wspólnego naroża i od wspólnego naroża.

3. suma naprężeń normalnych w dwóch wzajemnie prostopadłych przekrojach jest niezmiennikiem układu

4. jeżeli znane są naprężenia normalne w dwóch wzajemnie prostopadłych przekrojach oraz naprężenia styczne w jednym z nich, to stan naprężenia jest jednoznacznie określony.

4. Koło Mohra dla płaskiego stanu naprężenia

a) D:
Sz:

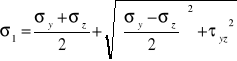
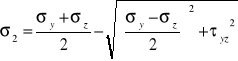
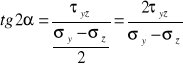
b) D:
Sz:

5. Odkształcenia w płaskim stanie naprężenia

Rozpatrujemy kostkę sześcienną o wymiarach jednostkowych, poddaną działaniu płaskiego stanu naprężenia. Stosując zasadę superpozycji, powyższy stan naprężenia można wyrazić jako dwa stany składowe:

Odkształcenia kostki poddanej jednorodnemu działaniu naprężeń σ₁, σ₂ są superpozycją odkształceń w obu powyższych stanach.

- uogólnione prawo Hooke'a dla płaskiego stanu naprężeń

Analogicznie dla kostki jednostkowej poddanej trójkierunkowemu stanowi naprężeń otrzymujemy:

uogólnione prawo Hooke'a wyrażone poprzez naprężenia główne

6. Uproszczona analiza trójwymiarowego stanu naprężeń

Rozpatrujemy kostkę sześcienną poddaną działaniu naprężeń głównych
, przy czym zachodzą nierówności:
.

Trójwymiarowy stan naprężenia można potraktować jako superpozycję trzech stanów płaskich dla trzech wzajemnie prostopadłych płaszczyzn. W każdym z tych przypadków stan naprężenia możemy zilustrować za pomocą koła Mohra.

Można udowodnic, że przy równoczesnym działaniu wszystkich trzech naprężeń głównych, naprężenia w dowolnym przekroju określone będą odpowiednim punktem N, znajdującym się w obszarze zakreskowanym, ograniczonym trzema kołami Mohra, zbudowanymi dla naprężeń głównych.

Wartości naprężeń w przekroju o normalnej n określone są przez punkt N na rysunku. Największe naprężenie styczne
wystepuje w przekroju prostopadłym do płaszczyzny wyznaczonej przez kierunki naprężeń głównych
i
, a normalna tego przekroju tworzy kąt 45° z kierunkami naprężeń
i
.

4. HIPOTEZY WYTRZYMAŁOŚCIOWE

- naprężenie zredukowane

Hipotezy wytrzymałościowe są formułami określającymi kryteria oceny stanu wytężenia materiału w złożonym (trójwymiarowym) stanie naprężenia w celu ilościowego porównania takiego stanu przypadkiem prostym, jakim jest rozciąganie.

Naprężeniem zredukowanym
(
) nazywamy naprężenie otrzymane po zastosowaniu przyjętej hipotezy wytrzymałościowej dla trójkierunkowego stanu naprężenia, które jest równoważne z naprężeniem rozciągającym w jednowymiarowym stanie naprężenia.

1) hipoteza
(Rauchine'a)

W myśl tej hipotezy naprężenia
i
nie mają żadnego wpływu na wytężenie materiału. Hipoteza ta ma znaczenie historyczne, bywa czasem stosowana dla materiałów kruchych.

2) hipoteza największego wydłużenia względnego
(de Saint Vernanta)

Hipoteza ta daje lepszą zgodność z wynikami doświadczeń od hipotezy
. Była powszechnie stosowana w początkach XX w., obecnie stosowana dla niektórych materiałów kruchych.

3) hipoteza największych naprężeń stycznych
(Coulomba)

Hipoteza wykazuje dużą zgodność z doświadczeniem (szczególnie dla materiałów plastycznych) i bywa obecnie szeroko stosowana.

4) hipoteza Huber-Mises-Henckig (H-M-H)

W myśl tej hipotezy o wytężeniu materiału decyduje największa energia odkształcenia postaciowego.

Wartość wynikająca z hipotezy Hubera wykazuje największą zgodność z wynikami doświadczeń dotyczących materiałów plastycznych wykazujących jednakowe własności na rozciąganie i ściskanie (stale, stopy miedzi, aluminium, itp.)

Hipoteza
bywa stosowana na równi z hipotezą Hubera, ponieważ w większości przypadków obie hipotezy dają zbliżone wyniki. Hipoteza jest przy tym łatwiejsza w stosowaniu ze względu na prostotę formuły określającej naprężenie zredukowane.

5. ZGINANIE PROSTE

Rozpatrujemy dowolny przekrój poprzeczny pręta obciążonego układem sił zewnętrznych. Jako biegun redukcji sił zewnętrznych przekroju przyjmujemy punkt 0.

Jeżeli siły wewnętrzne redukują się do wektora momentu gnącego Mg, to mówimy że w przekroju tym występuje czyste zginanie.

Jeżeli oprócz momentu gnącego w przekroju występuje również siła tnąca T, to mamy do czynienia z przypadkiem zginania z udziałem sił poprzecznych.

Jeżeli siła tnąca oraz para sił, efektem której jest moment gnący, występują w jednej płaszczyźnie zawierającej osie główne centralne przekrojów poprzecznych pręta, to zginanie takie nazywamy płaskim (prostym).

Jeżeli siły czynne i ich reakcje działające na pręt zginany leżą w jednej płaszczyźnie, to płaszczyznę tę nazywamy płaszczyzną zginania.

Zginanie płaskie występuje zatem wówczas, gdy płaszczyzna zginania pokrywa się z płaszczyzną główną zawierającą oś pręta, stanowiącą miejsce geometryczne środków ciężkości przekrojów poprzecznych pręta. W takim przypadku oś pręta poddanego zginaniu pozostaje nadal w tej płaszczyźnie.

W przypadku przeciwnym mamy do czynienia z tzw. zginaniem ukośnym, gdzie oś pręta staje się po odkształceniu krzywą w przestrzeni.

Dla potrzeb obliczeń wytrzymałościowych belkę rzeczywistą zastępujemy modelem, w którym wektor momentu gnącego prostopadły do płaszczyzny zginania zastępujemy łukiem leżącym w płaszczyźnie zginania.

Rozpatrujemy belkę obciążoną pojedynczą siłą poprzeczną P.

Aby zapewnić równowagę statyczną myślowo wyodrębnionemu fragmentowi pręta, w jego przekroju poprzecznym określonym współrzędną x musi wystąpić siła tnąca T równoważąca reakcję na końcu wyodrębnionego odcinka oraz moment gnący Mg równoważący efekt działania powstałej pary sił. W świetle powyższego przykładu, ograniczając rozważania do układu sił działających w jednej płaszczyźnie zawierających oś belki, można sformułować następujące definicje poszczególnych składowych obciążenia:

1. siłą tnącą T w danym przekroju poprzecznym belki nazywamy siłę równoważącą płaszczyznę tego przekroju wypadkowej wszystkich sił zewnętrznych działających na część belki odciętą w tym przekroju

2. momentem gnącym Mg w danym przekroju belki nazywamy moment równoważący siłę momentów wszystkich sił zewnętrznych działających na część belki odciętą tym przekrojem

Moment gnący uważamy za dodatni, jeżeli stara się wygiąć wyodrębniony myślowo element belki wypukłością w dół (w stronę dodatniego zwrotu osi y). Siła tnąca posiada znak zgodny ze znakiem Mg, jeżeli współrzędna x odmierzana jest zgodnie ze zwrotem osi x. W przeciwnym wypadku znaki Mg i T są różne.

Model belki zginanej może być obciążony za pomocą skupionych sił poprzecznych, rozłożonych obciążeń poprzecznych oraz skupionych momentów gnących.

Rozpatrujemy belkę obciążoną w sposób dowolny:

Można wykazać, że dla dowolnego przekroju poprzecznego belki, określonego współrzędną x, słuszne są następujące związki:

Analiza naprężeń i odkształceń pręta zginanego

Rozpatrujemy pręt o prostokątnym przekroju poprzecznym, poddany czystemu zginaniu:

W odkształconym pręcie przekroje poprzeczne płaskie przed odkształceniem pozostają płaskie po odkształceniu. Włókna D, D₁ ulegają wydłużeniu, a włókna B, B₁ - skróceniu. Długości włókien C, C₁ położonych w połowie przekroju nie ulegają zmianie. W strefie włókien B, B₁ pręt ulegnie rozszerzeniu, a w strefie włókien D, D₁ - zwężeniu. Pierwotnie prostokątny przekrój poprzeczny przybierze kształt zbliżony do trapezowego.

Oprócz hipotezy płaskich przekrojów, w mocy pozostaje druga hipoteza stwierdzająca, że względne odkształcenia poprzeczne pręta są w każdym punkcie
-razy mniejsze od odkształceń podłużnych, zatem związek pomiędzy odkształceniami jest identyczny, jak w przypadku zwykłego rozciągania lub ściskania. Zakłada się, że włókna równoległe do osi pręta poddawane są jednokierunkowemu stanowi naprężenia i nie wykazują żadnych wzajemnych oddziaływań poprzecznych. Włókna położone w poziomej płaszczyźnie symetrii nie ulegają ani skróceniu, ani wydłużeniu, a zatem naprężenia w tych włóknach są równe zero. Powierzchnię utworzoną z tych włókien nazywamy warstwą obojętną. Krawędź przecięcia się warstwy obojętnej z płaszczyzną przekroju poprzecznego pręta zginanego nazywamy osią obojętną tego przekroju.

Długość odcinka
po deformacji nie uległa zmianie i wynosi
. Włókno
przed odkształceniem miało długość równą
, natomiast po odkształceniu:
.

Wydłużenie względne włókna wynosi:

Zgodnie z prawem Hooke'a, włókno to rozciągane jest naprężeniem
, więc

Promień krzywizny ρ jest stały, a zatem naprężenia w poszczególnych punktach przekroju belki zginanej zmieniają się proporcjonalnie do odległości tych punktów od warstwy obojętnej.

Naprężenia te muszą zapewniać równowagę statyczną rozpatrywanej części pręta.

Elementarna siła wynosi

Po podstawieniu zależności
, otrzymujemy:

Z warunku równowagi statycznej wynika, że suma sił elementarnych w całym przekroju pręta równa się 0.

Ponieważ
, zatem równanie jest spełnione gdy
, a zatem gdy moment statyczny pola przekroju względem osi obojętnej jest równy 0.

Oznacza to, że oś obojętna przekroju musi pokrywać się z jego osią centralną, a zatem warstwa obojętna przechodzi przez środki ciężkości przekrojów poprzecznych. Ze względu na małe odkształcenia, przyjmuje się że oś obojętna jest prostą, a warstwa obojętna - powierzchnią walcową.

Moment elementarnej siły dM względem osi obojętnej wynosi
.

Z warunku równowagi momentów dla rozpatrywanej części otrzymujemy:

Z zależności
oraz powyższej otrzymujemy:

Uwzględniając, że
, otrzymujemy:

Z równania
otrzymujemy

Porównując stronami powyższe równania, otrzymujemy: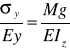
, ostatecznie:

- naprężenie normalne w dowolnym punkcie przekroju

Z powyższego wyrażenia wynika, że największe wartości przyjmują naprężenia w włóknach najbardziej oddalonych od osi obojętnej. Jeżeli odległości skrajnych włókien ściskanych i rozciąganych od osi obojętnej są równe, to wartości największych naprężeń rozciągających i ściskających są równe. Dla uproszczenia nazywamy je naprężeniami gnącymi.

- naprężenie gnące

Wprowadźmy oznaczenie:
(wskaźnik wytrzymałości przekroju na zginanie)

k_g - wytrzymałość dopuszczalna na zginanie

- jeżeli
, to

- jeżeli
, to:

,
,

,
,

Wykresy momentów gnących i sił tnących

W przypadku ogólnym zginania z udziałem sil poprzecznych, wartości momentów gnących i sił tnących są zmienne. Przebiegi ich zmienności można zilustrować graficznie za pomocą odpowiednich wykresów. Wykres momentów gnących jest graficzną ilustracją funkcji opisujących zmiany wartości momentu gnącego w poszczególnych przekrojach belki zginanej. Odpowiednio wykres sił tnących opisuje przebieg zmienności funkcji opisujących zmiany siły tnącej. Aby mógł zostać sporządzony wykres sił tnących, muszą być znane wartości wszystkich sił obciążających belkę. Sporządzenie wykresu momentów gnących wymaga znajomości wartości wszystkich sił i momentów obciążających belkę oraz znajomości przebiegu zmienności sił tnących. Zależność pomiędzy wartościami sił tnących i momentów gnących opisuje formuła:

---