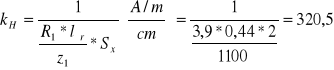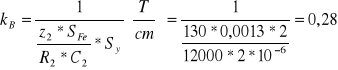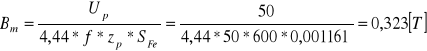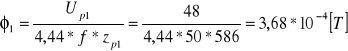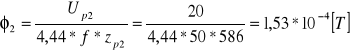|
LABORATORIUM ELEKTROTECHNIKI
|
|
|
|
|
|
|
|
|
|
|
|
|
|
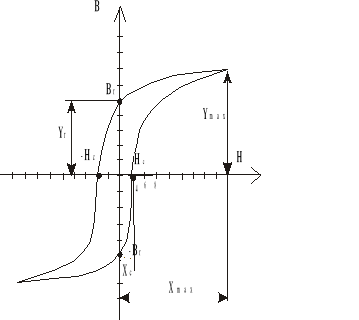
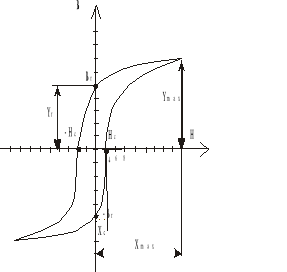
1. Wyznaczenie dynamicznej charakterystyki magnesowania.
|
|
Średnia długość linii strumienia w rdzeniu
|
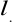
= 44 cm
|
Rezystancja opornika pomiarowego
|
|
Liczba zwojów uzwojenia wzbudzającego
|
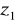
=1100
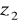
=130
|
Parametr układu całkującego
|
|
Czułość wejścia „X” oscyloskopu
Czułość wejścia „Y” oscyloskopu
|
|
Bmax=kB*ymax Br=kB*yr Hmax=kH*xmax Hc=kH*xc
Bmax=7,9542 [T] Br=2,84 [T] Hmax=11538 [A/m] Hc=1282 [A/m]
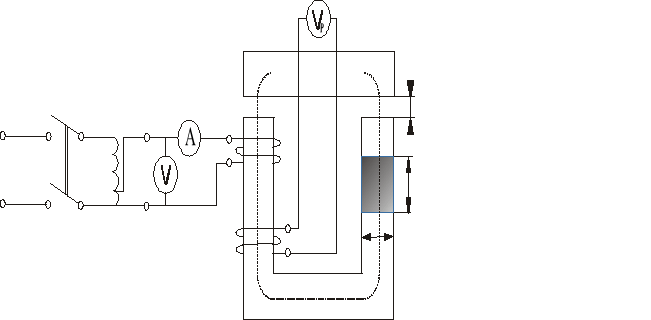
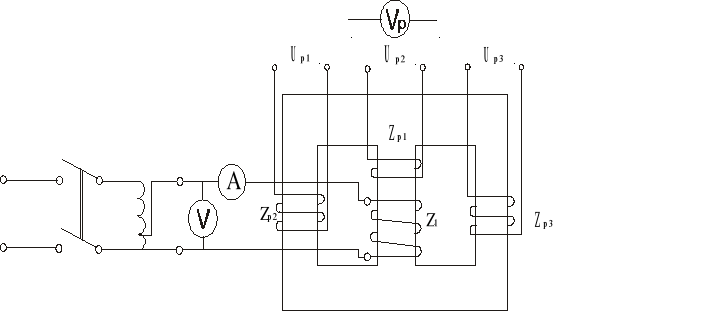
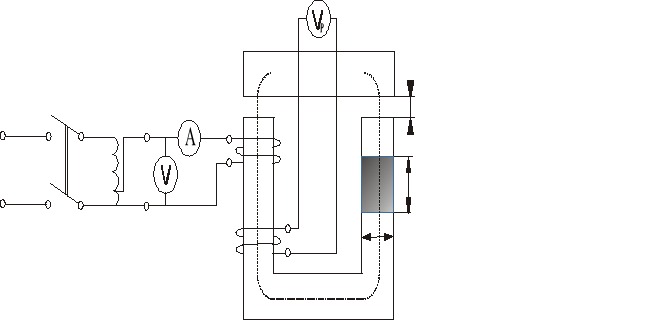
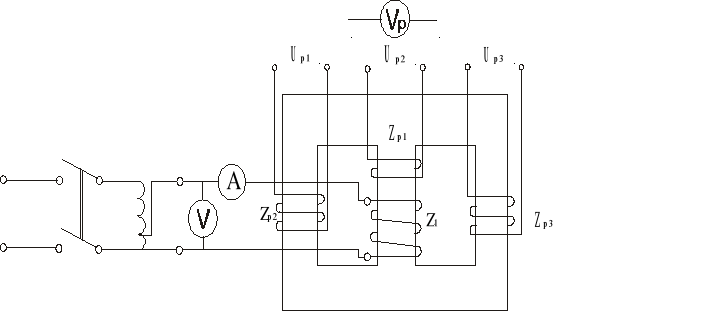
2. Badanie nie rozgałęzionego obwodu magnetycznego.
Wyznaczanie charakterystyki magnesowania prądem przemiennym
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
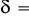
0,3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
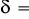
0,7
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

3. Badanie rozgłęzionego obwodu magnetycznego.
woltomierz elektromagnetyczny kl. 0,5
amperomierz elektromagnetyczny kl. 0,5
- Sprawdzanie I prawa Kirchhoffa
I prawo Kirchhoffa dotyczy bilansu strumieni w węźle. Suma algebraiczna strumieni w węźle obwodu magnetycznego równa jest zeru 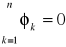
- Sprawdzanie II prawa Kirchhoffa
II prawo Kirchhoffa określa bilans napięć magnetycznych w oczku obwodu. Suma algebraiczna napięć magnetycznych w zamkniętym obwodzie magnetycznym równa się sumie sił magnetomotorycznych (amperozwojów) działających w tym obwodzie:
- Obliczanie parametrów schematu zastępczego i sprawdzanie I prawa Kirchhoffa.
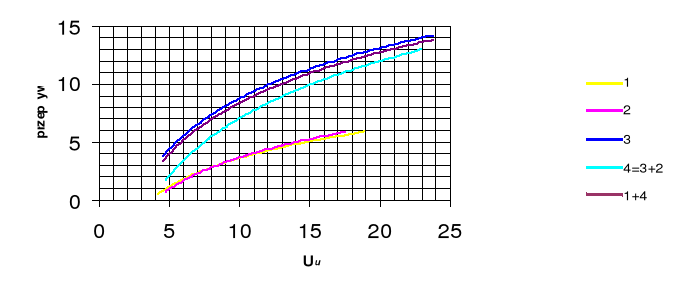
- Wyznaczani graficzne charakterystyki Ф=f(I*z) obwodu.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
|
|
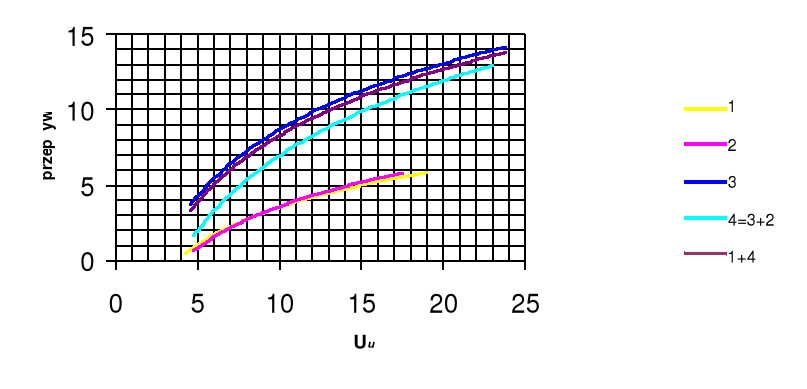
Charakterystyki poszczególnych gałęzi:
Charakterystyka łączna: 1+4 - 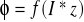
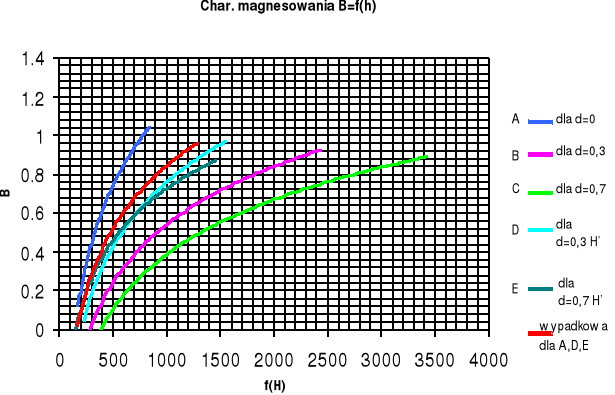
Nierozgałęziony obwód magnetyczny:
Wraz ze wzrostem szerokości szczeliny wzrasta wartość natężenia H przy tej samej wartości napięcia zasilającego
Wraz ze wzrostem szerokości szczeliny wzrasta wartość przepływającego prądu elektrycznego
Wartość indukcji magnetycznej nie zależy od szerokości szczeliny (dla niewielkich szczelin δ<0,2*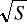
)
Wraz ze wzrostem szerokości szczeliny napięcie wyjściowe maleje, więc można stwierdzić, że zostaje odkładane na szczelinie
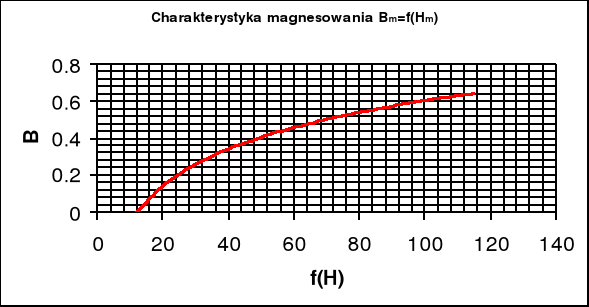
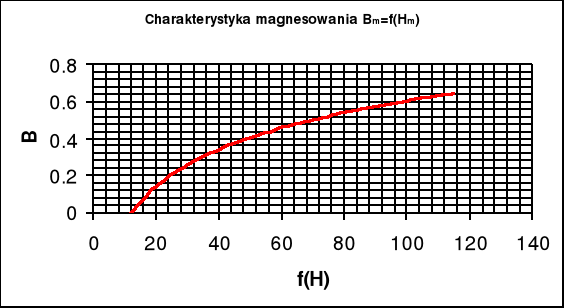
Jak wynika z charakterystyki magnesowania Bm=f(Hm) wraz ze wzrostem natężenia magnetycznego rośnie indukcja magnetyczna (zależność logarytmiczna). Im większa szczelina jest większa tym wykres char-ki jest pod mniejszym kątem do osi Hm
Obwód ze szczeliną możemy rozwiązać metodą graficzną, znając char-kę rdzenia (δ=0), oraz char-kę szczeliny.
Znajdując char-kę wypadkową otrzymujemy charakterystykę dla obwodu ze szczeliną
Rozgałęziony obwód magnetyczny
1) W doświadczeniu sprawdzającym I prawo Kirchoffa można przyjąć, że prawo to jest potwierdzone, ponieważ suma strumieni w węźle , odpowiednio dla przypadków, równa się A: 0,45*10-4 ; B: 0,92*10-4 ; C: 1,08*10-4
a bezwzględny błąd wynosi
A: =10,9 %; B: = 8 %; C: =7,8 %
a więc mieści się w granicy błędu, który wynosi 15%
2) W doświadczeniu dotyczącym II prawa Kirchhoffa bezwzględny błąd jest dosyć duży i wynosi (odpowiednio);
A: =22 % ; B: =48 % ; C: =47 %
Ten duży błąd spowodowany jest m.in.:
wydzieleniem energii cieplnej na cewce i w rdzeniu
rozproszeniem strumienia poza rdzeń w cewce zasilającej
występowaniem prądów wirowych
Obliczanie parametrów obwodu zastępczego
Obwód magnetyczny można traktować zastępczy jako nieliniowy obwód elektryczny
potwierdza to doświadczenie w którym obliczamy parametry schematu zastępczego i sprawdzamy I prawo Kirchhoffa. Jest ono słuszne gdyż suma strumieni w gałęziach przy zadanym wymuszeniu jest w przybliżeniu równa zeru( dla wszystkich przyp.) A,B,C=0,1*10-4 ; a bezwzględny błąd wynosi A: =17 %; B: =14 %; C: =13% (mieści się w granicy błędu)
z tych rozważań możemy wysnuć wniosek, że prawo Kirchhoffa możemy stosować dla obwodów magnetycznych przy teoretycznym rozpatrywaniu obwodu, w praktyce musimy uwzględnić błędy przytoczone w punkcie c).
![]()
![]()
![]()