Kiniuś™
Statystyka
Dr Elżbieta Grabowska
(notatki z wykładu 4)
27.03.2009 (piątek)
ŚREDNIA DLA INDYWIDUALNYCH DANYCH ILOŚCIOWYCH
![]()
lub ![]()
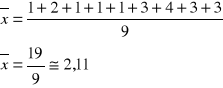
( powyższy przykład do danych z poprzedniego wykł. ile długopisów…)
![]()
jest najdokładniejszą miarą położenia i tendencji centralnej zbioru danych, ale jako miara klasyczna (wynik zależy od wszystkich pomiarów) jest wrażliwa na wyniki przypadkowe, wyniki nietypowe, nietypowy rozkład danych.
![]()
- średnia zawsze zawiera się między minimalną a maksymalną wartością zbioru danych
![]()
- zawsze dąży do zera
Średnia dla nietypowego rozkładu danych
1. Rozkład ekstremalnie skośny
1, 1, 1, 1, 1, 1, 1, 1, 30, 50.
Me -1
D - 1
![]()
- 8,8 - niewiarygodna średnia
(firma ma 10 pracowników 8 z nich zarabia po 1 tys. złotych, jeden pracownik zarabia 30 tys. i jeden 50 tys. Średnia to 8,8 tys. Ale to nie znaczy że każdy pracownik zarabia po ok.8,8 tys.)
2. Rozkład siodłowy
dla danych siodłowych ![]()
jest niewiarygodne i jej liczenie nie ma sensu…
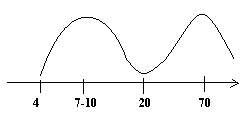
Oglądalność programu `ziarno'
średnia arytmetyczna wieku to 20,8.
Jak widać na wykresie około 20 roku życia oglądalność tego programu jest najmniejsza - średnia nie wiarygodna.
Kiniuś™
3. Rozkład normalny
Jeżeli rozkład danych jest typowy to mediana równa jest dominancie i średniej.
Me = D = ![]()
Im bardziej rozkład danych jest nietypowy tym bardziej wartości tych miar się rozbiegają.
WSKAŹNIKI POŁOŻENIA DLA DANYCH ILOŚCIOWYCH POGRUPOWANYCH W SZEREG PUNKTOWY
Średnia dla danych punktowych
Jeżeli danych jest dużo, a cecha ma charakter skokowy to wyniki grupujemy w szereg rozdzielczy, punktowy.
|
|
|
0 1 2 3 |
2 2 7 4 |
0 2 14 12 |
|
15 |
28 |
![]()
- warianty cechy
![]()
- liczba przypadków każdego wariantu
mierzona cecha: liczba posiadanych zwierząt domowych.
D - 2 (7 osób posiada 2 zwierzątka domowe)
![]()
(suma ni równa jest liczebności próby)
![]()
lub 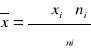
![]()
Wniosek:
Przeciętnie na jedną osobę z badanej grupy przypada 1,87 zwierzaka domowego.
Dominanta dla danych punktowych
Dominantą jest wariant cechy, który
wskazuje największą liczebność cząstkową.
|
|
1 2 3 4 |
7 7 8 7 |
|
|
1 2 3 4 |
2 3 3 2 |
Dominanta to 3 !
Brak dominanty
Kiniuś™
Mediana dla danych punktowych
1) Wyznaczamy pozycję mediany
Uwaga!!!
Przy dużych danych przyjęte jest:
![]()
dla danych nieparzystych
![]()
dla danych parzystych
2) Kumulujemy szereg liczebności
3) Wskazujemy palcem medianę
Wariant cechy na wysokości którego pozycja mieści się w liczebności skumulowanej
Przykład 1
|
|
ncum |
0 1 2 3 |
2 2 7 4 |
2 4 11 15 |
|
N=15 |
|
![]()
ncum - liczebność skumulowana, liczona narastająco
Poz.Me=8 mieści się w 11, czyli Me=2
Prawidłowe skumulowanie gdy:
Ostatnia pozycja w szeregu skumulowanym, jest równa liczebności próby.
Wniosek:
Połowa grupy ma, co najwyżej 2 zwierzaki domowe (2 lub mniej), i połowa grupy ma co najmniej 2 zwierzaki domowe (2 lub więcej).
Przykład 2
|
|
|
ncum |
2 3 4 5 |
10 3 3 3 |
20 9 12 15
|
10 13 16 10 |
|
N=19 |
56 |
|
![]()
![]()
Poz.Me=10 mieści się w 10, czyli Me=2
Uwaga! Dane ujęte jako indywidualne i dane ujęte w szereg punktowy, daja identyczne wskaźniki.
Kiniuś™
Przykład 3
Cecha mierzona: liczba posiadanych bratanków.
|
|
|
ncum |
0 1 2 3
|
20 21 7 2 |
20 21 14 6
|
20 41 48 50 |
|
N=50 |
|
|
D = 1 Typowe jest posiadanie jednego bratanka
![]()
Przeciętnie na 1 os. przypada 0,82 bratanka.
![]()
Me=1
Wniosek:
Połowa grupy ma co najwyżej 1 bratanka, a połowa ma co najmniej 1 bratanka.
WSKAŹNIKI POŁOŻENIA DLA DANYCH ILOŚCIOWYCH UJĘTYCH W SZEREG ROZDZIELCZY KLASOWY
Jeżeli danych jest dużo, a cecha ma charakter ciągły (lub danych jest bardzo dużo i cecha jest skokowa) to opłaca się zestawić dane w szereg rozdzielczy klasowy.
|
|
|
00-10 10-20 20-30 30-40 |
2 5 8 2
|
5 15 25 35 |
|
N=17 |
|
Jest to szereg klasowy uproszczony.
Cechy:
górna granica poprzedniego przedziału jest równa dolnej kolejnego.
mają równe przedziały
- środek przedziału.
|
|
00,00-09,99 10,00-19,99 20,00-29,99 30,00-39,99 |
2 3 6 2 |
|
|
00,1-10,00 10,1-20,00 20,1-30,00 30,1-40,00 |
2 3 6 2 |
Są to dwa przykłady na szereg klasowy dokładny
(Dane zapisujemy w uproszczonym szeregu w domyśle stosujemy jeden z dwóch szeregów dokładnych)
Uwaga! Dane z szeregu klasowego będą zawsze przybliżone i zaokrąglone.
Różnice w stosunku do danych indywidualnych będą tym większe im szersze przyjmiemy przedziały.
Kiniuś™
Średnia dla danych klasowych
![]()
lub 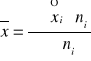
|
|
|
|
00-10 10-20 20-30 30-40 |
2 5 8 2
|
5 15 25 35 |
10 75 200 70 |
|
N=17 |
|
355 |
![]()
Dominanta dla danych klasowych
Dominantę można wyznaczyć tylko w przybliżeniu pod warunkiem, że są spełnione 3 warunki:
musi być jeden przedział dominujący
przedział ten nie może być ani pierwszy ani ostatni
rozpiętość 3 przedziałów kluczowych ( dominującego i dwóch sąsiednich) musi być jednakowa
D dla danych klasowych można wyznaczyć:
a) ze wzoru interpolacyjnego
![]()
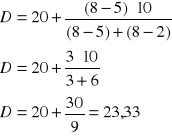
xo - dolna granica przedziału dominującego
nD - liczebność przedziału nominacyjnego
nD-1- liczebność przedziału poprzedniego (przed dominującym)
nD+1- liczebność przedziału następnego (po dominującym)
hD - rozpiętość przedziału dominującego
Uwaga!
Obliczona dominanta musi się mieścić w przedziale dominującym.
Kiniuś™
b) graficznie
rysujemy histogram
łączymy na krzyż rogi słupków, ze skrzyżowania spuszczamy linię do osi x
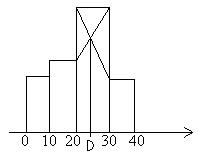
|
|
05-15 15-25 25-35 |
2 6 2 |
![]()
Symetryczny rozkład danych
D=20 Me=20 x=20
Mediana dla danych klasowych
Wyznaczanie:
Medianę można wyznaczyć zawsze, nie ma takich danych, dla których nie można by było wyznaczyć Me.
Wyznaczamy pozycję mediany ze wzoru:
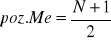
Kumulujemy szereg liczebności
Ustalamy, w którym miejscu szeregu skumulowanego mieści się pozycja
Wartość mediany wyznacza się ze wzoru interpolacyjnego:
![]()
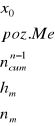
- dolna granica przedziału medialnego
- pozycja mediany
- liczebność skumulowana poprzedzająca przedział mediany
- rozpiętość przedziału medialnego
- liczebność przedziału medialnego
Kiniuś™
Rozkład typowy
|
|
ncum |
00-10 10-20 20-30 30-40 |
2 5 8 2 |
2 7 15 17 |
|
N=17 |
|
ncum = N
Poz.Me = (17+1):2=9
x0 = 20 nm = 8
hm = 10 nasza Poz.Me=9 mieści się w ncum=15
![]()
Obliczona wartość Me musi się mieścić w przedziale medialnym!
Wniosek:
Połowa grupy wydała, co najwyżej 20,50 zł (lub mniej) i połowa grupy wydała conajmnie22,50 (lub więcej).
Rozkład danych zbliżony do typowego:
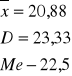
Liczenie Me dla danych nietypowych
Cecha mierzona:
Wielkość posiadanej działki w arach.
|
|
|
|
|
0,2-1,0 1,1-2,1 2,2-10 10,1-20,3 |
30 12 5 5 |
0,6 1,6 6,1 15,2 |
18 19,2 30,5 76 |
30 42 47 52 |
|
N=52 |
|
143,7 |
|
Dla takich danych nie można wskazać D, bo nie ma równych przedziałów i przedział dominujący jest pierwszy.
![]()
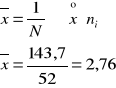
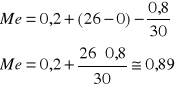
Wniosek:
Połowa właścicieli ma działki o powierzchni, co najwyżej 0,89 (lub mniejsze) i połowa ma działki o wielkości, co najmniej 0,89 (lub większe).
7
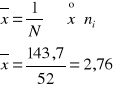
Wyszukiwarka
Podobne podstrony:
7136 TSCM 52 2 parte (23)
7136
7136
7136
7136
7136
7136
Monter instalacji i urządzeń sanitarnych 7136
7136
więcej podobnych podstron