Wyznaczanie współczynnika lepkości cieczy za pomocą wiskozymetru Hoepplera .

(115)

OPIS TEORETYCZNY

W wielu przypadkach ciecze rzeczywiste zachowują się w przyblizeniu jak ciecz doskonała, tzn. nielepka i nieściśliwa. Dla cieczy nieściśliwej słuszne jest prawo ciągłości przepływu. Wynika z niego, że rurze ciecz osiąga największą prędkość w miejscach o małej powierzchni przekroju.
Z drugiej strony prędkość cieczy w rurze zależy od ciśnień: statycznego i hydrodynamicznego, o czym mówi równanie Bernoulliego.
Oba te prawa nie uwzględniają różnicy prędkości cząsteczek cieczy znajdujących się w różnej odległości od ścianek rury, gdyż nie uwzględniają tarcia między cząsteczkami cieczy, tzw. tarcia wewnętrznego.
Wskutek tarcia wystepującego między cząsteczkami cieczy, poruszająca się cząsteczka pociąga za sobą sąsiadujące cząsteczki tym silniej, im większa jest siła lepkości. Te cząsteczki pociągają następne itd... Każda następna warstwa porusza się jednak nieco wolniej, tym wolniej, im mniejsza lepkość cieczy. Prędkość spada do zera dla cząstek przy ściankach, które są jakby "przyklejone", a więc nieruchome.Tak więc maksymalną prędkość mają cząsteczki na osi rury, jak pokazuje to rysunek:

Taka sytuacja ma miejsce przy małych prędkościach cieczy przez gładką rurę. Mówimy, że przepływ jest laminarny, czyli warstwowy. Kolejne warstwy cieczy płyną nie zakłócając się wzajemnie.
Przy dużych prędkościach w cieczy popjawiają się zawirowania i ruch z laminarnego zmienia się w turbulentny. Rozkład prędkości jest wtedy nieco inny:

Do określenia lepkości cieczy posłużymy się takim modelem:

Płaską deseczkę leżąca na powierzchni cieczy w szerokim, płytkim naczyniu, ciągniemy siłą F, nadając jej stałą prędkość v₀. Warstwa cieczy przylegająca do deseczki ma prędkość taką samą jak deseczka, a kolejne, leżące coraz głębiej warstwy, mają prędkości coraz mniejsze. Warstwa cieczy przylegająca do dna jest nieruchoma. Zatem im płytsze naczynie, tym szybciej maleje wraz z głębokością prędkość cieczy.
Z doświadczenia wynika, że wielkość tych zmian powiązna jest z działającą siłą zależnością:

lub ogólniej

S to powierzchnia deseczki,

to takzwany gradient prędkości, czyli zmiana wartości prędkości weraz z głębokością x,

to współczynnik proporcjonalności pełniący tu rolę współczynnika lepkości dynamicznej
Korzystając z powyższego wzoru można wyprowadzić wzór, zwany prawem Poiseuille'a

Wzór ten podaje, jaka objętość cieczy o współczynniku lepkości
przepływa w czasie t przez rurę o promieniu  R i długości  l, przy różnicy ciśnień na końcach rury  p₁-p₂
Korzystając z tego wzoru, można określić wielkość siły tarcia na jakie napotyka ciecz płynąca w rurze z średnią pędkością cząsteczek v_śr w przypadku przepływu laminarnego. Siła ta hamuje prędkość przepływu cieczy.
Wzór ten ma postać:

Zlepkością cieczy wiąże się też zjawisko hamowania ruchu ciał poruszających się w lepkiej cieczy.
W przypadku gdy ciałem tym jest kulka, poruszająca się na tyle wolno, aby opływ cieczy był laminarny

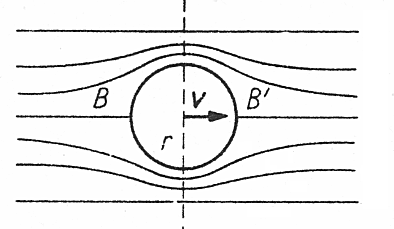
jak na tym rysunku
a nie turbulentny

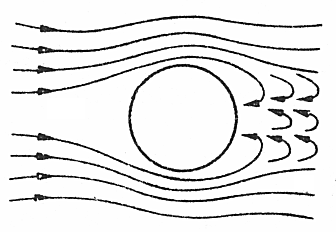
jak na tym rysunku
Siłę tę opisuje prawo Stokesa:

Korzystając z tego wzoru, można łatwo wyprowadzić wzór na prędkość kulki spadającej w lepkiej cieczy.

Wyznaczanie bezwzględnego współczynnika lepkości bezpośrednio z tego wzoru jest dość uciążliwe, ze względu na dużą liczbę występujących w nim wielkości. Aby nieco uprościć tę czynność skonstruowano przyrząd zwany wiskozymetrem Hoepplera. W wiskozymetrze tym stosuje się kulkę wykonaną z materiału o znanej gęstosci, której parametry (tzw stałą kulki K) określa się wstępnie w cieczy o znanej lepkości i gęstości. Teraz znając gęstość dowolnej innej cieczy, możemy wyznaczyć jej lepkość mierząc czas opadania kulki w tej cieczy na tym samym odcinku co w cieczy wzorcowej. W tym wypadku zamiast podanego wyżej wzoru korzystamy z wzoru uproszczonego:

We wzorze tym
to współczynnik lepkości badanej cieczy, t- czas opadania kulki w tej cieczy,
to gęstość kulki,
₁-gęstość cieczy, a K to właśnie stała kulki. Stałą aktualnie używanej kulki podano w instrukcji znajdującej się na stnowisku. Wyznacza się ją, mierząc czas opadania tej kulki w wiskozymetrze zawierającym ciecz o znanej lepkości i gęstosci.

CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie zależności współczynnika lepkości dynamicznej cieczy od temperatury w oparciu o badanie czasu opadania tej w cieczy kulki o znanych parametrach.

METODA POMIAROWA

Na rysunku poniżej widoczny jest przyrząd służący do pomiarów.

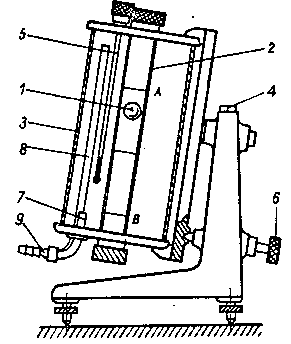
• 1- kulka opadająca w badanej cieczy

• 2- cylinder szklany z badaną cieczą

• 3- obudowa wypełniona wodą pełniącą rolę cieczy termostatującej

• 4- poziomica

• 5- termometr

• 6- zatrzask sprężynowy

• 7,8,9- podłączenia do termostatu

Wiskozymetr podłączony jest do wymuszonego obiegu wody, której temperatura stabilizowana jest przez ultratermostat z dokładnością do około 0,5 ^oC. Umopżliwia to wyznaczenie zależności współczynnika lepkości badanej cieczy od temperatury.
Rurka 2 wiskozymetru, w której opada kulka jest odchylona od pionu o ok. 10^o, aby zapobiec wahadłowemu opadaniu kulki, przez co opływ cieczy przestałby być laminarny.
Współczynnik lepkości wyznaczać będziemy z zależności:

W tym celu, po ustabilizowaniu się określonej tempetratury, zmierzymy kilkukrotnie czas opadania kulki pomiędzy określonymi poziomami (oznaczonymi na cylindrze kreskami A i B).
Pomiary powtarzamy w kilku temperaturach w zakresie od 25^oC do 60 ^oC.

OPRACOWANIE WYNIKÓW POMIARÓW

Dokładny przebieg pomiarów podany jest w instrukcji stanowiskowej (napisanej w WORD 2000), w której zamieszczona jest również tabelka. (Rozpakować bardzo wygodnie można ten plik np. przy pomocy Windows Commandera)

Proponowana tabelka ma postać:




W tabeli tej wpisujemy, wyrażone w kelwinach, temperatury, w których mierzymy czas opadania kulki oraz czasy opadania kulki. Pozostałe wielkości wpisujemy do tabelki na podstawie podanych w instrukcji stanowiskowej danych.
Gęstość cieczy w danej temperaturze wyliczamy według podanego w instrukcji wzoru:

Na podstawie tabelki należy sporzadzić dwa wykresy:
  oraz  

Pierwszy przedstawia po prostu przebieg zmian lepkości badanej cieczy w funkcji temperatury - powinien być fragmentem pewnej funkcji wykładniczej:

Dlatego punkty drugiego wykresu powinniśmy dopasować do prostej, najlepiej metodą regresji liniowej, aby na podstawie współczynnika kierunkowego (a) tej prostej wyznaczyć wartość energii aktywacji E

Z faktu, że ciecz jest praktycznie nieściśliwa wynika, że prędkość cieczy w miejscach o mniejszym przekroju jest większa, niż w miejscu o przekroju większym (gdy ciecz wypełnia całą rurę). Po prostu tyle samo cieczy musi przepłynąć przez dowolny przekrój. Opisuje to prawo ciągłości przepływu

,
które mówi, że w dowolnym miejscu rury iloczyn prędkości cieczy i pola powierzchni przekroju rury jest taki sam. Zatem w jednostce czasu, przez dowolny przekrój rury przepływa tyle samo cieczy.

Dla przepływu cieczy nieściśliwej ma zastosowanie równanie Bernoulliego które mówi, że dla dowolnego odcinka przewodu z cieczą, całkowite ciśnienie jest stałe. Ciśnienie to jest sumą ciśnienia statycznego p, ciśnienia hydrostatycznego
(h- to różnica wysokości słupa cieczy), oraz ciśnienia dynamicznego

(v- to prędkość cieczy).

Wskutek lepkości prędkość cieczy w całym przekroju rury nie jest stała, lecz zmienia się od zera (v=0) przy ściankach, do maksymalnej wartości w środku rury. Jeżeli przepływ jest laminarny, to rozkład prędkości ma symetrię osiową i zależy tylko od odległości r od osi rury. Aby określić prędkość przepływu cieczy w różnych miejscach i ilość cieczy przepływającej przez rurę w określonym czasie, rozważę ruch porcji wody w kształcie walca o długości l, płynącej w rurze o promieniu R.

Na powierzchnię boczną wybranego walca działa siła

Wskutek różnicy ciśnień na końcach walca na tę porcję cieczy działa siła P:

Skoro przepływ cieczy jest stacjonarny (prędkość cieczy nie zmienia się w czasie), wszystkie siły się równoważą , czyli siła P równa jest sile lepkości (P= -F):

Zatem

i

Całkując znajdujemy prędkość cieczy.

Stałą całkowania C wyznaczamy z warunku, że v(R)=0:

I tak otrzymujemy wzór na prędkość cieczy w zależności od odległości od osi rury:

Warto zauważyć, że z wzoru tego wynika, iż rozkład prędkości ma kształt paraboli:

W czasie t przez pierścień o promieniu r i szerokości dr przepływa ilość cieczy zajmująca objętość dV:

Przez całą rurę przepłynie w tym czasie:

Całkowanie daje nam ostecznie wynik

Równanie to nosi nazwę prawa Hagena-Poiseuille'a

Korzystając z prawa Hagena-Poiseuille'a można wyprowadzić średnią prędkość laminarnego przepływu cieczy w rurze:

W przypadku ruchu ustalonego (v_śr=0) siła P= S
p wynikająca z różnicy ciśnień
p równoważy siłę tarcia F.
Z powyższego wzoru na prędkość średnią otrzymamy zatem:

Tak więc ciecz płynąca w rurze o promieniu R i długości l, napotyka na siłę oporu związaną z lepkością cieczy równą:

Na kulę poruszającą się w lepkiej cieczy z prędkością v taką, aby ruch cieczy względem kuli był laminarny (jak na rysunku):

działa siła wyrażona wzorem Stokesa:

Rozważmy przypadek małej kulki o promieniu r spadającej w lepkiej cieczy. Na kulkę tę działają trzy siły: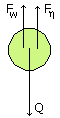



     Q- siła ciężkości;
    F_w- siła wyporu;
    
-siła lepkości
Siły te wyrazić można wzorami:






Na początku ruchu siła ciężkości jest większa od sumy pozostałych sił zgodnie z równaniem:

i kulka porusza się ruchem przyspieszonym (niejednostajnie).
Ponieważ jednak wraz ze wzrostem prędkości rośnie siła lepkości (dwie pozostałe siły są stałe), dochodzi wkrótce do momentu, gdy suma sił w powyższym równaniu staje się równa zeru:

Jak wiemy z I zasady dynamiki :

("jeżeli na ciało nie działa żadna siła, lub działające siły równoważą się, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym")

od tej chwili kulka będzie poruszać się ze stałą prędkością, którą wyznaczamy z powyższego równania:

Stąd wzór na prędkość kulki:

Z tego wzoru wynika, że małe kulki uzyskują mniejszą prędkość niż duże. Dlatego np. małe kropelki deszczu opadają w powietrzu dużo wolniej niż duże.
Wzór ten może posłużyć do wyznaczania lepkości cieczy lub gazu w oparciu o pomiar prędkości opadania kulki o znanym promieniu.

Funkcja wykładnicza:

opisuje przybliżoną zależność lepkości cieczy od temperatury. W wykładniku tego wyrażenia wystepuje tzw. energia aktywacji E. W uproszczeniu jej sens można wyjasnić w następujący sposób: wzajemne przemieszczanie się w cząstek w lepkiej cieczy nie zachodzi swobodnie lecz z pewnym utrudnieniem. Cząstka taka zanim się przemiesci w nowe położenie trwa przez jakiś czas w pewnym chwilowym położeniu równowagi, wykonując zwykłe drgania termiczne (podobnie jak w ciele stałym). Po pewnym czasie (tzw. czasie relaksacji) czastka przeskakuje w inne położenie itd. Aby jednak cząstka mogła zająć to inne położenie musi wytworzyć się (wskutek drgania innych cząstek) tzw. wnęka cząsteczkowa czyli miejsce dla tej cząsteczki. Energia potrzebna na wytworzenie takiej wnęki jest właśnie tą energią aktywacji. Jest ona zależna od ciśnienia cieczy i w pewnym stopniu od temperatury cieczy.

Pomiar prędkości grawitacyjnych fal wodnych(224)

OPIS TEORETYCZNY

Szczegółowy opis mechanicznych fal rozchodzących się w wodzie jest zagadnieniem dość złożonym, dlatego ograniczę się tylko do najprostszych fal. Zajmę się mianowicie sinusoidalnymi, poprzecznymi falami płaskimi na powierzchni wody. Jeśli dodatkowo pominie się siły lepkości wody, pozostaną do rozpatrzenia jedynie siła grawitacji i siła napięcia powierzchniowego. Pełnią one rolę sił sprężystych t.j. przywracających do położenia równowagi powierzchnię cieczy odchyloną od poziomu przez biegnacą falę. Dla fal dłuższych rolę dominującą mają siły grawitacji (tzw fale grawitacyjne), dla krótszych, siły napięcia powierzchniowego (tzw fale kapilarne).
Sposób rozchodzenia się tych fal zależy również od głebokości wody. Należy rozpatrzyć tu trzy przypadki :

• fale grawitacyjne ( "długie" ),

• fale kapilarne ( "krótkie"),

• fale grawitacyjno-kapilarne (pośredniej długości).

Analizując ruch cząsteczek wody biorących udział w przenoszeniu fali, dochodzimy do wniosku, że każda z nich porusza się po okręgu o pewnym promieniu "r" ( będącym równocześnie amplitudą fali) w płaszczyźnie pionowej .





Szczegółowe rachunki prowadzą do związku dyspersyjnego, który dla fal grawitacyjno-kapilarnych przyjmuje postać :



Na prędkość fazową fali otrzymamy zaś wzór :



W wyrażeniach tych pierwszy człon pod pierwiastkiem opisuje wpływ sił napiecia powierzchniowego, drugi zaś wpływ sił grawitacji. Dlatego dla fal, "czysto" grawitacyjnych możemy ograniczyć się tylko do postaci :



A dla fal "czysto" kapilarnych :



Z wzorów tych wynika, iż prędkość fali silnie zależy od jej długości. Dla fal grawitacyjnych rośnie wraz z długością, dla kapilarnych maleje. Obrazuje to wykres :




Z ogólnego związku dyspersyjnego łatwo znaleźć minimalną prędkość fali wodnej i odpowiadającą jej długość fali.



Dotychczasowe rozważania nie uwzględniały głebokości wody, w której rozchodzi się fala. Taki ogólny związek dyspersyjny ma postać
<BR.

Dla dużych głębokości tangens hiperboliczny th(kH) jest bliski jednosci, jednak dla płytkiej wody odgrywa już niepomijalną rolę. Możemy przyjąć wtedy, th(kH)=kH. Zatem


A dla fal "czysto" grawitacyjnych :


W naszym ćwiczeniu będziemy badać fale, które nie są czysto sinusoidalne, zmodyfikujemy więc nasz wzór do postaci następującej :

v=B^.g^1/2.h^A

gdzie v to prędkość, zaś A i B to stałe, przy czym B powinno wynosić okolo 1 natomiast A okolo 0,5 (tak jak we wzorze podstawowym , w ktorym v=(g^.h)^1/2 ).

CEL ĆWICZENIA

Celem ćwiczenia jest wyznaczenie zależności prędkości grawitacyjnych fal wodnych na płytkiej wodzie od głębokości zbiornika i porównanie jej z teoretyczną zależnością dla tych fal.

METODA POMIAROWA

Do pomiaru używamy prostopadłościennego naczynia o znanych wymiarach. Prędkość fali wyznaczamy z równania v=l/t, gdzie l jest długością zbiornika wody (lub jego wielokrotnością) a t czasem, w którym fala przebyła drogę l. Głębokość wody wyznaczamy z zależności h=V/S, gdzie V to objętość wlanej do naczynia wody, zaś S to powierzchnia naczynia. (W naszym przypadku l=1265 mm, a S=28,583 dm²)

PRZEBIEG POMIARÓW

1. Dokładnie wypoziomować naczynie

2. Wlać 3 litry zabarwionej wody

3. Unieść nieznacznie jeden z końców zbiornika (ok. 1 cm ) i szybko go opuścić

4. Gdy front powstałej fali przebiegnie dwie długości zbiornika (aby wytłumieniu uległy boczne fale) zmierzyć czas przebycia przez fale 2-3-krotnej długości naczynia.

5. Powtórzyć pomiar 5-krotnie

6. Dolewać po 1 litrze wody i powtarzać czynności z punktów 3-5 (10 różnych głębokości).

OPRACOWANIE WYNIKÓW POMIARÓW

Wyniki umieścić w tabeli pomiarowej :


Aby osiągnąć cel ćwiczenia należy znaleźć współczynniki A i B z równania

v=B^.g^1/2.h^A

W tym celu należy :

• Narysować wykres zależnosci log(v) od log(h)

• Metodą najmniejszych kwadratów wyznaczyć równanie prostej y=ax+b, najlepiej pasującej do wyników pomiarowych (w tym przypadku a=A, b=(1/2)^.log(g)+log(B), x=log(h), y=log(v) - sprawdzić, logarytmując wzór na v)

• Obliczyć odchylenia standardowe dla a i b

• Wyznaczyć A i B z równań A=a, B=10^b.(g^-1/2

• Obliczyć odchylenia standardowe dla A i dla B.

UWAGA
logarytmując rownanie na prędkość otrzymamy:
log(v) = log(B) + 1/2log(g) + A^.log(h)
Zatem wykres log(v) = f(log(h)) powinien być prostą i wyglądać mniej więcej tak jak na rysunku:

5.2. REGRESJA LINIOWA

Często spotykamy się z taką sytuacją, gdy mierzono dwie wielkości x i y związane są ze sobą równaniem liniowym

y = ax + b

tak jest np. w przypadku temperaturowej zależności oporu elektrycznego metali

R = f(T), skręcenia płaszczyzny polaryzacji światła w funkcji stężenia roztworu cukru a = f(s), okresu drgań relaksacyjnych w obwodzie kondensatora i neonówki od pojemności kondensatora T = f(C) itp.

Wykonując pomiary tych dwu wielkości x i y uzyskujemy pary liczb (x_i, y_i) i naszym zadaniem jest znaleźć równanie linii prostej (tzn. parametry a i b w równaniu prostej), najlepiej "pasującej" do nich. Niech równanie to będzie miało postać

a "dopasowanie" zgodnie z metodą najmniejszych kwadratów oznacza, że

gdzie a i b są emiprycznymi współczynnikami regresji liniowej.

Jak łatwo zauważyć, wyrażenie w nawiasie w tym równaniu jest odchyleniem punktu eksperymentalnego (liczonym wzdłuż osi y) od odpowiadającej mu wartości wynikającej z równania prostej. Poszukując ekstremum związanego powyższego równania udowadnia się, że

gdzie i = 1,2,3,...,n, czyli n jest ilością par punktów (x_i, y_i).

Na odchylenie standardowe S_a i S_b, będące miarą niepewności pomiarowych współczynników regresji a i b otrzymuje się następujące równania

 

Kryterium tego, jak nasze punkty pomiarowe (x_i,y_i) potwierdzają liniową zależność pomiędzy wielkościami x i y, stanowi wartość tzw. współczynnika korelacji liniowej r. Jego wartość zmienia się w granicach od
1 do 0. Gdy |r| = 1, to dopasowanie jest idealne, wszystkie punkty pomiarowe leżą na prostej. Gdy r = 0, to zależność liniowa pomiędzy x_i i y_i nie istnieje. W pomiarach fizycznych wartość współczynnika korelacji r jest zwykle większa niż 0,98. Wzór na współczynnik korelacji

Przykład 11. Wykonując pomiary temperaturowej zależności oporu elektrycznego

metalu otrzymano następujące rezultaty:

temperatura [^oC]	19	38	50	65	80
opór [ ]	150	159	170	175	185

Znaleźć równanie prostej najlepiej pasującej do tych danych oraz

współczynnik korelacji.

Wzory, z których będziemy korzystać ( zawierają różne sumy, które obliczymy na początku. U nas x_i to temperatury, a y_i to opory elektryczne, i = 1,2,3,4,5.

Podstawiając te wartości do wzorów (5.3) - (5.7) otrzymamy:

Tak więc nasze x i y spełniają równanie regresji liniowej postaci

y = 0,57 x + 139 lub y = 0,57(4) + 139(2)

Punkty pomiarowe i prosta o tym równaniu zostały pokazane na rysunku 5 , po lewej stronie.

5.3. TRANSFORMACJA NIEKTÓRYCH FUNKCJI NIELINIOWYCH

DO POSTACI LINIOWEJ

Regresję liniową można zastosować do tych zależności nieliniowych, które przez odpowiednią transformację zmiennych można zlinearyzować. Rozpatrzmy te, które spotyka się w pracowni studenckiej.

a) równanie typu

y = y_oe^ax

gdzie y_o i a są stałymi, które należy wyznaczyć.

Równanie tego typu opisuje np. zależność amplitudy drgań tłumionych od czasu

A = A_oe^-
t, aktywność próbki promieniotwórczej w czasie a = a_oe^-
t itp. Sprowadźmy to równanie do postaci liniowej. W tym celu najpierw zlogarytmujmy je stronami

ln y = ln y_o + ax

Jeżeli zatem na osi rzędnych odłożymy lny = z , to powyższe równanie będzie równaniem prostej

z = ln y_o + ax

gdzie b = ln y_o, zaś a= a

b) równanie typu

y = y_oe^a/x

Z równaniem tego typu spotykamy się, gdy badamy temperaturową zależność oporu elektrycznego półprzewodników R = R₀ e^-a/T, temperaturowa zależność współczynnika lepkości cieczy
=
_oe^E/RT, zależność temperatury wrzenia wody od ciśnienia p = p_oe^-E/RTitp. Aby sprowadzić takie równanie do postaci liniowej, należy je najpierw zlogarytmować

a następnie dokonać podstawienie

Wówczas otrzymamy

t = ln y_o + az,

które jest równaniem liniowym, wiążącym t i z.

Zatem sporządzając wykres, należy na osi odciętych odłożyć 1/x a na osi rzędnych ln y.

---