1. Wiadomości ogólne

Jeżeli wiązka światła przechodzi z jednego środowiska do drugiego, o innych własnościach optycznych, to na granicy dwóch ośrodków część promieniowania zostaje odbita, a część przechodzi do drugiego ośrodka ze zmianą kierunku promieni (załamanie). Zjawisko załamania jest opisane przez prawo:

1. Promień padający, promień załamany oraz normalna do powierzchni granicznej leżą w tej samej płaszczyźnie;

2. Stosunek sinusa kąta padania α do sinusa kąta załamania β jest dla dwu danych ośrodków wielkością stałą, która nosi nazwę względnego współczynnika załamania. Względny współczynnik załamania daje się wyrazić jako stosunek prędkości światła w obu ośrodkach:

Ponieważ prędkość rozchodzenia się fali w danym ośrodku (z wyjątkiem próżni) zależy od długości fali, zatem i współczynnik załamania zależeć będzie od długości fali. Zależność prędkości rozchodzenia się fal w danym ośrodku od ich długości nazywamy dyspersją ośrodka. Wynikająca z dyspersji zależność współczynnika załamania światłą n od długości fali λ ma na ogół postać złożoną. W zakresie długości fal, dla których pochłanianie światła jest niewielkie (ośrodek jest przezroczysty), zależność współczynnika załamania światła od długości fali może być opisana przybliżonym wzorem Cauchy'ego:

gdzie: A i B - stałe charakterystyczne dla danego ośrodka.

Jeżeli współczynnik załamania światła w ośrodku maleje ze wzrostem długości fali, to dyspersję nazywamy dyspersją normalną, natomiast jeżeli rośnie, to dyspersję nazywamy dyspersją anomalną.

Światło będące mieszaniną barw, przechodząc przez pryzmat, dzięki dyspersji ulega rozszczepieniu na poszczególne barwy, różniące się między sobą długością fali, a więc współczynnikiem załamania światła w ośrodku, z którego zbudowany jest pryzmat. Pozwala to na zbadanie zależności współczynnika załamania światła n w danym ośrodku od długości fali λ.

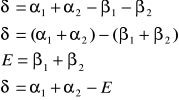
Po przejściu przez pryzmat o kącie łamiącym E, promień ulega odchyleniu od kierunku padania o kąt δ:

Wartość kąta odchylenia osiąga minimum gdy promień przechodzi przez pryzmat symetrycznie, tj. gdy w pryzmacie biegnie prostopadle do dwusiecznej kąta łamiącego. Wówczas, dla δ=δ_min, zachodzą relacje:

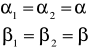
stąd:

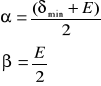
Podstawiając do wzoru na względny współczynnik załamania oraz przyjmując n₁=1 i n₂=n, możemy napisać:

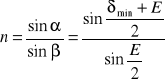
Mierząc kąt łamiący pryzmatu oraz kąt minimalnego odchylenia można wyznaczyć współczynnik załamania światła w substancji, z której wykonany jest pryzmat.

2. Pomiary

Wyznaczenie kąta łamiącego pryzmatu E:

Pomiar	Wartości kątów		Kąt łamiący E
I	ϕ1=250° 40'	ϕ2=140° 30'	59° 35'
II	ϕ1=254° 10'	ϕ2=134° 50'	59° 40'
III	ϕ1=255°	ϕ2=135° 40'	59° 40'
IV	ϕ1=267° 50'	ϕ2=148° 35'	59° 38'
V	ϕ1=273°	ϕ2=153° 45'	59° 38'

Kąt łamiący E obliczamy z następującego wzoru:

Obliczenia:

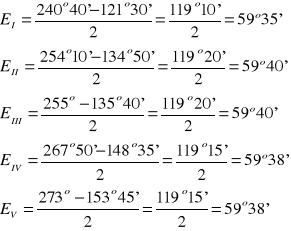
Ze średniej arytmetycznej:

E=59°38'

Wyznaczenie współczynnika załamania metodą minimalnego odchylenia:

Kąt początkowy położenia lunety:

ϕ₀=194° 25'

Prążek	Długość fali λ [μm]	Kąt ϕ	Kąt najmniejszego odchylenia dla prążków
fioletowy	0,45	ϕf=155° 15'	39°10'
niebieski	0,47	ϕn=155° 10'	39°15'
jasnoniebieski	0,50	ϕjn=155° 50'	38°35'
zielony	0,53	ϕz=156°	38°25'
żółty	0,59	ϕż=156° 5'	38°20'
pomarańczowy	0,61	ϕp=156° 10'	38°15'
czerwony	0,63	ϕc=156° 15'	38°10'

Kąt najmniejszego odchylenia obliczamy z następującego wzoru wzoru:

δ_min=ϕ_{0 -}ϕ

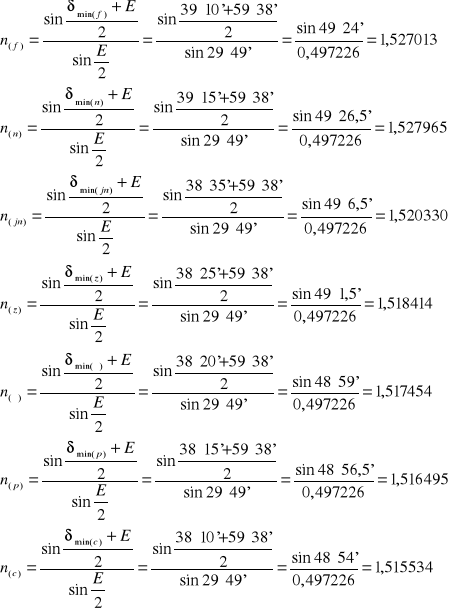
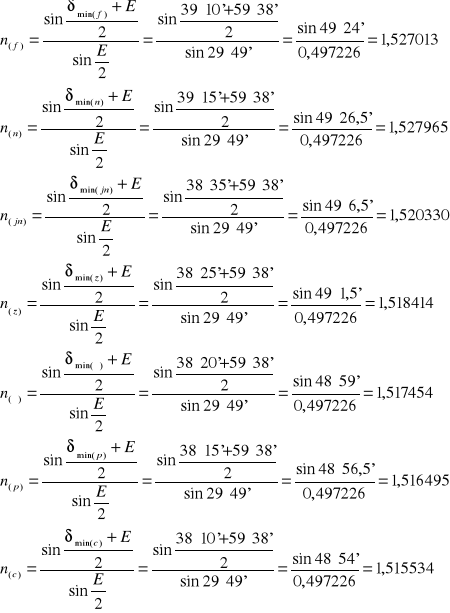
Obliczenia:

δ_min(f)= ϕ_0-ϕ_f=194° 25'-155° 15'=39°10'

δ_min(n)= ϕ_0-ϕ_n=194° 25'-155° 10'=39°15'

δ_min(jn)= ϕ_0-ϕ_jn=194° 25'-155° 50'=38°35'

δ_min(z)= ϕ_0-ϕ_z=194° 25'-156°=38°25'

δ_min(ż)= ϕ_0-ϕ_ż=194° 25'-156° 5'=38°20'

δ_min(p)= ϕ_0-ϕ_p=194° 25'-156° 10'=38°15'

δ_min(c)= ϕ_0-ϕ_c=194° 25'-156° 15'=38°10'

Współczynnik załamania w zależności od długości fali (λ)

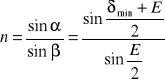
3. Ocena niepewności pomiarów:

Niepewność standardowa złożona U_c(E) pomiaru kąta łamiącego:

gdzie: ϕ₁, ϕ₂- niepewność standardowa w pomiarze kątów;

Niepewność pomiaru współczynnika załamania obliczamy metodą różniczki zupełnej jako bezwzględną, maksymalną niepewność złożoną:

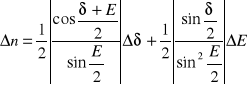
gdzie: ΔE≅U_C(E)

Niepewność pomiaru kąta odchylenia:

ΔE≅U_C(E)= 0,001028rad

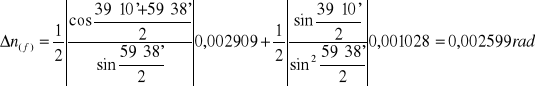
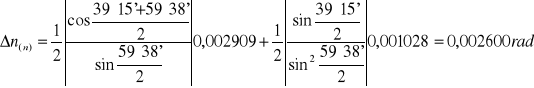
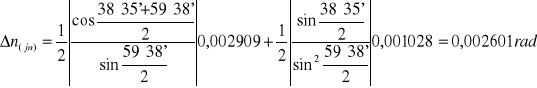
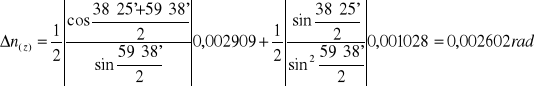
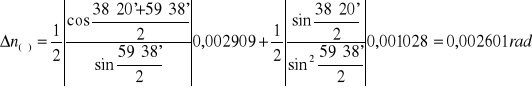
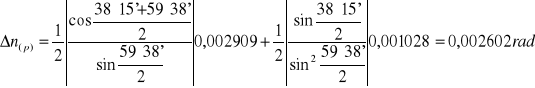
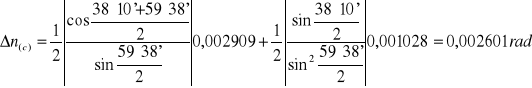
Niepewności pomiarów Δ(n²)=2n Δn:

Prążek	Współczynnik załamania w zależności od długości fali	Niepewności pomiarów Δ(n^2)	n^2	1/λ^2
fioletowy	1,527013	0,007937	2,331769	4,94
niebieski	1,527965	0,007945	2,334677	4,53
jasnoniebieski	1,520330	0,007908	2,311403	4,00
zielony	1,518414	0,007901	2,305581	3,56
żółty	1,517454	0,007893	2,302667	2,87
pomarańczowy	1,516495	0,007891	2,299757	2,69
czerwony	1,515534	0,007883	2,296843	2,52

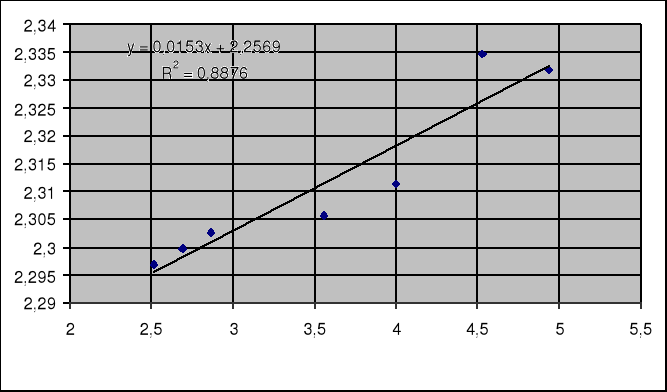
Ze wzoru Cauchy'ego:

n²=A+B/λ²

a=B i b=A

x=1/λ² i y=n²

y=ax+b

x_iy_i=

x_i=

y_i=

x_i²=

x_iy_i=58,1197

x_i=25,1049

y_i=16,1827

x_i²=95,3762

n=7

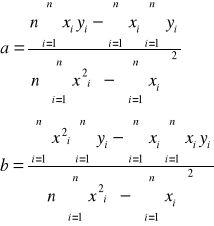
a=0,0153

b=2,2569

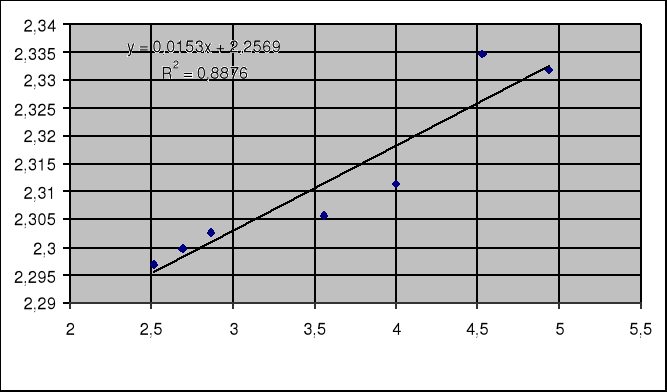
y=0,0153x + 2,2569

a zatem stałe charakterystyczne dla danego ośrodka są równe:

A=2,2569 i B=0,0153

Błędy i niepewności, które się pojawiły w wynikach mogą być spowodowane niedokładnością odczytu z urządzeń pomiarowych lub też ich niedokładnością spowodowaną np.: zużyciem tych urządzeń.

8

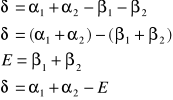
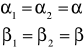
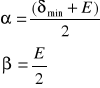
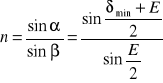
α₁

α₂

β₂

β₁

E

E

δ

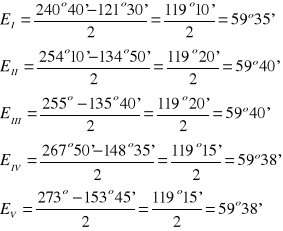
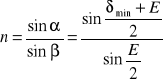
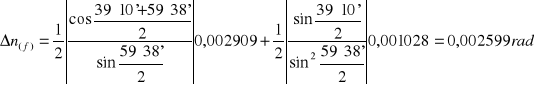
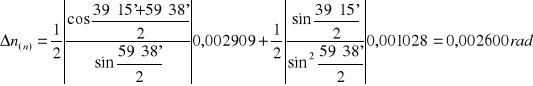
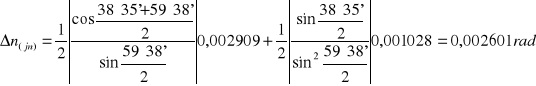
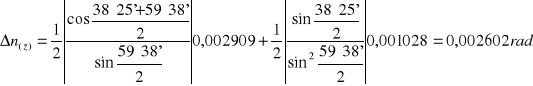
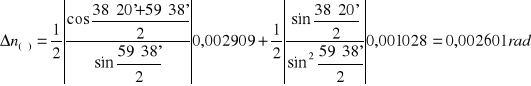
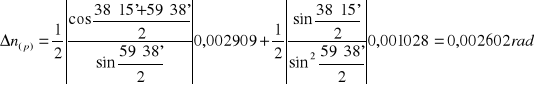
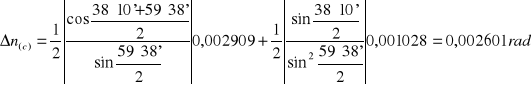
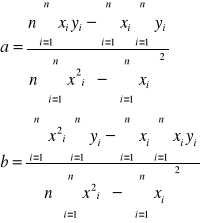
Lp.	n	λ
1	1,527013	0.45
2	1,527965	0.47
3	1,520330	0.50
4	1,518414	0.53
5	1,517454	0.59
6	1,516495	0.61
7	1,515534	0.63

---