Akademia Rolnicza w Krakowie Rok akademicki 1999/00

Wydział Inżynierii Środowiska i Geodezji Rok studiów III

Inżynieria Wodna Grupa 1b

Katedra Mechaniki Gruntów i Budownictwa Ziemnego

Projekt

stopy fundamentowej żelbetowej obciążonej słupem żelbetowym.

Projekt zawiera:

1. Ustalenie poziomu posadowienia. Schemat obliczeniowy.

2. Zestawienie normowych i obliczeniowych własności geotechnicznych podłoża.

3. Obliczenie oporu jednostkowego podłoża. Wyznaczenie boku stopy.

4. Zaprojektowanie wymiarów fundamentu.

5. Sprawdzenie warunku wg pierwszego stanu granicznego w poziomie posadowienia.

6. Sprawdzenie warunku wg drugiego stanu granicznego w stropie warstwy słabej.

7. Obliczenie naprężeń pierwotnych, wtórnych, dodatkowych i całkowitych.

8. Obliczenie spodziewanych osiadań. Sprawdzenie warunku wg drugiego stanu granicznego.

9. Obliczenie zbrojenia stopy.

10. Rysunek konstrukcyjny stopy. Wykres zaniku naprężeń.

Zając Stanisław

1.Ustalenie poziomu posadowienia. Schemat obliczeniowy.

1.1 Poziom posadowienia ustalamy ze względu na:

1. Głębokość przemarzania zasadniczo poniżej umownego 1.0 m

2. Głębokość zalegania wody gruntowej - poziom posadowienia powinien być powyżej zwierciadła wody gruntowej.

3. Względy konstrukcyjne - poziom posadowienia przyjmujemy nie głębiej niż 3.0 m i nie płycej niż 0.5 m.

4. Ze względu na układ warstw geotechnicznych powinien być albo bezpośrednio na stropie warstwy słabej , albo daleko od niej.

Jeżeli w podłożu występują warstwy gruntów spoistych i niespoistych to za warstwą mocniejszą będziemy uważać warstwy gruntu niespoistego. Na takich warstwach powinniśmy posadowić fundament.

5. Poziom posadowienia staramy się przyjmować na granicach warstw geotechnicznych.

Poziom posadowienia wg kryteriów 1 - 5 wynosi 1,10 m .

Dmin = 1,10 m

Dane z tematu:

Q_r=1700 [kN]

a×b=0,45×0,45 [m]

przyjęto poziom posadowienia równy 1,10 [m]

Schemat obliczeniowy.

2. Zestawienie normowych i obliczeniowych własności geotechnicznych podłoża.

Lp	Nazwa gruntu	ρs^n t/m­^3	W^n %	ρ^n t/m­^3	ρd t/m­^3	n	ρ^r=0,9*ρ^n t/m­^3	ρ^r=1,1*ρ^n t/m­^3	ρ^nsr t/m­^3	ρ'^n t/m­^3	ρ^rsr=0,9*ρ^nsr t/m­^3	ρ^rsr=1,1*ρ^nsr t/m­^3	ρ'^r=0,9*ρ'^n t/m­^3	ρ'^r=1,1*ρ'^n t/m­^3
1	Πp IL=0,08	2,66	18	2,10	1,78	0,33	1,89	2,31	-	-	-	-	-	-
2	PΠ ID=0,36	2,65	16	1,75	1,51	0,43	1,58	1,93	-	-	-	-	-	-
3	Pg IL=0,18	2,65	13	2,15	1,90	0,28	1,94	2,37	2,18	-	1,97	2,40	-	-
4	Pg IL=0,18	2,65	13	2,15	1,90	0,28	1,94	2,37	2,18	1,18	-	-	1,07	1,30
5	Gp IL=0,13	2,67	12	2,20	1,96	0,26	1,98	2,42	2,23	1,23	-	-	1,11	1,35
6	Pr ID=0,40	2,65	22	2,00	1,64	0,38	1,80	2,20	2,02	1,02	-	-	0,92	1,12

Obliczenia dla P_Π:

-gęstość objętościowa szkieletu -gęstość objętościowa gruntu uwodnionego powyżej zwierciadła wody gruntowej

ρ_srⁿ=(1-n)⋅ρ_s+n⋅ρ_w [t/m³] ρ_srⁿ=(1-0,43) ⋅2,65+0,43⋅1=1,94 [t/m³]

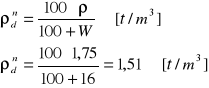
-porowatość -gęstość objętościowa gruntu uwodnionego poniżej zwierciadła wody gruntowej

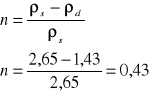
ρ'ⁿ=ρ_sr-1 [t/m³] ρ'ⁿ=1,94-1=0,94 [t/m³]

3. Obliczenie oporu jednostkowego podłoża. Wyznaczenie boku stopy.

Opór jednostkowy:

B - szerokość boku stopy [m]

L - długość boku stopy [m]

ρ^r_D - średnia obliczeniowa gęstość gruntu zalegającego bezpośrednio powyżej poziomu posadowienia [t/m³]

ρ^r_B - średnia obliczeniowa gęstość gruntu zalegającego bezpośrednio poniżej poziomu posadowienia [t/m³]

C^r_u - obliczeniowa wartość spójności gruntu zalegającego bezpośrednio poniżej poziomu posadowienia [kPa]

∅^r_u - obliczeniowa wartość kąta tarcia wewnętrznego gruntu zalegającego bezpośrednio poniżej poziomu posadowienia [ kPa]

N_C, N_D, N_B - współczynniki nośności wyznaczone w oparciu o ∅^ru

D_min. - poziom posadowienia [m]

g - przyśpieszenie ziemskie; g = 9,81 [m/s²].

Pierwsze przybliżenie

B = L = 1,0 [m]

γ_m = 0,9

ρ^r_D=1,80 [t/m³]

ρ^r_B=1,58 [t/m³]

Określenie kąta tarcia wewnętrznego i kohezji:

P_Π I_D = 0,36

Cⁿ_u = 0 [kPa]

∅ⁿ_u = 29,8 [^Ο]

C^r_u = Cⁿ_u ⋅0,9 = 0⋅0,9 = 0 [kPa]

∅^r_u = ∅ⁿ_u⋅0,9 = 29,8⋅0,9 = 26,82 [^Ο]

Współczynniki nośności:

N_C = 23,64

N_D = 12,96

N_B = 4,54

Opór jednostkowy:

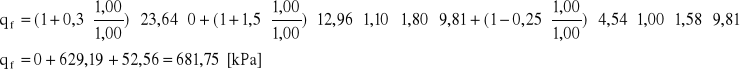
q_f = 681,75 [kPa]

Warunek wg pierwszego stanu granicznego

q_rs ≤ m⋅q_f

q_rs -całkowite naprężenia działające w poziomie posadowienia

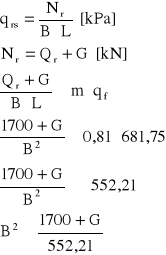
naprężenia pierwotne

δ_g = h⋅g⋅ρ [kPa]

h = D_min = 1,10 [m]

δ_g = D_min ⋅g⋅ρ

ρ_żelbetu = 2,40 [t/m³]

δ_g = 1,10⋅2,40⋅9,81 = 25,90 [kPa]

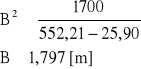
przyjmuję B = 1,80 m

4. Zaprojektowanie wymiarów fundamentu.

a. Wysokość ekonomiczna stopy

- metoda przybliżona

h = χ⋅ (B - a_s) [m]

B = 1,80 [m] - szerokość boku stopy

a_s = 0,45 [m] - szerokość boku słupa

χ = 0,45 - współczynnik zależny od naprężeń pod stopą dla q_rs= 526,32 [kPa]

h = 0,45⋅(1,80 - 0,45) = 0,61 [m]

przyjęto h = 0,65 [m]

χ = 0,45 - współczynnik zależny od naprężeń pod stopą

h = 0,45⋅(1,90 - 0,45) = 0,65]

przyjęto h = 0,65 [m]

-metoda w oparciu o wysokość efektywną stopy

h = h₁+ (0,05÷0,07) [m]

a_sb

B

h₁ h

dane: B = L = 1,80 [m]

a_s = 0,45 [m]

Q_r = 1700 [kPa]

dla betonu B10 R_b = 580 [kPa]

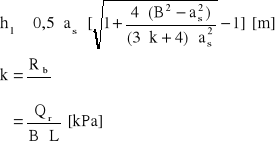
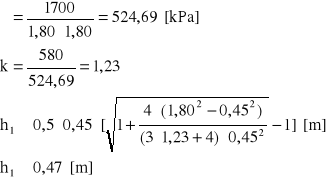
h = 0,47 + 0,06 = 0,53 [m]

przyjęto h=0,55 [m]

dla betonu B15 R_b=750 [kPa]

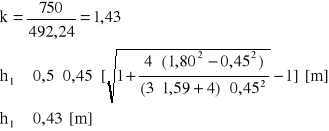
h = 0,43 + 0,06 = 0,49 [m]

przyjęto h = 0,50 [m]

Ostatecznie przyjęto do dalszych obliczeń przyjęto h = 0,55 [m]

0,55

B

5. Sprawdzenie warunku wg. pierwszego stanu granicznego w poziomie posadowienia

Warunek wg pierwszego stanu granicznego

q_rs ≤ m⋅q_f

q_rs -całkowite naprężenia działające w poziomie posadowienia

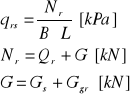
G_s-ciężar stopy

G_gr-ciężar gruntu

Objętość stopy

F = B⋅L = 1,80⋅1,80 = 3,24 [m²]

a_s = 0,45 0,55

Dmin = 1,10

0,40

b = 0,55 h = 0,55

0,15

B =1,80

b = 0,55

V_s = 1,09 [m³]

G_s = V_s⋅ρ_żelb⋅g = 1,09⋅2,40⋅9,81 = 25,67 [kN]

V_gr = D_min⋅B²-V_s-( D_min-h) ⋅a_s [m³]

V_gr = 1,10⋅1,80² - 1,09 - (1,10 - 0,55) ⋅0,45 = 2,23 [m³]

G_gr = V_gr⋅ρ_gr ⋅g = 2,23⋅2,21⋅9,81 = 48,18 [kN]

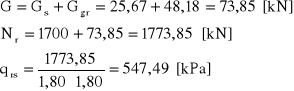
B = L = 1,80 [m]

D_min=1,10 [m]

ρ^I_D=1,80 [t/m³]

ρ^I_B = 1,58 [t/m³]

P_Π

C^I_u = 0 [kPa] ∅^r_u = 26,82 [^Ο] N_C = 23,64 N_D = 12,96 N_B = 4,54

Opór jednostkowy:

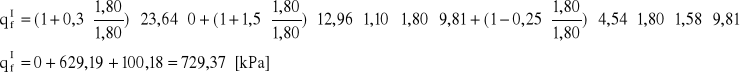
Sprawdzenie warunku

q_rs ≤ m⋅q_f

547,49 < 0,81⋅729,37

547,49 < 590,79 [kPa]

Pierwszy stan równowagi granicznej w poziomie posadowienia został zachowany.

6. Sprawdzenie warunku wg drugiego stanu granicznego w stropie

warstwy słabej.

Schemat obliczeniowy.

h = 1.90 [m] > B = 1,80 [m] → b =

B' = L' = 1,80+0,63=2,43 [m]

N'_r= N_r+ B'⋅L'⋅ρ_h^r⋅g = 1773,85 + 2,43⋅2,43⋅1,93⋅9,81=1885,65 [kN]

q'_rs ≤ m⋅q'_f

D'_min.= 3,00 [m]

B' = L' = 2,43 [m]

γ_m = 0,9

ρ'^r_B=1,30 [t/m³]

Określenie kąta tarcia wewnętrznego i kohezji:

P_g I_L:=0,18

C'ⁿ_u =17 [kPa]

∅'ⁿ_u=15 [^Ο]

C'^r_u = C'ⁿ_u *0,9=17*0,9=15,30 [kPa]

∅'^r_u=∅'ⁿ_u*0,9=15*0,9=13,50 [^Ο]

Współczynniki nośności:

N ^′_C = 10,68

N ′_D = 3,77

N ′_B = 0,54

Opór jednostkowy:

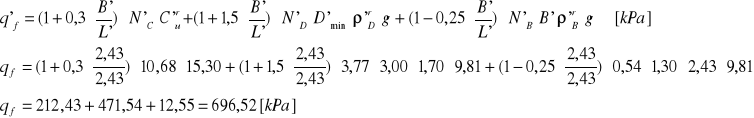
q'_rs ≤ m⋅q'_f

q'_rs = 319,30 [kPa] < m⋅q'_f = 0,81⋅696,52 = 564,19 [kPa]

Pierwszy stan równowagi granicznej w stropie warstwy słabej został zachowany.

7. Obliczenie naprężeń pierwotnych, wtórnych, dodatkowych i całkowitych.

Naprężenia pierwotne:

Schemat obliczeniowy.

Naprężenia pierwotne:

σ_zρ=Σh⋅ρ⋅g [kPa]

σ_zρ0,80 = 0,80⋅2,10⋅9,81 = 16,48 [kPa]

σ_zρ1,10 = 16,48 + 0,30⋅1,75⋅9,81 = 21,63 [kPa]

σ_zρ1,80 = 21,63 + 0,70⋅1,75⋅9,81 = 33,65 [kPa]

σ_zρ2,40 = 33,65 + 0,60⋅1,75⋅9,81 = 43,95 [kPa]

σ_zρ3,00 = 43,95 + 0,60⋅1,75⋅9,81 = 54,25 [kPa]

σ_zρ3,50 = 54,25 + 0,50⋅2,18⋅9,81 = 64,94 [kPa]

σ_zρ4,50 = 64,94 + 1,00⋅1,18⋅9,81 = 76,52 [kPa]

σ_zρ5,50 = 76,52 + 1,00⋅1,18⋅9,81 = 88,09 [kPa]

σ_zρ6,75 = 88,09 + 1,25⋅1,23⋅9,81 = 103,17 [kPa]

σ_zρ8,00 = 103,17 + 1,25⋅1,23⋅9,81 = 118,25 [kPa]

Naprężenia wtórne:

σ_zs = σ_os⋅η_s [kPa]

η_s- współczynnik zaniku naprężeń

σ_os = σ_oρ= σ_zρ1,10 = 24,71 [kPa]

h = 1,10 [m] z = 0 ; z/B = 0 η_s = 1,00 σ_zs1,10 = 21,63 ⋅ 1,00 = 21,63 [kPa]

h = 1,45 [m] z = 0,35 ; z/B = 0,19 η_s = 0,77 σ_zs1,45 = 21,63 ⋅ 0,77 = 16,66 [kPa]

h = 2,10 [m] z = 1,00 ; z/B = 0,56 η_s = 0,50 σ_zs2,10 = 21,63 ⋅ 0,50 = 10,82 [kPa]

h = 2,70 [m] z = 1,80 ; z/B = 1,00 η_s = 0,28 σ_zs2,70 = 21,63 ⋅ 0,28 = 6,06 [kPa]

h = 3,25 [m] z = 2,15 ; z/B = 1,19 η_s = 0,23 σ_zs3,25 = 21,63 ⋅ 0,23 = 4,97 [kPa]

h = 4,00 [m] z = 2,90 ; z/B = 1,61 η_s = 0,15 σ_zs4,00 = 21,63 ⋅ 0,15 = 3,24 [kPa]

h = 5,00 [m] z = 3,90 ; z/B = 2,17 η_s = 0,08 σ_zs5,00 = 21,63 ⋅ 0,08 = 1,73 [kPa]

h = 6,12 [m] z = 5,02 ; z/B = 2,79 η_s = 0,06 σ_zs6,12 = 21,63 ⋅ 0,06 = 1,29 [kPa]

h = 7,38 [m] z = 6,28 ; z/B = 3,49 η_s = 0,05 σ_zs7,38 = 21,63 ⋅ 0,05 = 1,08 [kPa]

Naprężenia dodatkowe:

σ_zd = η_s⋅ (q_rs-σ_oρ) [kPa]

q_rs = 547,49 [kPa]

σ_oρ = σ_zρ1,10 = 21,63 [kPa]

σ_zd = η_s⋅ (547,49-21,63) = η_s ⋅ 525,86 [kPa]

σ_zd1,10 = 1,00 ⋅ 525,86 = 525,86 [kPa]

σ_zd1,45 = 0,77 ⋅ 525,86 = 404,91 [kPa]

σ_zd2,10 = 0,50 ⋅ 525,86 = 262,93 [kPa]

σ_zd2,70 = 0,28 ⋅ 525,86 = 147,24 [kPa]

σ_zd3,25 = 0,23 ⋅ 525,86 = 120,95 [kPa]

σ_zd4,00 = 0,15 ⋅ 525,86 = 78,88 [kPa]

σ_zd5,00 = 0,08 ⋅ 525,86 = 47,32 [kPa]

σ_zd6,12 = 0,06 ⋅ 525,86 = 31,55 [kPa]

σ_zd7,38 = 0,05 ⋅ 525,86 = 26,29 [kPa]

Naprężenia wtórne na granicach warstw geotechnicznych:

h = 3,00 [m] z = 1,90 ; z/B = 1,06 η_s = 0,26 σ_zs3,00 = 21,63 ⋅ 0,26 = 5,62 [kPa]

h = 3,50 [m] z = 2,40 ; z/B = 1,33 η_s = 0,18 σ_zs3,00 = 21,63 ⋅ 0,18 = 3,89 [kPa]

h = 5,50 [m] z = 4,40 ; z/B = 2,44 η_s = 0,08 σ_zs5,50 = 21,63 ⋅ 0,08 = 1,73 [kPa]

h = 8,00 [m] z = 6,90 ; z/B = 3,83 η_s = 0,04 σ_zs8,00 = 21,63 ⋅ 0,04 = 0,87 [kPa]

Naprężenia dodatkowe na granicach warstw geotechnicznych:

σ_zd3,00 = 0,26 ⋅ 525,86 = 136,72 [kPa]

σ_zd3,50 = 0,18 ⋅ 525,86 = 94,65 [kPa]

σ_zd5,50 = 0,08 ⋅ 525,86 = 42,07 [kPa]

σ_zd8,00 = 0,04 ⋅ 525,86 = 21,03 [kPa]

Sprawdzenie warunku σ_zd ≤ 0,3⋅σ_zρ

h = 5,50 [m] warstwa Pg

σ_zs5,50 = 42,07 [kPa] 0,3⋅σ_zρ = 0,3⋅88,09 = 26,42 [kPa]

Warunek nie został spełniony-do głębokości 5,50 m liczymy osiadania-sprawdzamy drugi stan graniczny.

h = 8,00 [m] warstwa G_p

σ_zs8,00 = 21,03 [kPa] 0,3⋅σ_zρ = 0,3⋅118,25 = 35,48 [kPa]

Warunek został spełniony-do głębokości 8,00 m liczymy osiadania-sprawdzamy drugi stan graniczny.

Naprężenia całkowite:

σ_zt=σ_zρ+σ_zd [kPa]

σ_zt1,10=21,63 + 525,86 = 547,49 [kPa]

σ_zt3,00=54,25 + 136,72 = 190,97 [kPa]

σ_zt3,50=64,94 + 94,65 = 159,59 [kPa]

σ_zt5,50=88,09 + 42,07 = 130,16 [kPa]

σ_zt8,00=118,25 + 21,03 = 139,28 [kPa]

8. Obliczenie spodziewanych osiadań. Sprawdzenie warunku wg drugiego stanu granicznego.

Osiadanie :

s = s'+s”

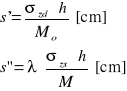
gdy λ = 0 to

gdzie:

h - miąższość warstewek [cm]

M_o - moduł ściśliwości pierwotnej [kPa]

M - moduł ściśliwości wtórnej [kPa]

λ - współczynnik zależny od czasu wznoszenia budowli (równy 0 lub1)

Lp	Rodzaj gruntu	Miąższość warstwy h [cm]	Zagłębienie środka warstwy [m]	σzd [kPa]	Mo [kPa]	s [cm]
1	G ID=0,36	70	1,45	404,91	47000	0,603
2	P ID=0,36	60	2,1	262,93	47000	0,336
3	P ID=0,36	60	2,7	147,24	47000	0,188
4	Pg IL=0,18	50	3,25	120,95	31000	0,195
5	Pg IL=0,18	100	4	78,88	31000	0,254
6	Pg IL=0,18	100	5	42,07	31000	0,136
7	Gp IL=0,13	125	6,12	31,55	28000	0,141
8	Gp IL=0,13	125	7,38	26,29	28000	0,117
					Razem	1,970

Sprawdzenie drugiego stanu granicznego:

s≤s_dop s_dop= 5,00 [cm]

s = 1,970 [cm] < s_dop = 5,00 [cm].

Warunek drugiego stanu granicznego jest spełniony.

9. Obliczenie zbrojenia stopy.

Schemat obliczeniowy:

Metoda Labell'a.

Sprawdzenie warunku stosowalności metody:

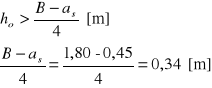
h₁= h-0,06 [m]

h₁= 0,55 - 0,06 = 0,49 [m]

Warunek jest spełniony - możemy stosować tę metodę.

Siła rozciągająca - Z

Zapotrzebowanie na powierzchnię zbrojenia

stosujemy stal okrągłą, gładką klasy A-I

STAL - St 3Sx → R_a=210 [MPa]

F ≥ 27,8 [cm²]

Przyjęto zbrojenie:

15 ∅16

F_a = 15⋅2,011 = 30,16 [cm²]

Rozstawa zbrojenia

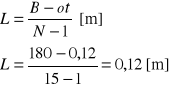
sprawdzenie warunku

10 [cm] ≤ L≤ ¼ ⋅h₁

10 [cm] = 12 [cm] ≤ ¼ ⋅h₁=12,25 [cm]

Warunek jest spełniony - rozstawa została zaprojektowana prawidłowo.

Zbrojenie słupa.

d-średnica zbrojenia

d = 26mm e' = 26 cm 10d = 26 cm

e = 35 cm < 40 cm

Warunki są spełnione.

Zestawienie ilości stali zbrojonej

Numer zbrojenia	d [mm]	Długość wkładek [cm]	Jlość wkładek [szt]	Długość zbrojenia [m]	Ciężar [kG/mb]	Ciężar ogółem [kG/mb]
1	16	1,68	15	25,2	1,578	39,7656
2	16	1,68	15	25,2	1,578	39,7656
					Suma	79,5312

Akademia Rolnicza w Krakowie Rok akademicki 1999/00

Wydział Inżynierii Środowiska i Geodezji Rok studiów III

Inżynieria Wodna Grupa 1b

Katedra Mechaniki Gruntów i Budownictwa Ziemnego

Projekt z fundamentowania

Temat: Projekt stopy fundamentowej żelbetowej obciążonej słupem żelbetowym.

Zając Stanisław

Π_p

I_L=0,08

P_Π

I_D=0,36

P_g

I_L=0,18

G_p

I_L=0,13

P_r

I_D=0,40

3,50

0,80

3,00

5,50

8,00

12,00

0,625 m 0,05 0,45 0,05 0,625 m

B=1.80 [m]

h=2⋅B= 3.60 [m]

D_min=1,10 [m] ρ^r_D=1.80 [t/m³]

z=B=1.80 [m] ρ^r_B= 1.58 [t/m³]

0,55 m

0,40 m

0,55 m

w=0,15 m

D_min.=1,10 m

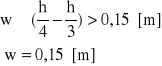
h

B = 1,80[m]

D_min=1,10 [m] ρ^r_D=1,80 [t/m³]

z=B=1,80 [m] ρ^r_B= 1,58 [t/m³]

0,80

3,00

5,50

8,00

12,00

Π_p

I_L=0,08

P_Π

I_D=0,36

P_g

I_L=0,18

G_p

I_L=0,13

P_r

I_D=0,40

0,80

3,00

5,50

8,00

12,00

Π_p

I_L=0,08

P_Π

I_D=0,36

P_g

I_L=0,18

G_p

I_L=0,13

P_r

I_D=0,40

3,50

D'_min=2,80 [m] ρ'^r_D=1,70 [t/m³]

ρ'^r_B= 1,30 [t/m³]

B=1,80 [m]

h=1,30 [m]

B'=2,43 [m]

z=2B=3,60 [m]

1,10

1,45

1,80

2,10

2,40

2,70

3,00

3,25

4,00

4,50

5,00

5,50

6,12

6,75

7,38

8,00

∏_p

I_L=0,08

P_∏

I_D=0,36

Pg

I_L=0,18

G_p

I_L=0,13

Pr

I_D=0,40

0,80

3,00

3,50

5,50

8,00

12,00

ρ^r=2,10 [t/m³]

ρ^r= 1,75 [t/m³]

ρ^r=2,18 [t/m³]

ρ^r=1,18 [t/m³]

ρ^r=1,23 [t/m³]

ρ^r=1,02 [t/m³]

B=1,80 [m]

z h

6 cm

h₁ h_o

Q_r=1700kN

B=1,80 m

a_sb

L

5-7cm

(otulina)

D_min=1,10 [m]

B=1.80 [m]

]

0,00

G

G

3,50

---