Akademia Rolnicza w Krakowie Rok akademicki 1998/99

Wydział Inżynierii Środowiska i Geodezji Rok studiów III

Inżynieria Wodna Grupa 2a

Katedra Mechaniki Gruntów i Budownictwa Ziemnego

Projekt

stopy fundamentowej żelbetowej obciążonej słupem żelbetowym.

Projekt zawiera:

1. Ustalenie poziomu posadowienia. Schemat obliczeniowy.

2. Zestawienie normowych i obliczeniowych własności geotechnicznych podłoża.

3. Obliczenie oporu jednostkowego podłoża. Wyznaczenie boku stopy.

4. Zaprojektowanie wymiarów fundamentu.

5. Sprawdzenie warunku wg pierwszego stanu granicznego w poziomie posadowienia.

6. Sprawdzenie warunku wg drugiego stanu granicznego w stropie warstwy słabej.

7. Obliczenie naprężeń pierwotnych, wtórnych, dodatkowych i całkowitych.

8. Obliczenie spodziewanych osiadań. Sprawdzenie warunku wg drugiego stanu granicznego.

9. Obliczenie zbrojenia stopy.

10. Rysunek konstrukcyjny stopy. Wykres zaniku naprężeń.

Bogusław Paśko

1. Ustalenie poziomu posadowienia. Schemat obliczeniowy.

Dane z tematu:

Q_r=1800 [kN]

a×b=0,50×0,50 [m]

przyjęto poziom posadowienia równy 1,20 [m]

Schemat obliczeniowy.

2. Zestawienie normowych i obliczeniowych własności geotechnicznych podłoża.

Lp	Nazwa gruntu	ρs^n t/m­^3	W^n %	ρ^n t/m­^3	ρd t/m­^3	n	ρ^r=0,9*ρ^n t/m­^3	ρ^r=1,1*ρ^n t/m­^3	ρ^nsr t/m­^3	ρ'^n t/m­^3	ρ^rsr=0,9*ρ^nsr t/m­^3	ρ^rsr=1,1*ρ^nsr t/m­^3	ρ'^r=0,9*ρ'^n t/m­^3	ρ'^r=1,1*ρ'^n t/m­^3
1	Gp IL=0,08	2,67	12	2,20	1,96	0,27	2,42	2,42	-	-	-	-	-	-
2	Pd ID=0,33	2,65	19	1,70	1,43	0,46	1,53	1,87	-	-	-	-	-	-
3	Gp IL=0,26	2,67	17	2,10	1,79	0,33	1,89	2,31	2,12	-	1,91	1,01	-	-
4	Gp IL=0,26	2,67	17	2,10	1,79	0,33	1,89	2,31	2,12	1,12	-	-	1,01	1,23
5	Gz IL=0,17	2,69	18	2,10	1,78	0,34	1,89	2,31	2,12	1,12	-	-	1,01	1,23
6	Ip ID=0,14	2,70	18	2,10	1,78	0,34	1,89	2,31	2,12	1,12	-	-	1,01	1,23

Obliczenia dla P_d :

-gęstość objętościowa szkieletu -gęstość objętościowa gruntu uwodnionego powyżej zwierciadła wody gruntowej

ρ_srⁿ=(1-n)⋅ρ_s+n⋅ρ_w [t/m³] ρ_srⁿ=(1-0,46) ⋅2,65+0,46⋅1=1,89 [t/m³]

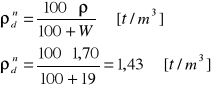
-porowatość -gęstość objętościowa gruntu uwodnionego poniżej zwierciadła wody gruntowej

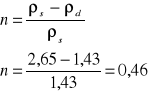
ρ'ⁿ=ρ_sr-1 [t/m³] ρ'ⁿ=1,89-1=0,89 [t/m³]

3. Obliczenie oporu jednostkowego podłoża. Wyznaczenie boku stopy.

Opór jednostkowy:

B - szerokość boku stopy [m]

L - długość boku stopy [m]

ρ^r_D - średnia obliczeniowa gęstość gruntu zalegającego bezpośrednio powyżej poziomu posadowienia [t/m³]

ρ^r_B - średnia obliczeniowa gęstość gruntu zalegającego bezpośrednio poniżej poziomu posadowienia [t/m³]

C^r_u - obliczeniowa wartość spójności gruntu zalegającego bezpośrednio poniżej poziomu posadowienia [kPa]

∅^r_u - obliczeniowa wartość kąta tarcia wewnętrznego gruntu zalegającego bezpośrednio poniżej poziomu posadowienia [ kPa]

N_C, N_D, N_B - współczynniki nośności wyznaczone w oparciu o ∅^ru

D_min. - poziom posadowienia [m]

g - przyśpieszenie ziemskie; g = 9,81 [m/s²].

Pierwsze przybliżenie

B = L = 1 [m]

γ_m = 0,9

ρ^r_D=1,72 [t/m³]

ρ^r_B=1,53 [t/m³]

Określenie kąta tarcia wewnętrznego i kohezji:

P_d I_D = 0,33

Cⁿ_u = 0 [kPa]

∅ⁿ_u = 29,8 [^Ο]

C^r_u = Cⁿ_u ⋅0,9 = 0⋅0,9 = 0 [kPa]

∅^r_u = ∅ⁿ_u⋅0,9 = 29,8⋅0,9 = 26,82 [^Ο]

Współczynniki nośności:

N_C=23,64

N_D=12,96

N_B=4,54

Opór jednostkowy:

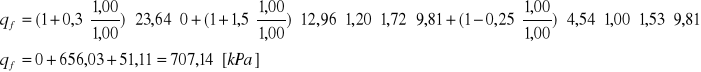
Warunek wg pierwszego stanu granicznego

q_rs ≤ m⋅q_f

q_rs -całkowite naprężenia działające w poziomie posadowienia

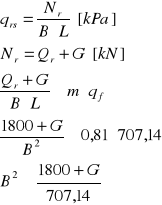
naprężenia pierwotne

δ_g = h⋅g⋅ρ [kPa]

h = D_min = 1,20 [m]

δ_g = D_min ⋅g⋅ρ

ρ_żelbetu = 2,40 [t/m³]

δ_g = 1,20⋅2,40⋅9,81 = 28,25 [kPa]

przyjmuję B = 1,90 m

4. Zaprojektowanie wymiarów fundamentu.

a. Wysokość ekonomiczna stopy

- metoda przybliżona

h=χ⋅ (B-a_s) [m]

B = 1,90 [m] - szerokość boku stopy

a_s = 0,50 [m] - szerokość boku słupa

χ = 0,45 - współczynnik zależny od naprężeń pod stopą dla q_rs= 572,78 [kPa]

h=0,45⋅(1,9 0-0,60) = 0,63 [m]

przyjęto h = 0,65 [m]

-metoda w oparciu o wysokość efektywną stopy

h = h₁+(0,05÷0,07) [m]

a_sb

B

dane: B = L = 1,90 [m]

a_s=0,50 [m]

Q_r=1800 [kPa]

dla betonu B10 R_b=580 [kPa]

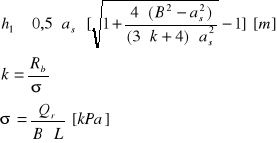
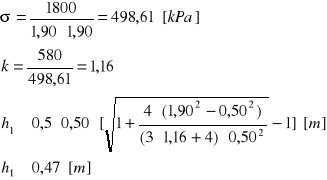
h=0,47+0,07=0,54 [m]

przyjęto h=0,55 [m]

dla betonu B15 R_b=750 [kPa]

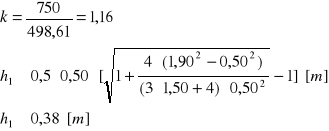
h=0,38+0,07=0,45 [m]

przyjęto h=0,45 [m]

Ostatecznie przyjęto do dalszych obliczeń przyjęto h=0,65 [m]

5. Sprawdzenie warunku wg pierwszego stanu granicznego w poziomie posadowienia.

Warunek wg pierwszego stanu granicznego

q_rs ≤ m⋅q_f

q_rs -całkowite naprężenia działające w poziomie posadowienia

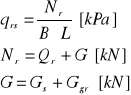
G_s-ciężar stopy

G_gr-ciężar

Objętość stopy

F=B⋅L=1,90⋅1,90=3,61 [m²]

f=0,60⋅0,60=0,36 [m²]

G_s = V_s⋅ρ_żelb⋅g = 1,58⋅2,40⋅9,81= 37,20 [kN]

V_gr = D_min⋅B²-V_s-( D_min-h) ⋅a_s [m³]

V_gr = 1,20⋅1,90²-1,58-(1,20-0,65) ⋅0,60 = 2,61 [m³]

G_gr = V_gr⋅ρ_gr ⋅g = 2,61⋅2,10_. ⋅9,81 = 53,77 [kN]

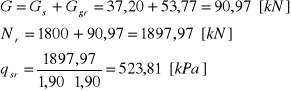
B = L = 1,9 0 [m]

D_min=1,20 [m]

ρ^r_D=1,72 [t/m³]

ρ^r_B = 1,59 [t/m³]

C^r_u = 0 [kPa] ∅^r_u = 26,82 [^Ο] N_C = 23,64 N_D = 12,96 N_B = 4,54

Opór jednostkowy:

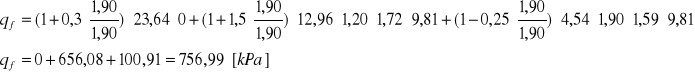
Sprawdzenie warunku

q_rs ≤ m⋅q_f

523,81 < 0,81⋅756,99

523,81 < 605,59 [kPa]

Pierwszy stan równowagi granicznej w poziomie posadowienia został zachowany.

Schemat obliczeniowy.

6. Sprawdzenie warunku wg drugiego stanu granicznego w stropie

warstwy słabej.

Schemat obliczeniowy.

h = 1.60 [m] < B = 1,90 [m] → b =

B' = L' = 1,90+0,53=2,43 [m]

N'_r= N_r+ B'⋅L'⋅ρ_h^r⋅g=1890,97 + 2,23⋅2,43⋅1, 87⋅9,81=1999,29 [kN]

q'_rs≤m⋅q'_f

D'_min.=2,80 [m]

B' = L' = 2,43 [m]

γ_m=0,9

ρ'^r_B=1,89 [t/m³] = ρ_sr → G_p

Określenie kąta tarcia wewnętrznego i kohezji:

G_P I_L:=0,26

C'ⁿ_u =14 [kPa]

∅'ⁿ_u=14 [^Ο]

C'^r_u = C'ⁿ_u *0,9=14*0,9=12,60 [kPa]

∅'^r_u=∅'ⁿ_u*0,9=14*0,9=12,60 [^Ο]

Współczynniki nośności:

N ^′_C=9,60

N ′_D=3,14

N ′_B=0,36

Opór jednostkowy:

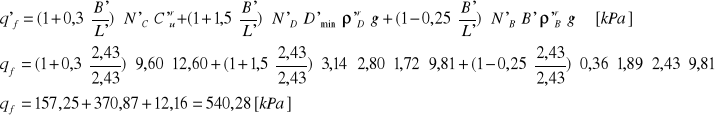
q'_rs ≤ m⋅q'_f

q'_rs = 338,58 [kPa] < m⋅q'_f = 0,81⋅540,28 = 437,63 [kPa]

Pierwszy stan równowagi granicznej w stropie warstwy słabej został zachowany.

7. Obliczenie naprężeń pierwotnych, wtórnych, dodatkowych i całkowitych.

Naprężenia pierwotne:

σ_zd ≤ 0,3⋅σ_zρ

σ_zd -naprężenia dodatkowe na głębokości z

σ_zρ -naprężenia pierwotne na głębokości z

Schemat obliczeniowy.

Naprężenia pierwotne:

σ_zρ=Σh⋅ρ⋅g [kPa]

σ_zρ0,50 = 0,50⋅2,42⋅9,81 = 11,87 [kPa]

σ_zρ1,20 = 11,87 + 0,70⋅1,87⋅9,81 = 24,71 [kPa]

σ_zρ2,00 = 24,71 + 0,80⋅1,87⋅9,81 = 39,39 [kPa]

σ_zρ2,80 = 39,39 + 0,80⋅1,87⋅9,81 = 54,07 [kPa]

σ_zρ3,40 = 54,07 + 0,60⋅2,31⋅9,81 = 67,67 [kPa]

σ_zρ4,23 = 67,67 + 0,83⋅1,23⋅9,81 = 77,69 [kPa]

σ_zρ5,05 = 77,69 + 0,82⋅1,23⋅9,81 = 87,58 [kPa]

σ_zρ5,88 = 87,58 + 0,83⋅1,23⋅9,81 = 97,59 [kPa]

σ_zρ6,70 = 97,59 + 0,82⋅1,23⋅9,81 = 108,21 [kPa]

Naprężenia wtórne:

σ_zs = σ_os⋅η_s [kPa]

η_s- współczynnik zaniku naprężeń

σ_os = σ_oρ= σ_zρ1,20 = 24,71 [kPa]

h = 1,20 [m] z = 0 ; z/B = 0 η_s = 1,00 σ_zs1,20 = 24,71⋅1,00 = 24,71 [kPa]

h = 1,60 [m] z = 0,40 ; z/B = 0,21 η_s = 0,75 σ_zs1,60 = 24,71⋅0,75 = 18,53 [kPa]

h = 2,40 [m] z = 1,20 ; z/B = 0,63 η_s = 0,42 σ_zs2,40 = 24,71⋅0,42 = 10,38 [kPa]

h = 3,10 [m] z = 1,90 ; z/B = 1, 00 η_s = 0,28 σ_zs3,10 = 24,71⋅0,28 = 6,92 [kPa]

h = 3,81 [m] z = 2,61 ; z/B = 1,37 η_s = 0,18 σ_zs3,81 = 24,71⋅0,18 = 4,45 [kPa]

h = 4,64 [m] z = 3,44 ; z/B = 1,81 η_s = 0,12 σ_zs4,64 = 24,71⋅0,12 = 2,97 [kPa]

h = 5,46 [m] z = 4,26 ; z/B = 2,24 η_s = 0,08 σ_zs5,46 = 24,71⋅0,08 = 1,98 [kPa]

h = 6,29 [m] z = 5,09 ; z/B = 2,68 η_s = 0,06 σ_zs6,29 = 24,71⋅0,06 = 1,48 [kPa]

Naprężenia dodatkowe:

σ_zd = η_s⋅ (q_rs-σ_oρ) [kPa]

q_rs = 523,81 [kPa]

σ_oρ = σ_zρ1,20 = 24,71 [kPa]

σ_zd = η_s⋅ (523,81-24,71) = η_s⋅495,32 [kPa]

σ_zd1,20 = 1,00⋅499,10 = 499,10 [kPa]

σ_zd1,60 = 0,75⋅499,10 = 374,33 [kPa]

σ_zd2,40 = 0,42⋅499,10 = 209,62 [kPa]

σ_zd3,10 = 0,28⋅499,10 = 139,75 [kPa]

σ_zd3,85 = 0,18⋅499,10 = 89,83 [kPa]

σ_zd4,64 = 0,12⋅499,32 = 59,89 [kPa]

σ_zd5,46 = 0,08⋅499,10 = 39,92 [kPa]

σ_zd6,29 = 0,06⋅499,10 = 29,95 [kPa]

Naprężenia wtórne na granicach warstw geotechnicznych:

h = 2,80 [m] z = 1,30 ; z/B = 0,68 η_s = 0,40 σ_zs2,80 = 24,71⋅0,40 = 9,88 [kPa]

h = 3,40 [m] z = 2,20 ; z/B = 1,16 η_s = 0,22 σ_zs3,40 = 24,71⋅0,22 = 5,44 [kPa]

h = 6,70 [m] z = 5,50 ; z/B = 2,89 η_s = 0,06 σ_zs6,00 = 24,71⋅0,06 = 1,48 [kPa]

Naprężenia dodatkowe na granicach warstw geotechnicznych:

σ_zs2,80 = 0,40⋅495,32 = 215,21 [kPa]

σ_zs3,40 = 0,22⋅495,32 = 116,02 [kPa]

σ_zs6,00 = 0,06⋅495,32 = 29,72 [kPa]

Sprawdzenie warunku σ_zd ≤ 0,3⋅σ_zρ

h = 6,70 [m] warstwa G_z

σ_zs6,70 = 29,95 [kPa] 0,3⋅σ_zρ = 0,3⋅142,45 = 42,74 [kPa]

Warunek został spełniony-do głębokości 6,70 m liczymy osiadania-sprawdzamy drugi stan graniczny.

Naprężenia całkowite:

σ_zt=σ_zρ+σ_zd [kPa]

σ_zt1,20=24,71 + 495,32 = 520,03 [kPa]

σ_zt2,80=54,07 + 198,13 = 252,20 [kPa]

σ_zt3,40=67,67 + 108,97 = 176,64 [kPa]

σ_zt6,70=108,21 + 29,72 = 137,93 [kPa]

8. Obliczenie spodziewanych osiadań. Sprawdzenie warunku wg drugiego stanu granicznego.

Osiadanie :

s=s'+s”

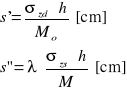
gdy λ=0 to

gdzie:

h - miąższość warstewek [cm]

M_o - moduł ściśliwości pierwotnej [kPa]

M - moduł ściśliwości wtórnej [kPa]

λ - współczynnik zależny od czasu wznoszenia budowli (równy 0 lub1)

Lp	Rodzaj gruntu	Miąższość warstwy h [cm]	Zagłębienie środka warstwy [m]	σzd [kPa]	Mo [kPa]	s [cm]
1	Pd ID=0,33	80	1,60	371,49	47000	0,632
2	Pd ID=0,33	80	2,40	208,03	47000	0,354
3	Gp IL=0,26	40	3,10	138,69	25500	0,218
4	Gp IL=0,26	83	3,81	89,16	255000	0,290
5	Gp IL=0,26	82	4,64	59,44	255000	0,191
6	Gp IL=0,26	83	5,46	39,63	25500	0,129
7	Gp IL=0,26	82	6,29	29,72	255000	0,096
					razem	1,910

Sprawdzenie drugiego stanu granicznego:

s≤s_dop s_dop=5,00 [cm]

s = 1,910 [cm] < s_dop=5,00 [cm].

Warunek drugiego stanu granicznego jest spełniony.

9. Obliczenie zbrojenia stopy.

Schemat obliczeniowy:

Metoda Labell'a.

Sprawdzenie warunku stosowalności metody:

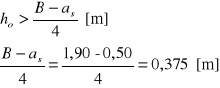
h₁=h-0,05 [m]

h₁=0,65 - 0,05 = 0,60 [m]

Warunek jest spełniony - możemy stosować tę metodę.

Siła rozciągająca - Z

Zapotrzebowanie na powierzchnię zbrojenia

stosujemy stal okrągłą, gładką klasy A-I

STAL - St 3Sx → R_a=210 [MPa]

F_a ≥ 25,00 [cm²]

Przyjęto zbrojenie:

13 ∅16

F_a = 13⋅2,011 = 26,143 [cm²]

Rozstawa zbrojenia

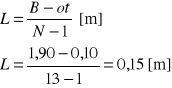
sprawdzenie warunku

10 [cm] ≤ L≤ ¼ ⋅h₁

10 [cm] = 15 [cm] ≤ ¼ ⋅h₁=15 [cm]

Warunek jest spełniony - rozstawa została zaprojektowana prawidłowo.

Zbrojenie słupa.

d-średnica zbrojenia

d = 20mm

e' = 20 cm = 10d = 20 cm

e = 30 cm < 15d = 60 cm

e = 30 cm < a_s = 60 cm

e = 30 cm < 40 cm

Warunki są spełnione.

G_p

I_L=0,08

P_d

I_D=0,33

G_p

I_L=0,26

G_p

I_L=0,17

P_r

I_L=0,14

3,40

0,50

2,80

6,00

9,70

12,50

0,65 m 0,05 0,50 0,05 0,65 m

B=1.90 [m]

h=2⋅B= 3.80 [m]

D_min=1,20 [m] ρ^r_D=1.72 [t/m³]

z=B=1.90 [m] ρ^r_B= 1.53 [t/m³]

0,55 m

0,40 m

0,65 m

w=0,25 m

D_min.=1,20 m

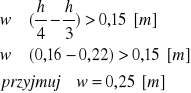
h

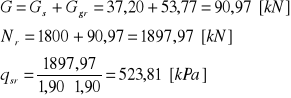
3,40

G_p

I_L=0,08

P_d

I_D=0,33

G_p

I_L=0,26

G_z

I_L=0,17

I_p

I_D=0,14

0,50

2,80

6,70

9,70

12,50

D_min=1,20 [m] ρ^r_D=1,72 [t/m³]

z=B=1,90 [m] ρ^r_B= 1,89 [t/m³]

B=1,90 [m]

1,30 [m]

0,50 [m]

0,50

2,80

6,70

9,70

12,50

G_p

I_L=0,08

P_d

I_D=0,33

G_p

I_L=0,24

G_z

I_L=0,30

I_p

I_D=0,40

3,40

D'_min=2,80 [m] ρ'^r_D=1,67 [t/m³]

ρ'^r_B= 1,89 [t/m³]

B=1,90 [m]

h=1,30 [m]

B'=2,43 [m]

z=2B=3,80 [m]

1,20

1,60

2,00

2,40

3,10

3,81

4,23

4,64

5,05

5,46

5,88

6,29

G_p

I_L=0,08

P_d

I_D=0,33

G_p

I_L=0,26

G_p

I_L=0,17

I_p

I_D=0,14

0,50

2,80

6,70

9,70

12,50

ρ^r=2,42 [t/m³]

ρ^r= 1,87 [t/m³]

ρ^r=2,31 [t/m³]

ρ^r=1,23 [t/m³]

ρ^r=1,23 [t/m³]

ρ^r=1,23 [t/m³]

B=1,90 [m]

z h

5cm

h₁ h_o

Q_r=1800kN

B=1,90 m

e=30cm

e'=20cm

e'=20cm

e'=20cm

3d = 6 cm

e=30cm

e=30cm

B = 1,90 m

a_sb

L

5-7cm

(otulina)

D_min=1,20 [m]

B=1.90 [m]

]

---