Katedra Geodezji i Astronomii Geodezyjnej Politechniki Warszawskiej Satelitarne techniki pomiarowe - ćwiczenia
ĆWICZENIE NR 3
TEMAT: Analiza problemów wynikających z transformacji współrzędnych
Wojtek Sadowski Studia II stopnia Grupa 2b wtorek 14:00-16:00	Data oddania: 12.06.2012 ………………………………	Zaliczenie: ………………………………

Zestawienie danych do zadania:

Nazwa pkt	x2000 [m]	y2000 [m]	B [˚]	L [˚]	Helip [m]	VRS	H nor k86[m]	Odstęp [m]
13206	5716314,841	7545023,087	51,579480	21,649553	143,675	0,016	110,870	32,805
13204	5717258,245	7543940,738	51,588045	21,634057	143,342	0,020	110,542	32,800
exc11203	5718963,078	7542687,724	51,603464	21,616184	143,199	0,016	110,456	32,743
exc124422	5712428,961	7538489,249	51,545036	21,554868	155,224	0,019	122,148	33,076
exc24201	5715450,497	7532843,974	51,572552	21,473770	183,065	0,024	149,860	33,205
exc24203	5715050,491	7535185,075	51,568815	21,507499	163,305	0,039	130,188	33,117
exc1253201	5713621,523	7544029,421	51,555350	21,634881	147,767	0,020	114,910	32,857
exc11201	5719725,321	7540677,160	51,610464	21,587252	141,184	0,021	108,380	32,804
exc22205	5720273,888	7539431,012	51,615483	21,569325	140,842	0,014	108,016	32,826
exc44209	5724043,225	7537859,895	51,649471	21,547049	140,31	0,019	107,532	32,778
exc1244450	5717376,567	7538424,637	51,589511	21,554478	147,271	0,046	114,229	33,042
124414	5718264,267	7536841,780	51,597596	21,531731	145,355	0,016	112,346	33,009
exc124417	5716403,166	7537930,820	51,580795	21,547247	149,353	0,022	116,393	32,960
exc124418	5716259,774	7537898,873	51,579509	21,546770	151,619	0,023	118,644	32,975
1244452	5714396,367	7536583,697	51,562847	21,527603	159,716	0,028	126,665	33,051
exc124420	5714540,487	7537575,830	51,564077	21,541926	157,336	0,021	124,296	33,040

Wstęp

Celem ćwiczenia było wyznaczenie odstępu geoidy od elipsoidy wykorzystując model geoidy (2001) oraz globalny model grawitacji (EGM2008). Wykorzystując polecony przez prowadzącego przedmiot program Geoida pozwala obliczyć składowe odchylenia linii pionu w analizowanych punktach jak także odstęp geoidy od elipsoidy. Posługując się globalnym modelem grawitacji oraz program EGM2008 Calculator wyznaczone zostały anomalie wysokościowe. Otrzymane wyniki przyrównano do wartości odstępu geoidy od elipsoidy obliczanej za pomocą różnic wysokości - elipsoidalnej i normalnej.

Nr	Helip	H nor k86	Odstęp	Geoida	Δ	EGM2008	Δ
10	143,675	110,870	32,805	32,805	0,000	32,761	0,044
11	143,342	110,542	32,800	32,811	0,011	32,794	0,006
12	143,199	110,456	32,743	32,802	0,059	32,785	0,042
13	155,224	122,148	33,076	33,104	0,028	33,078	0,002
14	183,065	149,860	33,205	33,187	0,018	33,157	0,048
15	163,305	130,188	33,117	33,131	0,014	33,104	0,013
16	147,767	114,910	32,857	32,900	0,043	32,864	0,007
17	141,184	108,380	32,804	32,841	0,037	32,824	0,020
18	140,842	108,016	32,826	32,863	0,037	32,849	0,023
19	140,31	107,532	32,778	32,806	0,028	32,781	0,003
20	147,271	114,229	33,042	32,975	0,067	32,961	0,081
1001	145,355	112,346	33,009	32,998	0,011	32,981	0,028
1002	149,353	116,393	32,960	33,016	0,056	32,988	0,028
1003	151,619	118,644	32,975	33,021	0,046	32,992	0,017
1004	159,716	126,665	33,051	33,109	0,058	33,082	0,031
1005	157,336	124,296	33,040	33,076	0,036	33,049	0,009

Na podstawie powyższego zestawienia można stwierdzić, że odstęp geoidy od elipsoidy wyznaczany z równania niwelacji satelitarnej niewiele różni się od wyniku otrzymanego z metody anomalii wysokości. Rozbieżności te są rzędu kilku centymetrów, co daje wynik zadowalający gdy rozpatrujemy wymagania standardowych pomiarów geodezyjnych.

Poniższe mapki przedstawiają izolinie różnic anomalii wysokości dla modelu Geoida 2001 oraz EGM2008:

Różnice anomalii wysokości dla modelu Geoida 2001

Różnice anomalii wysokości dla modelu Geoida 2001

Lokalny model quasi-geoidy

Aby uzyskać wartość odstępu geoidy od elipsoidy w dowolnym punkcie na określonym obszarze (zakres lokalny) niezbędnym jest utworzenie modelu geoidy. Można tego dokonać przybliżając jej powierzchnię do płaszczyzny (wielomian I stopnia) lub też paraboloidy (wielomian stopnia II).

Aproksymacja została wykonana metodą najmniejszych kwadratów. Równania obserwacyjne zrównoważono przyjmując za wagę odwrotność kwadratu błędu VRS.

- Aproksymacja do powierzchni płaszczyzny:

a
1		5716314,841	7545023,087
1		5717258,245	7543940,738
1		5718963,078	7542687,724
1		5712428,961	7538489,249
1		5715450,497	7532843,974
1		5715050,491	7535185,075
1		5713621,523	7544029,421
1		5719725,321	7540677,160
1		5720273,888	7539431,012
1		5724043,225	7537859,895
1		5717376,567	7538424,637
1		5718264,267	7536841,780
1		5716403,166	7537930,820
1		5716259,774	7537898,873
1		5714396,367	7536583,697
1		5714540,487	7537575,830
p
0,391
0,250
0,391
0,277
0,174
0,066
0,250
0,227
0,510
0,277
0,047
0,391
0,207
0,189
0,128
0,227

a1	430,792745
a2	-0,000028
a3	-0,000031

• współczynniki równania płaszczyzny (
  )
  

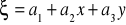
- Aproksymacja do powierzchni paraboloidy

a
1	-740,506		5833,278	548349,728	34027126,781	-4319579,346
1	202,898		4750,929	41167,436	22571321,929	963951,997
1	1907,731		3497,915	3639436,042	12235406,083	6673078,591
1	-4626,386		-700,560	21403451,122	490784,967	3241063,415
1	-1604,850		-6345,835	2575544,806	40269627,770	10184116,587
1	-2004,856		-4004,734	4019449,185	16037898,148	8028917,526
1	-3433,824		4839,612	11791150,010	23421839,794	-16618376,170
1	2669,974		1487,351	7128759,025	2212211,609	3971186,658
1	3218,541		241,203	10359003,594	58178,662	776320,146
1	6987,878		-1329,914	48830433,353	1768672,489	-9293279,512
1	321,220		-765,172	103182,031	585488,904	-245788,394
1	1208,920		-2348,029	1461486,599	5513242,376	-2838578,844
1	-652,181		-1258,989	425340,579	1585054,477	821089,513
1	-795,573		-1290,936	632937,035	1666516,961	1027034,714
1	-2658,980		-2606,112	7070176,768	6791822,189	6929601,969
2	-2514,860		-1613,979	6324522,831	2604929,719	4058933,047
p
0,391
0,250
0,391
0,277
0,174
0,066
0,250
0,227
0,510
0,277
0,047
0,391
0,207
0,189
0,128
0,227

	x
a0	32,92810699556
a1	-0,00002522997
a2	-0,00003435160
a3	-0,00000000069
a4	0,00000000107
a5	-0,00000000132

• współczynniki równania paraboloidy (
  )
  

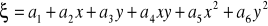
współrzędne bieguna transformacji

X0 = 5717055,347

Y0 = 7539189,809

Analiza dokładności otrzymanych wyników:

Nazwa	Helip	H nor k86	odstep	model płaszczyzny	∆ξ [m]	model paraboloidy	∆ξ [m]
10	143,675	110,870	32,805	32,773	0,032	32,788	0,017
11	143,342	110,542	32,800	32,780	0,020	32,783	0,017
12	143,199	110,456	32,743	32,770	0,027	32,762	0,019
13	155,224	122,148	33,076	33,087	0,011	33,050	0,026
14	183,065	149,860	33,205	33,178	0,027	33,215	0,010
15	163,305	130,188	33,117	33,116	0,001	33,120	0,003
16	147,767	114,910	32,857	32,880	0,023	32,887	0,030
17	141,184	108,380	32,804	32,812	0,008	32,802	0,002
18	140,842	108,016	32,826	32,835	0,009	32,831	0,005
19	140,310	107,532	32,778	32,777	0,001	32,778	0,000
20	147,271	114,229	33,042	32,949	0,093	32,947	0,095
124414	145,355	112,346	33,009	32,973	0,036	32,987	0,022
exc124417	149,353	116,393	32,960	32,992	0,032	32,988	0,028
exc124418	151,619	118,644	32,975	32,997	0,022	32,993	0,018
1244452	159,716	126,665	33,051	33,091	0,040	33,078	0,027
exc124420	157,336	124,296	33,040	33,056	0,016	33,040	0,000

	Model płaszczyzny	Model paraboloidy
max	0,093	0,095
min	0,001	0,000

---