Temat: Elektrony poruszające się wzdłuż łańcucha

Opis modelu

Jak dotąd badane przez nas układy mogły się znajdować w dwóch stanach. Obecnie zajmiemy się układem, który może się znajdować w
stanach. Przyjmijmy, że cząstka (nie koniecznie atom azotu, może być to np. elektron) może znajdować się w punktach nieskończonego łańcucha leżącego na osi x. Cząstka może znaleźć się w punktach
. Odległość b dzieląca sąsiednie węzły nazywa się stałą sieci.

Rys. 12.1

Tę sytuację można np. zrealizować w następujący sposób. W węzłach liniowego łańcucha należy umieścić atomy takiego samego rodzaju. Do jednego z nich, np. n-tego należy dodać elektron, zamieniając go w ten sposób w jon. Podobnie jak było z atomem azotu w cząstce amoniaku, elektron z pewnym prawdopodobieństwem może przeskoczyć do innego węzła. Niech
będzie wektorem stanu tego układu odpowiadającym stanowi: we wszystkich węzłach oprócz n-tego znajdują się atomy. Tylko w n-tym węźle znajduje się atom i elektron - jon. Ponieważ elektron musi się znajdować w którymś z węzłów łańcucha więc zbiór n wektorów

tworzy bazę stanów fizycznych. Dowolny stan
badanego układu można zapisać w postaci superpozycji [1]

.

Gdy w ten sposób będziemy określali wektory stanu będziemy mówili o reprezentacji poło­żeń.

Załóżmy dla prostoty, że elektron znajdujący się w n-tym węźle może przeskoczyć do najbliższych węzłów
, natomiast do węzłów

nie może (taka sytuacja ma miejsce np. gdy prawdopodobieństwo przeskoku wykładniczo maleje z odległością pomiędzy atomami). Rozważane uproszczenie nazywa się przybliżeniem oddziaływania najbliższych sąsiadów. Podobnie jak w przypadku cząstki amoniaku przyjmiemy, że
jest amplitudą prawdopodobieństwa przeskoku z n-tego do
węzła (i oczywiście z
w n w ciągu jednostkowego interwału czasu. Równanie Schrödingera (tj. równanie bilansu dla amplitudy prawdopodobieństwa znalezienia elektronu koło n - tego węzła) ma podobną postać jak równanie dla atomu azotu w

, (12.1a)

jest energią układu gdy elektron jest zlokalizowany w pobliżu któregoś z atomów i nie zmienia położenia. Lecz elektron może przeskoczyć z
do
itd. Należy więc napisać równania dla dwóch sąsiednich węzłów

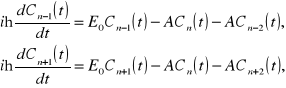
(12.2b)

itd. Po przypomnieniu sobie własności równań dla cząstki amoniaku zauważymy, że gdy
poziom energetyczny jest N-krotnie zwyrodniały. Kierując się formalnym podobień­stwem układu równań (12.1) i równań (11.13) możemy napisać macierz reprezentującą Hamiltonian rozważanego układu

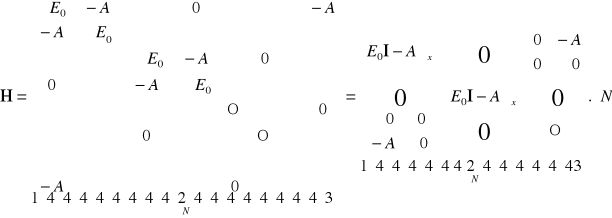
(2.3)

By nie rozpatrywać nieskończonych obiektów założymy, że łańcuch się składa z N atomów, a na
oraz
nałożymy odpowiednie warunki, np.

.

Są to cykliczne warunki brzegowe Borna-Karmana (rys. 12.2). W wyniku nałożenia cyklicznych warunków brzegowych hamiltonian staje się macierzą
. Jest to macierz kwazidiagonalna, gdyż na jej diagonali znajdują się macierze
. Długość L łańcucha wynosi
.

Rys. 12.2

12.2 Postać amplitud C_n(t)

Powrócimy do ruchu elektronów wzdłuż węzłów łańcucha. Dla zbioru amplitud
wprowadzimy oznaczenie

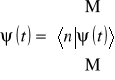
. (12.6)

Wektor
spełnia równanie Schrödingera

. (12.7)

Zbadamy teraz własności symetrii układu. Rozpatrywany łańcuch jest strukturą okresową. W przypadku nieskończonego łańcucha lub łańcucha z cyklicznymi warunkami brzegowymi można przesunąć argumenty wszystkich amplitud
o
gdzie m jest dowolną liczbą całkowitą, a równania nie ulegną zmianie. Wprowadzimy
- operator translacji (przeniesienia) stanu węzłów łańcucha o m węzłów, tj. o odcinek

. (11.8)

Operator translacji spełnia oczywiste związki

. (12.9a)

Dla każdego węzła l łańcucha o N atomach i cyklicznych warunków brzegowych spełnione są warunki

. (12.9b)

Aby warunek (11.8) był spełniony amplituda
musi mieć postać

, (12.10a)

gdzie

. (12.10b)

Od numeru węzła zależy jedynie, niezależny od czasu, czynnik a_n. Na mocy warunku (12.8) mamy

.

Lecz
, skąd otrzymujemy warunek

.

Stwierdzamy więc, że
, skąd wynika, że
, gdzie
., a to oznacza, że

. (12.11)

Pokażemy, że
. Rozpatrzymy liczbę kqb dla

,

i odpowiedni czynnik fazowy
. Zatem stwierdzamy, że istnieje N dozwolonych różnych wartości wektora falowego k. Ponieważ mamy do czynienia z zagadnieniem jednowymiarowym liczba falowa k jest jednocześnie wektorem falowym (który ma jedną składową). Przyjmiemy je w postaci

. (12.12)

Liczba falowa k jest liczbą kwantową pozwalający klasyfikować stany energii w krysztale. Gdyby elektron poruszał się w jednowymiarowej strukturze nieokresowej

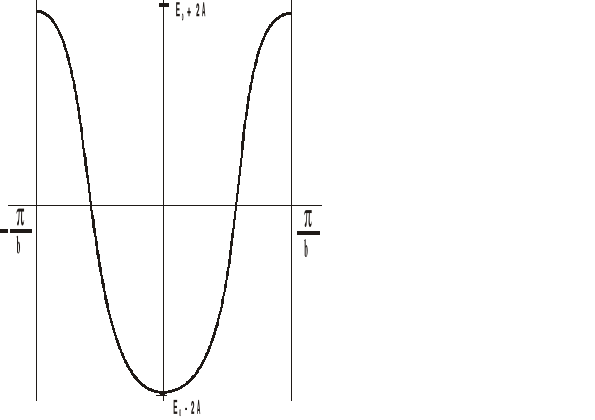
Rys. 12.3

Wartościom
odpowiadają maksymalne liczby falowe

. (12.13)

12.4 Granica ośrodka ciągłego

Dla skończonego łańcucha dopuszczalne są tylko dyskretne wartości (12.11) wektora falo­we­go k_q, a więc i dyskretne energii

. Dopuszczalne wartości wektora falowego zajmują węzły łańcucha w jednowymiarowej przestrzeni pędów (przestrzeni odwrotnej). Odległości pomiędzy sąsiednimi węzłami są jednakowe i wynoszą
. Widzimy, że im większa jest długość L łańcucha tym bardziej gęsto ułożone są węzły sieci odwrotnej. Rozpatrzymy różnicę pędów
i energii
, a także ilorazy
,
. Na podstawie wzoru (12.11) stwierdzamy, że

.

Podobnie ze wzoru (12.15a) wynika oszacowanie

,

słuszne dla n>>1 (tj. dla N>>1). Dla takich n obydwa te ilorazy są bardzo małe. Możemy powiedzieć, że widmo pędów i widmo energii elektronu dla dużych wartości n w sieci jest kwaziciągłe, wartości tych wielkości ułożone są gęsto. Na jeden punkt w przestrzeni odwrotnej wypada odcinek o długości
. Wybierzemy dowolny obszar
przestrzeni odwrotnej o dostatecznie dużej “objętości” (tj. długości)
. “Objętość”, tj. długość,
elementarnej komórki w przestrze­ni odwrotnej równa jest
. Zatem w obszarze
znajduje się
komórek. To oznacza, że w elemencie dk znajduje się
punktów. Jak widać
jest gęstością stanów pędu w jednowymiarowej przestrzeni odwrotnej. Tę gęstość oznaczymy przy pomocy litery ν

. (12.14)

Podobnie gęstość stanów pędu
. Niech
będzie dostatecznie regularną funkcją wektora falowego. Zbadajmy sumę
. Ponieważ widmo wektorów k jest kwaziciągłe można zamienić w I sumę na całkę

, (12.15)

gdzie
.

12.4 Widmo energii cząstek w krysztale

Powrócimy do równań (12.12) dla amplitud postaci (12.10). Po podzieleniu obydwu stron przez czynnik
otrzymamy równanie pozwalające wyrazić energię elektronu w sieci przez zbiór wielkości charakteryzujących ten układ. Są nimi E₀, A, b

. (12.14)

Związek (12.14) nazywamy prawem dyspersji dla elektronu w sieci krystalicznej. Dla małych argumentów
, a więc gdy

.

Warunek, który nałożyliśmy na liczbę falową k można przekształcić w warunek dla długości fali

.

Ponieważ elektron w sieci krystalicznej nie jest zlokalizowany amplitudy prawdopodobieńst­wa mają własności falowe. Gdy długość “fali amplitud prawdopodobieństwa” λ jest znacznie większa od stałej sieci b

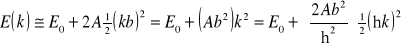
. (12.15a)

Za De Broglie możemy przyjąć, że pęd p cząstki poruszającej się wzdłuż łańcucha równy jest
, wobec tego jej energia składa się z dwóch składników
, gdzie
. Wielkość
spełnia związek

. (12.15b)

przypominający ten, który łączy energię cząstki swobodnej z pędem. Związek (12.15b) nazywamy kwadratowym prawem dyspersji. Stwierdzamy więc, że prawo dyspersji dla cząstki w sieci krystalicznej jest kwadratowe. Zbadajmy wymiar fizyczny współczynnika m^*

. (12.16)

Z równań (12.12) dla amplitud wynika, że
ma wymiar fizyczny odwrotności czasu
, natomiast
, zatem

.

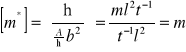
Ponieważ współczynnik m^* ma wymiar masy nazywamy go masą efektywną elektronu w sieci. Ta masa może różnić się od masy m_e elektronu w próżni
. Zależy ona od stałej sieci b i od stałej oddziaływania A powodującego delokalizację cząstki. Im współczynnik A jest większy tym łatwiej cząstka przeskakuje z węzła na węzeł i tym mniejsza jest masa efektywna
.

Wielkość
nazywana jest szerokością pasma energii cząstki w krysztale. Zauważymy, że
, zatem współczynnik delokalizacji A usuwa N-krotne zwyrodnienie poziomu energii E₀, który rozczepia się w całe pasmo o szerokości proporcjonalnej do A. Wyrażenie
ma sens charakterystycznej prędkości v z jaką poruszają się elektrony w sieci. Zapiszemy ją w postaci
. Z równania (12.15a) wynika, że iloraz
ma wymiar czasu. Ten czas nazwiemy czasem delokalizacji, jest on odwrotnie proporcjonalny do A

.

Im większy jest współczynnik delokalizacji tym krótszy jest charakterystyczny czas
i tym większe jest prawdopodobieństwo przeskoku w ciągu jednostkowego interwału czasu
. Ponieważ „przeskakiwanie” jest zjawiskiem kwantowym oczekujemy, że w granicy klasycznej gdy
częstość przeskoków w_d powinna znikać, a charakterystyczny czas przeskoku
powinien rosnąć w sposób nieograniczony. Jest to możliwe jeżeli
.

Zauważymy, że w rzeczywistości rozpatrywaliśmy własności niezlokalizowanego stanu jonizacji atomów sieci. Rzecz jasna można sobie wyobrazić inne niezlokalizowane własności sieci, np. stan momentu magnetycznego cząstek znajdujących się w węzłach, albo wręcz niezlokalizowane miejsce niezajęte przez atom (lukę w sieci). Każdy z takich niezlokalizowanych stanów można uważać za niby cząstkę - kwazicząstkę, przy czym prawo dyspersji nie zawsze musi być kwadratowe, a nawet gdy jest kwadratowe to ma charakter anizotropowy

.

Ponieważ masa efektywna nie jest związana z bezwładnością może być także ujemna
.

Całkę (12.15) można przekształcić tak by całkowanie przebiegało po energiach

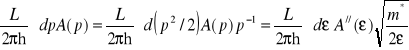
, (12.16)

gdzie
. Jak widać gęstość stanów energii układu jednowymiarowego
równa jest

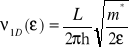
. (12.17)

Literatura

[1] [1] R.P. Feynman, R.B. Leighton, M. Sands, Feynmana wykłady z fizyki, Warszawa, PWN, 1972, R. 9.

[2] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading, Mass., 1974, R. 1.

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

|n-3>

(n+2)

n

(n+1)

(n-1)

b

x

4

N-1

3

1

2

---