Politechnika Wrocławska Instytut Fizyki |
Sprawozdanie ćw nr 8
Temat: Wyznaczanie współczynnika lepkości cieczy na podstawie prawa Stokesa.
|
|
Wydział Budownictwa Lądowego i Wodnego Rok I |
Data wykonania ćw:
07.04.2009r. |
Ocena: |
1.Wstęp teoretyczny.
Lepkością(tarciem wewnętrznym) nazywamy zjawisko występowania sił stycznych przeciwstawiających się przemieszczaniu się jednych części ciała względem innych jego części. W wyniku działania siły tarcia wewnętrznego występującego między warstwami cieczy, poruszająca się warstwa pociąga ze sobą warstwy sąsiadujące z nią. Dzięki ruchom cieplnym cząsteczek, mamy doczynienia z transportem pędu miedzy warstwami poruszającymi się z różną prędkością. Wszystkie rzeczywiste ciecze są lepkie, co odgrywa znaczącą rolę w ruchu ciała stałego w ośrodku ciekłym.
Przepływ cieczy nazywamy ustalonym, gdy jej prędkość w każdym punkcie ośrodka nie jest zależna od czasu. W przypadku gdy strumień stanowi zespół warstw przemieszczających się jedna względem drugiej jest to tak zwany przepływ laminarny. W przypadku gdy prędkość przepływu przekroczy pewną wartość krytyczną dla danej substancji następuje mieszanie różnych warstw cieczy, co powoduje powstawanie wirów, ruch taki nazywamy turbulentnym-wirowym.
Wzór opisujący zależność siły tarcia wewnętrznego od współczynnika lepkości (��) ma postać:
[��]=
Dla cieczy zależność współczynnika lepkości od temperatury ma postać:
��=C
,
gdzie C i b to stałe charakterystyczne dla danej cieczy.
Doświadczalnie stwierdzono, że dla małych prędkości Ft jest wprost proporcjonalna do prędkości, zależy od charakterystycznego wymiaru liniowego ciała l oraz współczynnika lepkości cieczy ��.
Stąd prawo Stokesa dla kulki o promieniu r:
Ale na kulkę spadającą swobodnie w cieczy działają również inne siły, a mianowicie siła wyporu oraz ciężar kulki. Wówczas równanie kulki ma postać:
Z którego otrzymujemy:
Vg-prędkość graniczna
Wzór ten jest słuszny dla obszaru nieograniczonego cieczy. Jeśli badana ciecz znajduje się w naczyniu należy uwzględnić działania ścianek na kulkę. Dla warstwy cieczy o wysokości H, znajdującej się w naczyniu cylindrycznym o promieniu R, otrzymujemy:
Uwzględniając dwa ostatnie wzory gdy:
=0 ∧
=0 możemy w przypadku kulki spadającej w cieczy przedstawić współczynnik lepkości w postaci:
k-stała określająca warunki doświadczenia
t-czas przebycia drogi ruchem jednostajnym.
2.Cel ćwiczenia.
Badanie ruchu ciał spadających w ośrodku ciekłym, wyznaczanie współczynnika lepkości cieczy metodą Stokesa, wyznaczanie zależności współczynnika lepkości cieczy od temperatury za pomocą wiskozymetru Höpplera.
3.Przebieg ćwiczenia.
a) Pomiar lepkości cieczy metodą Stokesa za pomocą szerokiego cylindrycznego naczynia szklanego.
Osuszone i wyczyszczone kulki zważono na wadze oraz zmierzono ich średnice śrubą mikrometryczną. Za pomocą linijki została zmierzona odległość między pierścieniami.
Ćwiczenie polegało na wielokrotnym zmierzeniu czasu spadania kulek na drodze h. Kulki te były puszczane swobodnie tuż nad powierzchnią cieczy. Na koniec areometrem zmierzono gęstość badanej cieczy.
Układ pomiarowy:
b) Pomiar lepkości cieczy metodą Stokesa za pomocą wiskozymetru Höpplera.
Po zbadaniu temperatury badanej cieczy kilkakrotnie zmierzono czas spadania kulki na drodze między skrajnymi kreskami znaczącymi.
Układ pomiarowy:
Obliczenia pomiarowe
Naczynie cylindryczne
Do obliczenia niepewności pomiaru gęstości użyto różniczki zupełnej:
![]()
Z kilkukrotnie zmierzonej średnicy kuli obliczamy jej średnią wartość:
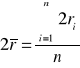
Błąd średniej długości średnicy obliczamy przy użyciu różniczki zupełnej:
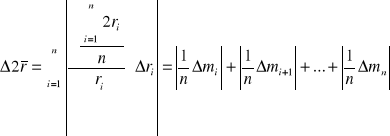
Długość promienia obliczono poprzez podzielenie długości średnicy przez 2 a do obliczenia błędu promienia wykorzystaną różniczkę zupełną:
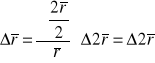
Czas średni obliczamy z średniej arytmetycznej:

Niepewność wyliczonego czasu średniego:
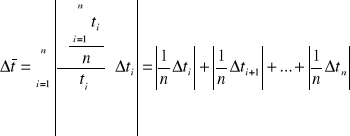
Gęstość kulki obliczamy ze wzoru:
![]()
Niepewność tej gęstości obliczamy wzorem podanym wcześniej. Do obliczenia współczynnika lepkości skorzystano ze wzoru:
![]()
Błąd tego współczynnika wyliczony został ze wzoru:

Średnią wartość η obliczono z średniej arytmetycznej a błąd ze wzoru:
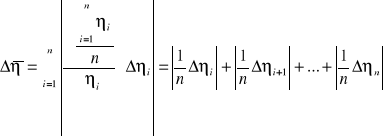
Wiskometr
Wzór na współczynnik lepkości:
![]()
Niepewność η wyznaczamy wzorem:
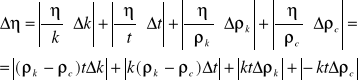
Wyszukiwarka
Podobne podstrony:
Ćw 8 Wyznaczanie współczynnika lepkości cieczy na podstawie prawa Stokesa
Sprawozdanie 8 Wyznaczanie współczynnika lepkości cieczy na podstawie prawa Stokesa
Wyznaczanie współczynnika lepkości cieczy na podstawie prawa stokesa, laborki
WYZNACZANIE WSPÓŁCZYNNIKA LEPKOŚCI CIECZY NA PODSTAWIE PRAWA STOKES’A
008 Wyznaczanie współczynnika lepkości cieczy na podstawie prawa Stokesa sprawozdanie
Wyznaczanie współczynnika lepkości cieczy na podstawie prawa Stokesa
cw 15 - Wyznaczanie współczynnika lepkości cieczy za pomocą wiskozymetru Stockes’a, Sprawozdania j
Wyznaczanie współczynnika lepkości cieczy biologicznych metodą opartą na prawie Stokesa
,laboratorium podstaw fizyki,Wyznaczanie współczynnika lepkości cieczy
wyznaczenie współczynnika lepkości na podstawie prawa Stokesa, Uczelnia PWR Technologia Chemiczna, S
08 Wyznaczanie współczynnika lepkości na podstawie prawa Stokesa
,Laboratorium podstaw fizyki, Wyznaczanie współczynnika lepkości cieczy metodą Stokesa
Excel Ćw 8 Wyznaczanie współczynnika lepkości cieczy metodą Stokesa
08 Wyznaczanie współczynnika lepkości na podstawie prawa Stokesa
Wyznaczanie współczynnika lepkości cieczy metodą Ostwalda, Fizyka
OI04 Wyznaczanie wspolczynnika lepkosci cieczy metoda Stokesa
Wyznaczanie współczynnika lepkości cieczy biologicznych metodą Stokesa
Ćw nr 4, cw36, POMIAR LEPKOŚCI CIECZY 36
więcej podobnych podstron