P1. RÓWNANIE O ZMIENNYCH ROZDZIELONYCH
![]()
[zazwyczaj ![]()
]
P2. RÓWNANIE JEDNORODNE WZGLĘDEM x I y
![]()
P3. RÓWNANIE LINIOWE
![]()
P4. RÓWNANIE BERNOULLIEGO
![]()
P5. UKŁAD RÓWNAŃ O STAŁYCH WSPÓŁCZYNNIKACH, JEDNORODNY
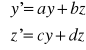
P6. UKŁAD RÓWNAŃ O STAŁYCH WSPÓLCZYNNIKACH NIEJEDNORODNY
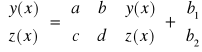
P7. RÓWNANIA WYŻSZYCH RZĘDÓW JEDNORODNE
![]()
P8. RÓWNANIA WYŻSZYCH RZĘDÓW NIEJEDNORODNE
![]()
P7. WZORY
P1. RÓWNANIE O ZMIENNYCH ROZDZIELONYCH
![]()
[zazwyczaj ![]()
] D=…
Sprawdzamy g(y)=0 y=a
Definiujemy funkcję y(x)=a dla ![]()
Zatem funkcja ta jest rozwiązaniem równania
Załóżmy, że ![]()
![]()
![]()
![]()
…
![]()
P2. RÓWNANIE JEDNORODNE WZGLĘDEM x I y
![]()
D=…
Niech ![]()
=> ![]()
![]()
![]()
I otrzymujemy równanie o zmiennych rozdzielonych
Obliczamy a na końcu podstawiamy ![]()
P3. RÓWNANIE LINIOWE
![]()
D=…
Jest to równanie liniowe w którym p(x)=…, g(x)=..
Szukamy kolejno
1° rozwiązania równania ![]()
![]()
![]()
Ale szybciej jest ze wzoru ![]()
, ![]()
, dla ![]()
…
2° ![]()
METODA UZMIENNIANIA STAŁEJ
![]()
![]()
Podstawiamy do ![]()
i wyznaczamy ![]()
(lub ![]()
i całkujemy)
![]()
METODA PRZEWIDYWAŃ GDY ![]()
i ![]()
ma postać:
I) ![]()
, k=1 gdy ![]()
II) 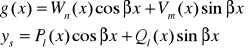
, l=max(n,m)
III) 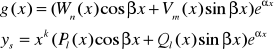
k=1 gdy ![]()
i ![]()
Mamy ![]()
…
![]()
Podstawiamy do głównego wzoru
![]()
BONUS
Gdy ![]()
![]()
![]()
![]()
P4. RÓWNANIE BERNOULLIEGO
![]()
,
Gdy ![]()
stała funkcja ![]()
jest rozwiązaniem równania
Szukamy rozwiązania ![]()
![]()
![]()
![]()
![]()
I mamy równanie liniowe
P5. UKŁAD RÓWNAŃ O STAŁYCH WSPÓŁCZYNNIKACH, JEDNORODNY
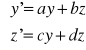
![]()
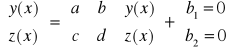
Jest to układ równań liniowych o stałych współczynnikach, jednorodny
Równanie charakterystyczne ma postać
![]()
, gdzie E-macierz jednostkowa
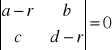
![]()
, ![]()
Dla r1=.. o kr(r1)=.. szukamy rozwiązania w postaci
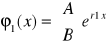
dla kr=1 lub 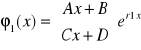
dla kr=2
Następnie wstawiamy do układu
![]()
![]()
Dla r2=… …
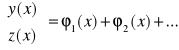
P6. UKŁAD RÓWNAŃ O STAŁYCH WSPÓLCZYNNIKACH NIEJEDNORODNY
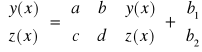
1° Szukamy rozwiązania ogólnego
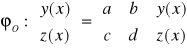
2°Szykamy ![]()
rozwiązania szczególnego układu pełnego
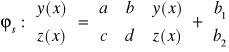
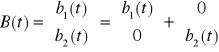
Szukamy rozwiązania
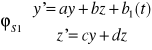
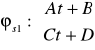
dla b(t)=t lub 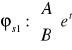
dla b(t)=e^t (a jak coś nie pasuje to zwiększamy stopień wielomianu)
![]()
Wyliczamy współczynniki podstawiając do wzoru
P7. RÓWNANIA WYŻSZYCH RZĘDÓW JEDNORODNE
![]()
D=…
Równanie charakterystyczne
![]()
…
![]()
![]()
… tyle pierwiastków jaka krotność i każdy kolejny pomnożony przez x
![]()
dla ![]()
, gdzie ![]()
JEŻELI:
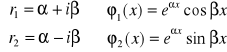
P8. RÓWNANIA WYŻSZYCH RZĘDÓW NIEJEDNORODNE
![]()
1° Szukamy rozwiązania ogólnego
![]()
![]()
2° ![]()
METODA UZMIENNIANIA STAŁEJ
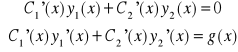
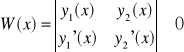
Z tw. Cramera
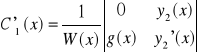
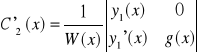
METODA PRZEWIDYWAN
I)![]()
, k - krotność pierwiastka ![]()
równania charakterystycznego
II) ![]()
gdzie l=max(n,m), k=1 gdy ![]()
jest pierwiastkiem równaniacharakterystycznego
III)![]()
gdzie l=max(n,m), a k oznacza krotność pierwiastka ![]()
równania charakterystycznego
RÓŻNE:
![]()
![]()
![]()
![]()
Przez części: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
sciaga rownanie rozniczkowe zupelne, AGH, I & II, Matematyka, Teoria
sciaga rownanie rozniczkowe o zmiennych rozdzielonych, AGH, I & II, Matematyka, Teoria
1296581494 Matematyka definicje-Szybowski-zimowy iman, AGH, I & II, Matematyka, Egzamin 1
10 - Dynamika rucha obrotowego bryly - Teoria, AGH, I & II, Fizyka, Teoria
definicje-Szybowski-zimowy, AGH, I & II, Matematyka, Egzamin 1
definicje - Kopia, AGH, I & II, Matematyka, Egzamin 1
mata teoria, Politechnika Slaska, studia zaoczne, rybnik, wydzial gornictwo i geologia, semestr II,
mata roler, Politechnika Slaska, studia zaoczne, rybnik, wydzial gornictwo i geologia, semestr II, m
więcej podobnych podstron