Definicja granicy ciągu liczbowego i jej własności: lim{n→oo} an=a ⇔ ∧{ε>0} ∨{No∈N} ∧{n≥No} |an-a|<ε. Własności: 1) Jeżeli ciąg ma granicę, to ma ją tylko jedną. 2) Jeżeli ciąg {an} ma granicę to każdy podciąg wybrany z tego ciągu ma również taką samą granicę. 3) Każdy ciąg zbieżny jest ograniczony. 4) Każdy ciąg monotoniczny i ograniczony jest zbieżny. Podstawowe własności funkcji. Funkcja jest: 1) rosnąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)<f(x2). 2) niemalejąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)≤f(x2). 3) malejąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)>f(x2). 4) nierosnąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)≥f(x2). 5) stała w A⊂Df ⇔ ∧{x1,x2∈A} x1≠x2 ⇒ f(x1)=f(x2). 6) parzysta ⇔ ∧{x∈Df} (-x)∈Df ∧ f(-x)=f(x) wykres f parzystej jest symetryczny względem osi y. 7) nieparzysta ⇔ ∧{x∈Df} (-x)∈Df ∧ f(-x)=-f(x) wykres f nieparzystej jest symetryczny względem początku układu współrzędnych. 8) okresowa o okresie podstawowym To(To≠0) ⇔ ∧{x∈Df} (x+To) ∈ Df ∧ f(x+To)=f(x). 9) ograniczona z góry ⇔ ∨{M∈R} ∧{x∈Df} f(x)≤M; ograniczona z dołu ⇔ ∨{M∈R} ∧{x∈Df} f(x)≥M. Funkcja jest ograniczona, gdy jest ograniczona z góry i z dołu. F. odwrotna: def. Niech f: A na→ B. Funkcją odwrotną do funkcji f nazywamy taką funkcję g, która odwzorowuje teraz zbiór B na→ A. ∧{x∈A} ∧{y∈B} y=f(x) ⇔ x=g(y). Tw. Jeżeli f: A na→ B jest różnowartościowa, to istnieje do niej funkcja odwrotna g przeprowadzająca zbiór B na→ A. Symbol: g(x)=f-1(x).

Asymptoty wykresu funkcji: 1) Def. Prosta x=a jest asymptotą pionową (lewostronną) wykresu funkcji y=f(x) ⇔ lim{x→a+}{x→a-}f(x)=+-oo. Jeżeli prosta x=a jest asymptotą pionową prawostronną i lewostronną, to nazywany ją obustronną. 2) Def. Niech f•x∈(xo, +oo). Prosta y=mx+p jest asymptotą ukośną prawostronną wykresu f: y=f(x) ⇔ lim{x→oo} [f(x)-(mx+p)]=0. Niech f•x∈(-oo, x1). Prosta y=mx+p jest asymptotą ukośną lewostronną wykresu f: y=f(x) ⇔ lim{x→-oo} [f(x)-(mx+p)]=0. 3) Szczególnym przypadkiem asymptoty ukośnej jest asymptota pozioma. Prosta y=p jest asymptotą poziomą prawostronną (lewostronną) ⇔ lim{x→+oo}{x→-oo} f(x)=p. Twierdzenie: Prosta y=mx+p jest a.ukośną prawostronną (lewostronną) ⇔ 1) lim{x→+oo}{x→-oo} f(x)•1/x=m. 2) lim{x→+oo}{x→-oo} [f(x)-mx]=p. Ciągłość funkcji w punkcie i przedziale. A) Def. Funkcja f jest ciągła w punkcie xo ⇔ 1) xo∈Df (jest określona w tym punkcie); 2) lim{x→xo} f(x)=a (ma skończoną granicę); 3) lim{x→xo} f(x)=f(xo) (granica ma taką samą wartość w tym punkcie). xo∈(a,b) ⊂ Df. Definicja odnosi się do punktów nieizolowanych dziedziny. Jeżeli w Df istnieją punkty izolowane Df=(c,d)∪″{xo}″, wtedy w tych punktach z definicji przyjmujemy, że funkcja jest ciągła. B) Funkcja jest ciągła w przedziale <c,d> ⇔ gdy jest ciągła w przedziale (c,d) i lim{x→c+} f(x)=f(c) ∧ lim{x→d-} f(x) = f(d). Twierdzenia o funkcjach ciągłych: 1) Jeżeli f jest ciągła w <a,b>, to przyjmuje w tym przedziale wszystkie wartości pomiędzy f(a), f(b). 2) Jeżeli f jest ciągła w <a,b>, to przyjmuje w tym przedziale swoją wartość największą i najmniejszą. 3) Jeżeli f jest ciągła w <a,b>, i f(a)-f(b)<0, to ∨{c∈(a,b)} f(c)=0.

Reguły różniczkowania. A) (f(x)+g(x)) ` = f ` (x)+g ` (x). B) (α•f(x)) '  = α•f ` (x), α∈R. C) (f(x)•g(x)) ` = f ` (x)•g(x)+f(x)•g ` (x). D) (f(x)/g(x)) ` = (f ` (x)•g(x)-g ` (x)•f(x))/(g(x))2. Tw. Lagrange'a i wnioski: Niech f jest: 1) ciągła w <a,b> 2) różniczkowalna w (a,b) to ∨{c∈(a,b)} f ` (c)=(f(b)-f(a))/(b-a) RYS (f(b)-f(a))/(b-a)=tgβ. Wnioski: 1) Jeżeli funkcja jest różniczkowalna w (a,b) i f ` (x)>0, to funkcja jest rosnąca w (a,b). 2) Jeżeli funkcja jest różniczkowalna w (a,b) i f ` (x)<0, to funkcja jest malejąca w (a,b). 3) Jeżeli funkcja jest różniczkowalna w (a,b) i f ` (x)=0, to funkcja jest stała. 4) Jeżeli funcje f i g są różniczkowalne w (a,b) i w każdym punkcie tego przedziału f ` (x)=g ` (x), to funkcje różnią się tylko o stałą. Wykresy są równoległe: f(x)=g(x)+c w (a,b); c∈R. Ekstrema lokalne i warunek konieczny. Funkcja f(x) ma w punkcie xo (xo∈Df) maksimum lokalne ⇔ ∨{Sxo} ∧{x∈Sxo} f(x) ≤ f(xo). Funkcja f(x) ma w punkcie xo minimum lokalne ⇔ ∨{Sxo} ∧{x∈Sxo} f(x) ≥ f(xo). Jeżeli nierówności występujące w definicji są ostre, to mówimy, że funkcja ma max i min (ekstremum) lokalne właściwe. Tw. Warunek konieczny ekstremum funkcji: Jeżeli funkcja jest różniczkowalna w pewnym otoczeniu punktu xo (Uxo) i ma w xo ekstremum lokalne, to f'(xo)=0. Uwaga: Dla funkcji różniczkowalnych ekstrema lokalne mogą istnieć tylko w punktach zerwania się pierwszej pochodnej. Warunek wystarczający extremum (tw.) Jeżeli funkcja jest różniczkowalna w Uxo oraz: 1) f '(xo)=0; ∧{x∈S-xo} f '(x)>0; ∧{x∈S+xo} f `(x)<0; to f ma w xo maksimum lokalne, oraz 2) f `(xo)=0; ∧{x∈S-xo} f '(x)<0; ∧{x∈S+xo} f `(x)>0; to f ma w xo minimum lokalne.

Def. pochodnej funkcji w punkcie. Pochodną funkcji xo naz. skończoną granicę przy h→0 ilorazu różnicowego i oznaczamy symbolem f ` (xo).f ` (xo)=lim{h→0}(f(xo+h)-f(xo))/h. RYS Równanie stycznej do wykresu y=f(x) w punktach (xo, f(xo)) ma postać y-f(xo)=f ` (xo)(x-xo). Euler: Można wykazać, że ciąg an jest ograniczony i można wykazać, że jest ciągiem rosnącym, czyli jest ciągiem monotonicznym i ograniczonym a więc i zbieżny. Granice tego ciągu oznaczamy „e”. Funkcje cyklometryczne. f(x)=SINX. Df=x∈<−Π/2;Π/2>. Vf=<-1,1>. f jest różnowartościowa w tej Df, a więc istnieje f odwrotna do niej: Vf-1:<-1;1>→<−Π/2;Π/2>. f-1(x)=arcsinx # ∧{x∈<−1;1>} sin(arcsinx)=x # ∧{x∈<−Π/2; Π/2>} arcsin(sinx)=x. f(x)=COSX. Df=<0, Π>. Vf=<−1; 1> # Vf-1:<-1; 1> → <0, Π>.# f-1(x)=arccosx # ∧{x∈<0; Π>} arccos(cosx)=x # ∧{x∈<−1; 1>} cos(arccosx)=x. f(x)=TGX Df=(−Π/2; Π/2) Vf=R Vf-1:R → (−Π/2; Π/2) # f-1(x)=arctgx # ∧{x∈R} tg(arctgx)=x # ∧{x∈(−Π/2; Π/2)} arctg(tgx)=x f(x)=CTGX. Df=(0; Π) Vf=R # Vf-1:R → (0; Π) # f-1(x)=arcctg # ∧{x∈R} ctg(crcctgx)=x # ∧{x∈(0; Π)} arcctg(ctgx)=x

Definicja granicy ciągu liczbowego i jej własności: lim{n→oo} an=a ⇔ ∧{ε>0} ∨{No∈N} ∧{n≥No} |an-a|<ε. Własności: 1) Jeżeli ciąg ma granicę, to ma ją tylko jedną. 2) Jeżeli ciąg {an} ma granicę to każdy podciąg wybrany z tego ciągu ma również taką samą granicę. 3) Każdy ciąg zbieżny jest ograniczony. 4) Każdy ciąg monotoniczny i ograniczony jest zbieżny. Podstawowe własności funkcji. Funkcja jest: 1) rosnąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)<f(x2). 2) niemalejąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)≤f(x2). 3) malejąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)>f(x2). 4) nierosnąca w A⊂Df ⇔ ∧{x1,x2∈A} x1<x2 ⇒ f(x1)≥f(x2). 5) stała w A⊂Df ⇔ ∧{x1,x2∈A} x1≠x2 ⇒ f(x1)=f(x2). 6) parzysta ⇔ ∧{x∈Df} (-x)∈Df ∧ f(-x)=f(x) wykres f parzystej jest symetryczny względem osi y. 7) nieparzysta ⇔ ∧{x∈Df} (-x)∈Df ∧ f(-x)=-f(x) wykres f nieparzystej jest symetryczny względem początku układu współrzędnych. 8) okresowa o okresie podstawowym To(To≠0) ⇔ ∧{x∈Df} (x+To) ∈ Df ∧ f(x+To)=f(x). 9) ograniczona z góry ⇔ ∨{M∈R} ∧{x∈Df} f(x)≤M; ograniczona z dołu ⇔ ∨{M∈R} ∧{x∈Df} f(x)≥M. Funkcja jest ograniczona, gdy jest ograniczona z góry i z dołu. F. odwrotna: def. Niech f: A na→ B. Funkcją odwrotną do funkcji f nazywamy taką funkcję g, która odwzorowuje teraz zbiór B na→ A. ∧{x∈A} ∧{y∈B} y=f(x) ⇔ x=g(y). Tw. Jeżeli f: A na→ B jest różnowartościowa, to istnieje do niej funkcja odwrotna g przeprowadzająca zbiór B na→ A. Symbol: g(x)=f-1(x). Asymptoty wykresu funkcji: 1) Def. Prosta x=a jest asymptotą pionową (lewostronną) wykresu funkcji y=f(x) ⇔ lim{x→a+}{x→a-}f(x)=+-oo. Jeżeli prosta x=a jest asymptotą pionową prawostronną i lewostronną, to nazywany je obustronną. 2) Def. Niech f•x∈(xo, +oo). Prosta y=mx+p jest asymptotą ukośną prawostronną wykresu f: y=f(x) ⇔ lim{x→-oo} [f(x)-(mx+p)]=0. Niech f•x∈(-oo, x1). Prosta y=mx+p jest asymptotą ukośną lewostronną wykresu f: y=f(x) ⇔ lim{x→-oo} [f(x)-(mx+p)]=0. 3) Szczególnym przypadkiem asymptoty ukośnej jest asymptota pozioma. Prosta y=p jest asymptotą poziomą prawostronną (lewostronną) ⇔ lim{x→+oo}{x→-oo} f(x)=p. Twierdzenie: Prosta y=mx+p jest a.ukośną prawostronną (lewostronną) ⇔ 1) lim{x→+oo}{x→-oo} f(x)•1/x=m. 2) lim{x→+oo}{x→-oo} [f(x)-mx]=p Ciągłość funkcji w punkcie i przedziale. A) Def. Funkcja f jest ciągła w punkcie xo ⇔ 1) xo∈Df (jest określona w tym punkcie); 2) lim{x→xo} f(x)=a (ma skończoną granicę); 3) lim{x→xo} f(x)=f(xo) (granica ma taką samą wartość w tym punkcie). xo∈(a,b)∈Df. Definicja odnosi się do punktów nieizolowanych dziedziny. Jeżeli w Df istnieją punkty izolowane Df=(c,d)∪″{xo}″, wtedy w tych punktach z definicji przyjmujemy, że funkcja jest ciągła. Twierdzenia o funkcjach ciągłych: 1) Jeżeli f jest ciągła w <a,b>, to przyjmuje w tym przedziale wszystkie wartości pomiędzy f(a), f(b). 2) Jeżeli f jest ciągła w <a,b>, to przyjmuje w tym przedziale swoją wartość największą i najmniejszą. 3) Jeżeli f jest ciągła w <a,b>, i f(a)-f(b)<0, to ∨{c∈(a,b)} f(c)=0. Def. pochodnej funkcji punkcie. Pochodną funkcji xo naz. skończoną granicę przy h→0 ilorazu różnicowego i oznaczamy symbolem f ` (xo).f ` (xo)=lim{h→0}(f(xo+h)-f(xo))/h. RYS Równanie stycznej do wykresu y=f(x) w punktach (xo, f(xo)) ma postać y-f(xo)=f ` (xo)(x-xo). Reguły różniczkowania. A) (f(x)+g(x)) ` = f ` (x)+g ` (x). B) (α•f(x)) '  = α•f ` (x), α∈R. C) (f(x)•g(x)) ` = f ` (x)•g(x)+f(x)•g ` (x). D) (f(x)/g(x)) ` = (f ` (x)•g(x)-g ` (x)•f(x))/(g(x))2. Tw. Lagrange'a i wnioski: Niech f jest: 1) ciągła w <a,b> 2) różniczkowalna w (a,b) to ∨{c∈(a,b)} f ` (c)=(f(b)-f(a))/(b-a) RYS (f(b)-f(a))/(b-a)=tgβ. Wnioski: 1) Jeżeli funkcja jest różniczkowalna w (a,b) i f ` (x)>0, to funkcja jest rosnąca w (a,b). 2) Jeżeli funkcja jest różniczkowalna w (a,b) i f ` (x)<0, to funkcja jest malejąca w (a,b). 3) Jeżeli funkcja jest różniczkowalna w (a,b) i f ` (x)=0, to funkcja jest stała. 4) Jeżeli funcje f i g są różniczkowalne w (a,b) i w każdym punkcie tego przedziału f ` (x)=g ` (x), to funkcje różnią się tylko o stałą. Wykresy są równoległe: f(x)=g(x)+c w (a,b); c∈R. Ekstrema lokalne i warunek konieczny. Funkcja f(x) ma w punkcie xo (xo∈Df) maksimum lokalne ⇔ ∧{Sxo} ∨{x∈Sxo} f(x) ≤ f(xo). Funkcja f(x) ma w punkcie xo minimum lokalne ⇔ ∧{Sxo} ∨{x∈Sxo} f(x) ≥ f(xo). Jeżeli nierówności występujące w definicji są ostre, to mówimy, że funkcja ma max i min (ekstremum) lokalne właściwe. Tw. Warunek konieczny ekstremum funkcji: Jeżeli funkcja jest różniczkowalna w pewnym otoczeniu punktu xo (Uxo) i ma w xo ekstremum lokalne, to f'(xo)=0. Uwaga: Dla funkcji różniczkowalnych ekstrema lokalne mogą istnieć tylko w punktach zerwania się pierwszej pochodnej. Warunek wystarczający extremum (tw.) Jeżeli funkcja jest różniczkowalna w Uxo oraz: 1) f '(xo)=0; ∧{x∈S-xo} f '(x)>0; ∧{x∈S+xo} f `(x)<0; to f ma w xo minimum lokalne, oraz 2) f `(xo)=0; ∧{x∈S-xo} f '(x)<0; ∧{x∈S+xo} f `(x)>0; to f ma w xo maksimum lokalne. Euler: Można wykazać, że ciąg an jest ograniczony i można wykazać, że jest ciągiem rosnącym, czyli jest ciągiem monotonicznym i ograniczonym a więc i zbieżny. Granice tego ciągu oznaczamy „e”. Funkcje cyklometryczne. f(x)=SINX. Df=x∈<−Π/2;Π/2>. Vf=<-1,1>. f jest różnowartościowa w tej Df, a więc istnieje f odwrotna do niej: Vf-1:<-1;1>→<−Π/2;Π/2>. f-1(x)=arcsinx # ∧{x∈<−1;1>} sin(arcsinx)=x # ∧{x∈<−Π/2; Π/2>} arcsin(sinx)=x. f(x)=COSX. Df=<0, Π>. Vf=<−1; 1> # Vf-1:<-1; 1> → <0, Π>.# f-1(x)=arccosx # ∧{x∈<0; Π>} arccos(cosx)=x # ∧{x∈<−1; 1>} cos(arccosx)=x. f(x)=TGX Df=(−Π/2; Π/2) Vf=R Vf-1:R → (−Π/2; Π/2) # f-1(x)=arctgx # ∧{x∈R} tg(arctgx)=x # ∧{x∈(−Π/2; Π/2)} arctg(tgx)=x f(x)=CTGX. Df=(0; Π) Vf=R # Vf-1:R → (0; Π) # f-1(x)=arcctg # ∧{x∈R} ctg(crcctgx)=x # ∧{x∈(0; Π)} arcctg(ctgx)=x
naႮ x1

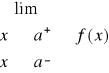
lim{xႮa+}{xႮa-}f(x)

∧∈a⇔∨≤≥°<>•→ε∪⊂⇒≠Π−

---