- przestrzeń probabilistyczna (def. na egzamin!)

- przeliczalny lub skończony

- nieprzeliczalny
inny

Np.: Niech
- przeliczalny
(można ustawić w ciąg)

(
);
;

1)

2)
∅

3)
∅

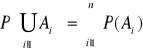
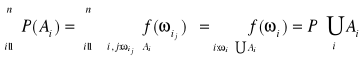
4)

5)

P jest zupełne

Np2: Prawdopodobieństwo klasyczne (wg. Laplace'a)

;

- zdarzenia równoprawdopodobne

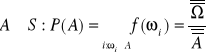
Np3: Rzucamy kostką do gry:

A - parzysta ilość oczek

B - 5 lub 6

(gdy kostka jest symetryczna)

Gdy kostka nie jest symetryczna to musimy zastosować rozkład:

Rzucamy próbnie 100 razy:

	1	2	3	4	5	6
	20	10	15	5	35	15

Np4: Rzucamy monetą tak długo, aż wypadnie dwa razy na tę samą stronę. Jak wygląda przestrzeń zdarzeń elementarnych i jakie jest prawdopodobieństwo, że potrzebna będzie parzysta ilość rzutów.

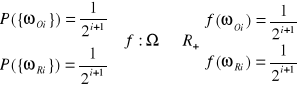
(suma szeregu geometrycznego)

Prawdopodobieństwo warunkowe:

określamy

nowa przestrzeń

jest
ciałem na B

Sprawdzamy, że
jest miarą zupełną i unormowaną na
:

1. 
   

2. 
   ∅
   ∅
   

3. 
   
   

4. 
   ∅
   
   

5. 
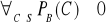
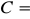
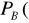
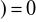
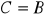
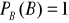
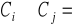
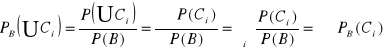
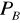
   - zupełne

A zatem
jest miarą zupełną i unormowaną na B, czyli
jest przestrzenią probabilistyczną.

Rozszerzamy miarę
na S

- nowa przestrzeń probabilistyczna

spełnia warunki miary na S (zupełnej i unormowanej)

Załóżmy, że

z założenia
dla

Prawdopodobieństwo całkowite i wzór Bayesa:

1. 
   ∅

2. 
   

3. 
   

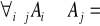
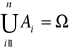
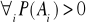
Def: Zdarzenia
spełniające warunki trzy powyższe warunki nazywamy układem zupełnym zdarzeń.

Tw:
;
- przestrzeń zupełna zdarzeń

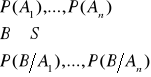
dane

Teza:

Dow:

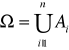
- parami rozłączne

- też rozłączne

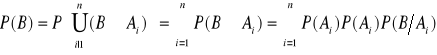
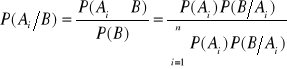
- wzór Bayesa.

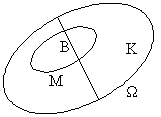
Np.: Na 100 mężczyzn - 5, a na 1000 kobiet - 2 to daltoniści. Z grupy o jednakowej liczbie mężczyzn i kobiet wybrano losowo osobę, która okazała się daltonistą. Jakie jest prawdopodobieństwo, że jest to mężczyzna.

∅

M, K tworzą układ zupełny zdarzeń

B - zbiór wszystkich daltonistów

.

Wieloetapowe doświadczenia losowe:

Np.: Rzucamy monetą 1zł i 2zł

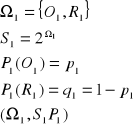
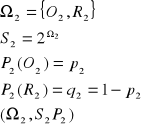
P nazywa się iloczynem kartezjańskim miar
i
. Oznaczamy

Def:
- przeliczalny

- przeliczalny

Tw:

Dla wieloetapowego doświadczenia:

...

...

...

Tw:
, gdzie
(
)

Schemat Bernoulliego:

Rozważamy n identycznych niezależnych doświadczeń losowych, z których każde kończy się jednym z dwóch wyników. Modelem probabilistycznym dla pojedynczego doświadczenia jest:

Doświadczenie łączne polegające na n-krotnym powtórzeniu tego samego doświadczenia opisane jest następująco:

, gdzie

- zdarzenie polegające na tym, że w ciągu
znajdzie się dokładnie
k jedynek

5

Luke Rachunek prawdopodobieństwa-wykład 26.2.2k+1

---