Numer ćwiczenia 308	Data 12XI2012	Imię i Nazwisko Jan Pańka		Wydział BMiZ		Semestr I		Grupa Nr lab.
Prowadzący Dr. Małgorzata Bancewicz			Przygotowanie		Wykonanie		Ocena

Temat: Wyznaczanie współczynnika załamania światła dla cieczy za pomocą refraktometru Abbego.

Podstawy teoretyczne.

Do załamania promienia świetlnego dochodzi na granicy dwóch ośrodków. Kąt zawarty między normalną do powierzchni a kierunkiem promienia nazywamy kątem padania i kątem załamania odpowiednio dla ośrodka pierwszego (przed zetknięciem promienia z granicą) oraz ośrodka drugiego. Ponadto jeśli wiązka przechodzi z ośrodka optycznie rzadszego do ośrodka optycznie gęstszego, to kąt załamania jest mniejszy od kąta padania. W przeciwnym wypadku mamy do czynienia z sytuacją odwrotną - kąt załamania jest większy od kąta padania.

Mimo że każdemu kątowi padania α odpowiada inny kąt załamania β, to wartościami tych kątów rządzi pewne prawo zwane prawem załamania światła (prawem Snella). Wynika z niego, że stosunek sinusów obu kątów jest stały dla danej pary ośrodków i dla danej długości fali światła. Formalnie przedstawia się ono następująco:

,

gdzie n₁ i n₂ są bezwzględnymi współczynnikami załamania światła dla poszczególnego ośrodka. Wielkości te można wyrazić także jako stosunek prędkości światła w próżni c do prędkości światła w danym ośrodku v, zatem:

.

Z powyższej zależności wnioskujemy, że wartość współczynnika zawsze jest większa od jedności, bowiem prędkość światła w próżni jest największa.

Stosunek bezwzględnych współczynników załamania światła obu ośrodków (drugiego do pierwszego) nazywamy względnym współczynnikiem załamania:

.

Bardzo często mamy do czynienia z załamaniem światła na granicy powietrza i cieczy lub ciała stałego. Mając na uwadze prędkość światła w powietrzu bliską jego prędkości w próżni przyjmuje się, że współczynnik załamania dla powietrza wynosi 1. Wobec tego zależność Snella, a więc stosunek sinusów kątów padania i załamania, wyznacza bezwzględny współczynnik załamania ośrodka drugiego (jeśli pierwszym oczywiście było powietrze).

Szczególny aspekt opisywanego zjawiska stanowi całkowite odbicie wewnętrzne, które zachodzi dla kąta większego lub równego tak zwanemu kątowi granicznemu. Dodatkowym warunkiem jest kolejność ośrodków, przez które przechodzi promień. Istotne jest, by pierwszy z nich był optycznie gęstszy od ośrodka drugiego. Wiemy już, że w tym przypadku kąt załamania jest większy od kąta padania. W związku z tym, dla pewnego kąta padania (kąta granicznego α_g), możliwe jest uzyskanie kąta załamania równego 90º. Wówczas promień załamany pokrywa się z linią granicy ośrodków, co innymi słowy oznacza, że nie przechodzi on do ośrodka drugiego. Większe wartości kąta α powodują całkowite odbicie wewnętrzne promienia. Mówimy wtedy wyłącznie o promieniu odbitym jako jedynym powstałym w skutek zetknięcia promienia padającego na granicę ośrodków. Zjawisko ilustruje poniższy rysunek:

Wzór Snella dla kąta granicznego (i wobec powyższego schematu) przyjmuje wygodną postać:

.

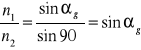
Urządzenia miernicze. Metoda pomiaru.

Aby dokonać odpowiednich pomiarów badanej wielkości, w ćwiczeniu tym należało posłużyć się refraktometrem Abbego. Najważniejszą częścią urządzenia, w której zresztą zachodzi zjawisko załamania światła, są dwa prostokątne pryzmaty P₁ i P₂ ze szkła flintowego o dużym współczynniku załamania. Oba obrócone są względem siebie o 180º wokół prostej, równoległej do dłuższych krawędzi płaszczyzny dłuższej przyprostokątnej każdego z nich i przylegają ściśle płaszczyznami przeciwprostokątnej. Górny pryzmat P₁ może obracać się wokół osi O przechodzącej przez wyżej położoną, krótszą krawędź płaszczyzny przeciwprostokątnej obu pryzmatów, co umożliwia jego odchylanie i nakładanie preparatu na płaszczyznę przeciwprostokątnej pryzmatu drugiego P₂. Po umieszczeniu badanej substancji cieczy na tejże płaszczyźnie, pryzmat P₁ może zostać dociśnięty do pryzmatu P₂, co z kolei utworzy między nimi cienką warstwę ośrodka o mniejszym współczynniku załamania. Padające na pryzmat P₁ światło, a dokładnie na powierzchnię jego krótszej przyprostokątnej, dochodzi pod różnym kątami do płaszczyzny z cieczą. Tam występuje załamanie jego promieni dla kątów mniejszych niż kąt graniczny lub całkowite wewnętrzne odbicie dla większych, bądź równych, i te, które zostaną załamane, przechodzą następnie przez pryzmat P₂, a dalej do lunetki L₁. Pole jej widzenia podzielony jest na dwa obszary: jasny u dołu dla promieni załamanych i ciemny powyżej, gdzie nie dociera światło wskutek całkowitego odbicia. Granica między obszarem jasnym a obszarem ciemnym zależy od współczynnika załamania cieczy, dlatego jej położenie jest różne dla innych wartości tegoż współczynnika. Istotą dokonania pomiaru z użyciem refraktometru jest naprowadzenie ów granicy na środek pola widzenia lunetki L₁ poprzez odpowiedni obrót pryzmatów P₁P₂.

Powyższy rysunek ilustruje treść poprzedniego akapitu. Promienie między 1 i 2 ulegają całkowi-temu odbiciu wewnętrznemu (ciemny obszar widzenia lunetki). Promień 2 pada pod kątem minimalnie mniejszym od kąta granicznego, natomiast wszystkie promienie znajdujące się między 2 a 3 ulegają załamaniu i przechodzą do pryzmatu P₂, a dalej do lunetki L₁ (jasny obszar widzenia lunetki). Granica obu obszarów właściwie naprowadzona jest na środek pola.

Wraz z obrotem pryzmatów P₁ i P₂ sprzężony jest ruch podziałki K, która została skonstruowana zgodnie z zależnością Snella. To umożliwia bezpośredni odczyt współczynnika załamania poprzez lunetkę L₂, która prócz podziałki dla współczynnika załamania zawiera także podziałkę podającą procentową zawartość cukru w roztworze wodnym. W tym ćwiczeniu wykorzystano refraktometr, który w jednej lunetce scala zarówno obraz lunetki L₁, jak i skale lunetki L₂.

Refraktometr uniwersalny, który użyty został w danym ćwiczeniu, umożliwia użycie światła białego, bowiem jego specjalna budowa przeciwdziała pewnemu niepożądanemu dla obserwacji zjawisku. Mianowicie w pryzmatach oraz badanej cieczy dochodzi do zjawiska rozszczepienia światła, tzw. dyspersji. Powoduje to rozmycie granicy między obszarem jasnym i ciemnym w polu widzenia lunetki, która ponadto jest barwna i poprzez to niewyraźna. Do skorygowania tego stanu służy układ dwóch pryzmatów P₃ i P₄, które dodatkowo składają się z pomniejszych, pojedynczych pryzmatów, przeważnie trzech, wykonanych z różnych rodzajów szkła, i różniących się między sobą współczynnikiem załamania. Ich odpowiednie ustawienie względem siebie kompensuje dyspersję wywołaną przez badaną ciecz, dlatego przed właściwym ustawieniem granicy należy poprawić jej wyrazistość odpowiednim pokrętłem.

Na rysunku powyżej przedstawione są wszystkie opisane w tym paragrafie elementy, które składają się na budowę refraktometru Abbego.

Wyniki pomiarów. Wykresy. Niepewności mierzonych wielkości.

Pierwszą częścią zadania było dokonanie pomiarów współczynnika załamania dla wody, a następ-nie pięciu roztworów wodnych gliceryny o różnym stężeniu procentowym przy stałej temperaturze. Każda substancja nakładana była na suchą powierzchnię przeciwprostokątną pryzmatu P₂. Pryzmat P₁ dociskano do pryzmatu P₂ w taki sposób, aby w warstwie cieczy nie pozostawały żadne pęcherzyki powietrza. Po wykonaniu każdego pomiaru przeprowadzano zabiegi mające na celu zapewnić czystość płaszczyzn przeciwprostokątnych obu pryzmatów przed nałożeniem kolejnego preparatu. Odczyt polegał kolejno na skompensowaniu barwnego rozszczepienia światła, naprowadzeniu granicy obszaru jasnego i ciemnego na środek pola widzenia lunetki za pomocą pokrętła pryzmatów P₁P₂ i odczytaniu za pomocą tej samej lunetki współczynnika załamania cieczy na skali poniżej pola widzenia światła. Wyniki otrzymanych z pomiarów wielkości zamieszczono w poniższej tabeli.

Temperatura wszystkich próbek wynosiła 25,0 ºC.

	woda	roztwór wodny gliceryny o różnym stężeniu procentowym
stężenie procentowe roztworu [%]	0	10	30	50	70	100	x
współczynnik załamania n	1,331	1,341	1,368	1,395	1,422	1,468	1,373

Następnie na podstawie pomiarów należało wykonać wykres zależności współczynnika załamania od stężenia roztworu.

Niepewność odczytu współczynnika załamania: Δn = 0,001.

Wnioski.

Po wykonaniu wykresów zauważyliśmy, że nasze pomiary mieszczą się w granicach błędu systematycznego. Na podstawie otrzymanych wyników możemy stwierdzić, że wraz ze wzrostem stężenia roztworu rośnie współczynnik załamania. Wynika to z tego, że w miarę wzrostu stężenia roztwór ma większą gęstość i tym samym zgodnie z prawem załamania wzrasta współczynnik załamania światła. Wyniki pomiarów mogą nie mieścić się w granicach błędu ze względu na to, że podczas przeprowadzania doświadczenia mogliśmy niestarannie oczyścić powierzchnię pryzmatu. Niewiadomy roztwór oznaczony stężeniem „X” odczytaliśmy jego stężenie z tabelki i wynosi 40%

- 5 -

---