WSTĘP TEORETYCZNY

Zmiany temperatury ciała występujące podczas jego ogrzewania lub oziębiania połączone są ze zmianami jego objętości. Zjawisko to, nazwane rozszerzalnością termiczną ciała wiąże się z ich budową kinetyczno - molekularną. Najłatwiej można je wyjaśnić posługując się modelem ciała stałego. Atomy w ciele stałym znajdują się w regularnych odstępach i utrzymywane są siłami pochodzenia elektrycznego. Siły wiążące atomy zachowują się tak, jak siły występujące podczas rozciągania lub zgniatania sprężyny; z tego też względu nazwane siłami sprężystymi. Obrazowo przedstawić je można jako układ sprężyn łączących atomy - ciało stałe wygląda jak rodzaj mikroskopowego materaca. Sprężyny te są bardzo mocne; jest ich około 10²³ w 1cm³. Atomy w ciele stałym drgają w każdej, nawet bardzo niskiej temperaturze. Amplituda tych drgań wynosi około 10^-9 cm, a ich częstość około 10¹³ drgań na sekundę.

Gdy temperatura wzrasta, amplituda drgań atomowych, ogólnie biorąc, wzrasta również; położenie równowagi drgających atomów przesuwają się na nowe, zwiększone odległości. Powoduje to rozszerzenie się ciała stałego. Zmianę liniowych wymiarów ciała stałego, takich jak długość, szerokość czy wysokość, nazywamy rozszerzalnością liniową. Jeżeli ciało w temperaturze początkowej t₀ ma długość początkową l₀, a po ogrzaniu do temperatury t ma długość l_t, to nastąpił przyrost długości Δl=l_t-l₀. Znajdujemy doświadczalnie, że przyrost długości Δl jest proporcjonalny do przyrostu temperatury Δt=t-t₀. Wyrazić to można zależnością :

Δl=αl₀*Δt.

Współczynnik proporcjonalności α nazywamy współczynnikiem rozszerzalności liniowej. Współczynnik ten ma oczywiście różne wartości dla różnych ciał; jest on stałą charakteryzującą rozszerzalność termiczną danej substancji. Jego definicję matematyczną podaje wzór:

.

Liczbowo współczynnik α jest równy przyrostowi jednostki długości pręta ogrzewanego o 1°C. Dokładne pomiary wykazują, że zmienia się om nieco w zależności od tego, w jakim obszarze temperatur pręt jest ogrzewany; np. dla obszaru temperatur 15-30°C współczynnik ten ma inna wartość niż dla zakresu temperatur 25-30°C itd. ściśle mówiąc powyższy wzór oznacza tzw. średni współczynnik rozszerzalności liniowej w obszarze temperatur t_o do t. W większości zagadnień związanych z rozszerzalnością termiczną wystarcz posługiwanie się takim właśnie współczynnikiem. Jednakże w bardzo dokładnych rozważaniach istnieje konieczność posługiwania się współczynnikiem rozszerzalności w danej temperaturze α_t. Taki współczynnik jest średni, współczynnikiem rozszerzalności dla nieskończenie wąskiego zakresu temperatur dt w otoczeniu temperatury t. Określamy go wzorem analogiczny do powyższego, lecz z różniczkowymi przyrostami długości dl i temperatury dt:

Współczynnikiem rozszerzalności objętościowej nazywamy stosunek zmiany objętości ciała do objętości początkowej i zmiany temperatury. Gdy jeden wymiar ciała znacznie przewyższ drugi to nie bada się rozszerzalności objętościowej tylko zajmuje się rozszerzalności liniową (zaniedbujemy rozszerzalność w pozostałych wymiarach)

Dylatometr jest to przyrząd, którym bada się rozszerzalność liniową ciał stałych. Podgrzewa się pręt z danego materiału i obserwuje się czujnik mikrometryczny umieszczony na statywie. Z czujnika określamy przyrost długości. Dodatkowo musimy znać temperaturę np. pary wodnej, temperaturę otoczenia i długość początkową

PRZEBIEG DOŚWIADCZENIA

Na początku kilkakrotnie zmierzyłem długość każdego pręta, miarką milimetrową. Odczytałem też panujące podczas doświadczenia ciśnienie atmosferyczne, oraz temperaturę powietrza. Następnie ogrzałem pręty parą z wrzącej wody i badałem ich wydłużenie za pomocą czujnika mikrometrycznego. Pomiar dla każdego pręta wykonałem dwukrotnie.

OPRACOWANIE WYNIKÓW

Ciśnienie atmosferyczne podczas przeprowadzania doświadczenia wynosiło 757,9mmHg, a temperatura powietrza wynosiła 23°C. Przy taki ciśnieniu woda wrze w temperaturze 99,93°C. Wartość tą odczytałem z tablicy wywieszonej w pomieszczeniu pracowni. Ponieważ temperaturę otoczenia odczytałem z termometru o niedokładności pomiarowej 1°C, to temperaturę wrzenia przybliżam do 100°C. Przy tak danych wartościach i po zamianie stopni celsjusza na kelwiny obliczam temperaturę o jaką podgrzałem pręty i wynosi ona t=77[K].

Poniższa tabela przedstawia pomiary i odpowiednie ich obliczenia.

Pomiar I

NUMER PRĘTA	ŚREDNA DŁUGOŚĆ PRĘTA[mm]	PRZYROST DŁUGOŚCI[mm]	WSPÓŁCZYNNIK ROZSZERZALNOŚCI LINIOWEJ[1/K]
1	756	0,96	1,65*10ˉ^5
2	757	0,68	1,17*10ˉ^5
3	756	1,09	1,88*10ˉ^5
4	757	0,90	1,55*10ˉ^5

Pomiar II

NUMER PRĘTA	ŚREDNIA DŁUGOŚĆ PRĘTA[mm]	PRZYROST DŁUGOŚCI[mm]	WSPÓŁCZYNNIK ROZSZERZALNOŚCI LINIOWEJ[1/K]
1	756	0,97	1,67*10ˉ^5
2	757	0,62	1,07*10ˉ^5
3	756	1,05	1,81*10ˉ^5
4	757	0,94	1,62*10ˉ^5

Średnia wartość wsp. roz. lin. z obu pomiarów

NUMER PRĘTA	WSP.ROZ.LIN. POMIAR I[1/K]	WSP.ROZ.LIN. POMIAR II[1/K]	ŚREDNIA WARTOŚĆ WSP.ROZ.LIN.[1/K]
1	1,66*10ˉ^5	1,67*10ˉ^5	1,67*10ˉ^5
2	1,17*10ˉ^5	1,07*10ˉ^5	1,12*10ˉ^5
3	1,88*10ˉ^5	1,81*10ˉ^5	1,85*10ˉ^5
4	1,55*10ˉ^5	1,62*10ˉ^5	1,59*10ˉ^5

Współczynnik rozszerzalności liniowej liczyłem ze wzoru:

Gdzie: α-współczynnik rozszerzalności linowej

δl-przyrost długości pręta

l₀-długość początkowa pręta

t- temperatura o jaką podgrzano pręt

OCENA BŁĘDÓW

Ponieważ dla każdego pręta przy każdym pomiarze wyszedł mi inny wynik, dlatego też błąd obliczam nie metodą różniczki zupełnej, a metodą średniej kwadratowej.

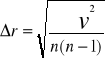
NUMER PRĘTA	BŁĄD POMIARU I	BŁĄD POMIARU II	BŁĄD ŚREDNI
1	0,01 * 10^-5
2	0,04* 10^-5	0,04* 10^-5	0,04* 10^-5
3	0,02* 10^-5	0,03* 10^-5	0,02* 10^-5
4	0,03* 10^-5	0,02* 10^-5	0,02* 10^-5

Ponieważ dla pręta 1 (pomiar II)wartość rozszerzalności liniowej jest taka sama jak wartość średnia z obu pomiarów to dla tego przypadku błąd liczę metodą różniczki zupełnej.

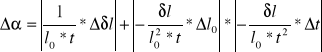
Δα=0,05* 10^-5

A zatem błąd średni dla pomiarów pręta pierwszego wynosi δα=0,03* 10^-5

Przy tak danych błędach pomiarowych wyniki dla poszczególnych prętów przedstawia tabela:

NUMER PRĘTA	WSPÓŁCZYNNIK ROZSZERZALNOŚCI LINIOWEJ[1/K]
1	(1,67 ± 0,03) *10-5
2	(1,12± 0,04) *10^-5
3	(1,85± 0,02) *10^-5
4	(1,59± 0,02) *10^-5

WNIOSKI

Otrzymane wyniki porównałem z danymi zamieszczonymi w Tablicach matematycznych, fizycznych, chemicznych i astronomicznych WSiP Warszawa 1974. Przy uwzględnieniu cech wizualnych (kolor- pręty I oraz III były złotawe, a pręty II i IV były srebrzyste) mogę przypuścić iż:

NUMER PRĘTA	NAZWA MATERIAŁU	WARTOŚĆ WSP.ROZ.LIN. TABLICOWA[1/K]	WARTOŚĆ WSP.ROZ.LIN UZYSKANA[1/K]
1	MIEDZ	1,6	(1,67 ± 0,03) *10-5
2	STAL	1,3	(1,12± 0,04) *10^-5
3	MOSIĄDZ	1,8	(1,85± 0,02) *10^-5
4	STAL NIERDZEWNA	1,6	(1,59± 0,02) *10^-5

Na ewentualne błędy wpływ mógł mieć fakt iż przy drugim badaniu rozszerzalności liniowej danego pręta ich temperatura nie musiała być dokładnie taka sama jak przy pierwszym badaniu (pręty mogły być za zimne lub za gorące).

---