Cel üwiczenia:

Pomiar wydłuĪenia wzglĊdnego drutu w funkcji temperatury oraz wyznaczenie liniowego

współczynnika rozszerzalnoĞci cieplnej.

Zagadnienia:

Oddziaływania miĊdzyatomowe w ciele stałym, zjawisko rozszerzalnoĞci cieplnej, współczynnik

rozszerzalnoĞci termicznej, zasada działania termopary.

Układ i metody pomiarowe:

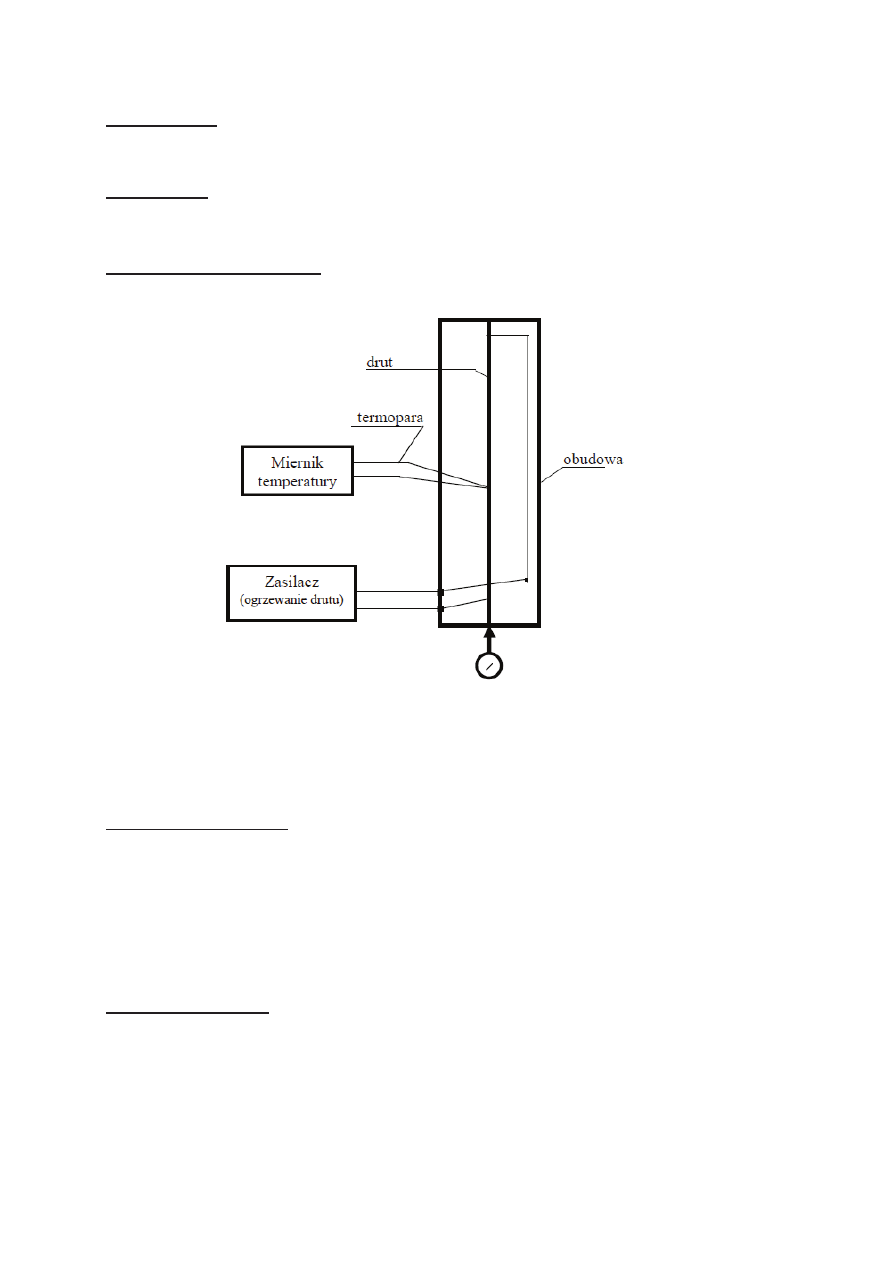
Przy wykonywaniu üwiczenia korzystano z układu pomiarowego:

Rysunek 1. Schemat układu pomiarowego

Zestaw przyrządów, z których korzystano:

•

czujnik mikrometryczny

•

zasilacz prądu stałego

•

cyfrowy miernik temperatury

Zadania do wykonania:

Sporządziü wykres zaleĪnoĞci wzglĊdnego wydłuĪenia drutu ǻL/ L od przyrostu temperatury ǻT

(ǻT=t-t

o

). Dla wybranych punktów z początkowego, Ğrodkowego i koĔcowego zakresu temperatur zaznaczyü

pola niepewnoĞci. Z nachylenia wykresu wyznaczyü współczynnik rozszerzalnoĞci liniowej

D

badanego

materiału.

Metodą regresji liniowej wyznaczyü, a nastĊpnie omówiü, parametry prostej y = Ax±B (gdzie: y =ǻL/Lo

, x=ǻT, A=Į, niepewnoĞü ǻA=ǻĮ ) oraz współczynnik korelacji r. NanieĞü na wykres prostą najlepszego

dopasowania. Porównaü parametry tej prostej z wartoĞcią

D

wyznaczoną w punkcie 1 i przedyskutowaü wnioski

płynące z tych porównaĔ.

Pomiary i obliczenia:

Pomiary zostały dokonane na zestawie nr 2, dla którego L

o

= (0,900 ± 0,004) m. Po wyregulowaniu

zestawu, ustawieniu czujnika mikrometrycznego temperatura początkowa wyniosła 26,5°C. NastĊpnie
ogrzewaliĞmy drut zwiĊkszając wartoĞü prądu przepływającego w obwodzie o ok. 0,4 A. W ten sposób
otrzymaliĞmy 13 pomiarów, zebranych w Tabeli 1.

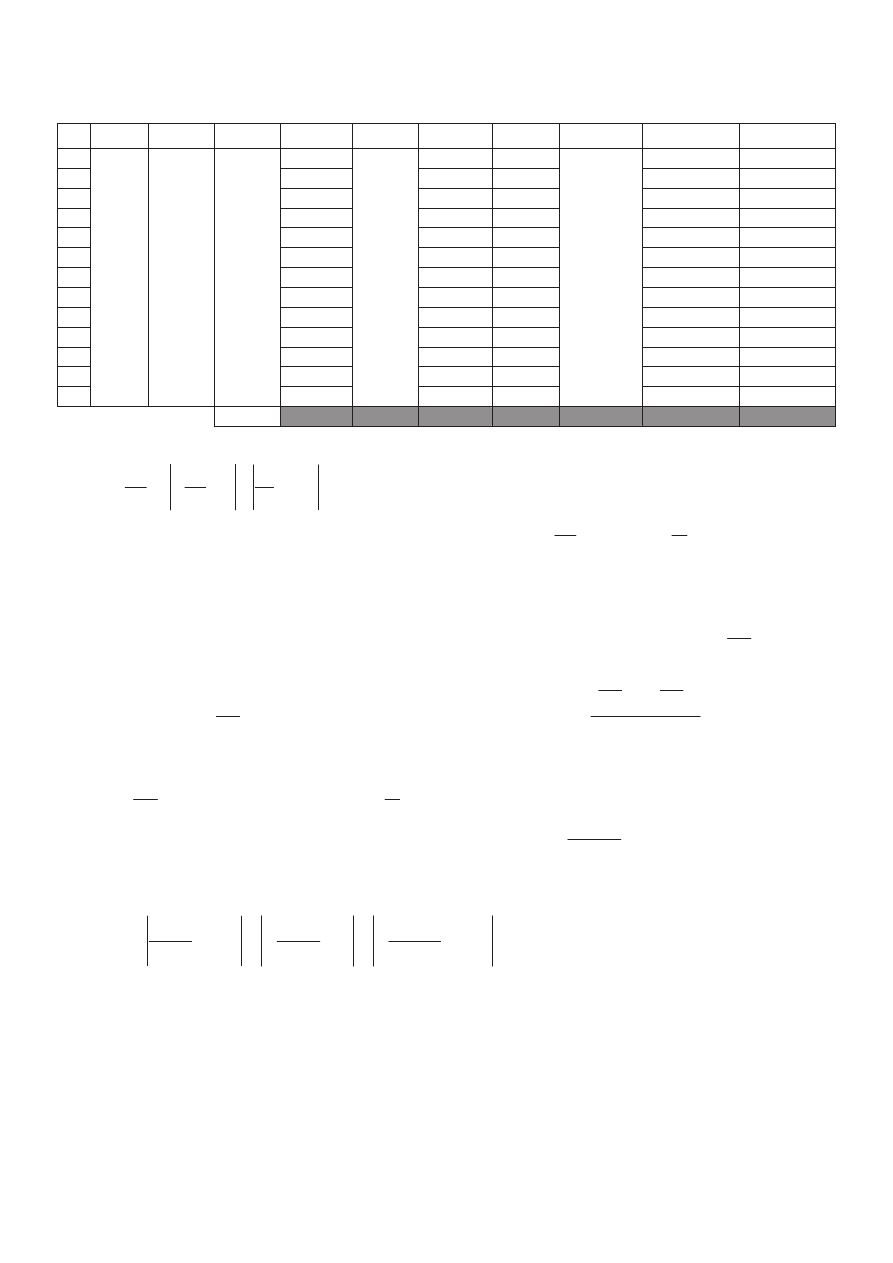
Tabela 1. Pomiary temperatury i obliczenie wzglĊdnego wydłuĪenia druta

Lp. L

0

[mm] ǻLo[mm]

to[

o

C]

t[

o

C]

ǻt[

o

C]

ǻT[

o

C]

ǻL[mm] ǻ(ǻL)[mm]

ǻL/L

0

ǻ(ǻL/L0)

1

28,9

2,4

0,04

0,000044

0,000011

2

37,2

10,7

0,16

0,000178

0,000012

3

48,5

22,0

0,32

0,000356

0,000013

4

57,4

30,9

0,46

0,000511

0,000013

5

92,3

65,8

0,95

0,001056

0,000016

6

99,3

72,8

1,06

0,001178

0,000016

7

111,6

85,1

1,22

0,001356

0,000017

8

118,3

91,8

1,35

0,001500

0,000018

9

127,0

100,5

1,46

0,001622

0,000018

10

133,6

107,1

1,62

0,001800

0,000019

11

142,2

115,7

1,77

0,001967

0,000020

12

153,0

126,5

2,00

0,002222

0,000021

13

900

4

26,5

156,2

1

129,7

2,15

0,01

0,002389

0,000022

ĝrednie:

100,4

1

73,9

1,12

0,01

0,001244

0,0000166

NiepewnoĞü wzglĊdnego wydłuĪenia druta liczymy metodą róĪniczki zupełnej.

)

(

1

)

(

0

0

2

0

L

L

L

L

L

L

L

o

∆

∆

+

∆

∆

−

=

∆

∆

Po podstawieniu danych i uĞrednieniu wyników otrzymujemy

K

L

L

1

0000166

,

0

)

(

0

≈

∆

∆

.

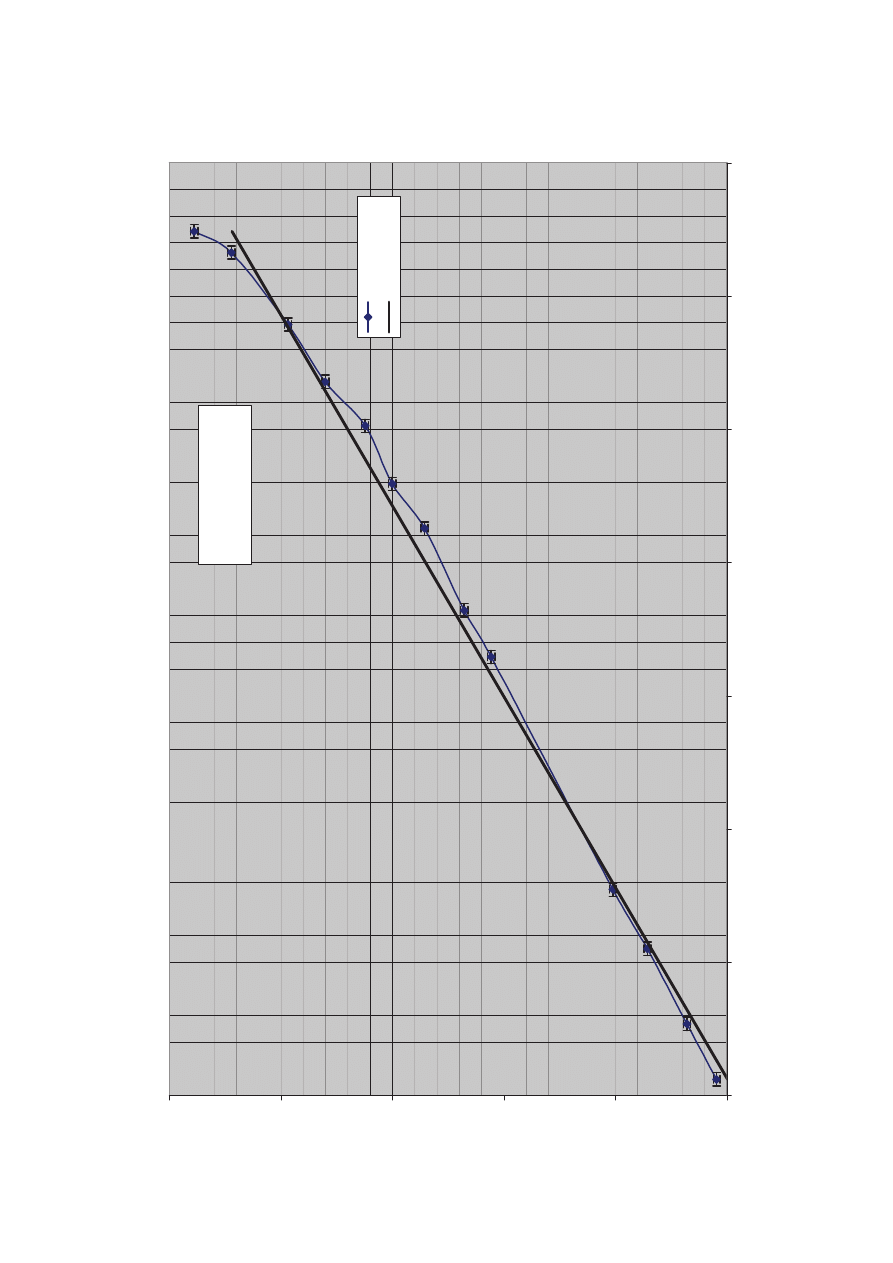
Na podstawie Tabeli 1 moĪemy sporządziü wykres zaleĪnoĞci wzglĊdnego wydłuĪenia druta od

przyrostu temperatury. Wykres wykonany w MS Excel znajduje siĊ w dalszej czĊĞci sprawozdania. Na
podstawie wykresu moĪemy obliczyü współczynnik rozszerzalnoĞci liniowej

D

materiału, z którego wykonany

jest drut. W tym celu wybieramy punkty z wykresu, które nie są punktami pomiarowymi np.

o

L

L

∆

1

=19,

T

∆

1

=112 oraz

o

L

L

∆

2

=0,

T

∆

2

=0 i korzystamy z zaleĪnoĞci

2

1

2

0

1

0

)

(

)

(

)

(

)

(

T

T

L

L

L

L

tg

a

∆

−

∆

∆

−

∆

=

=

α

. Dodatkowo

zamieniamy tu jednostkĊ, w której bĊdziemy podawaü temperaturĊ, ze stopni Celsjusza na Kelwiny, aby wynik
był zgodny z definicją współczynnika.

K

a

1

10

17

,

0

10

169642857

,

0

112

19

4

4

−

−

×

≈

×

=

=

Definicja współczynnika rozszerzalnoĞci cieplnej brzmi

)

(

0

0

0

t

t

l

l

l

k

k

−

−

=

α

i jest to odpowiednio

przekształcony wzór z którego juĪ korzystaliĞmy. Skorzystamy z metody róĪniczki zupełnej, aby policzyü
niepewnoĞü współczynnika rozszerzalnoĞci cieplnej. Licząc pochodne cząstkowe po kaĪdej zmiennej i
podstawiając za róĪniczki niepewnoĞci wielkoĞci pomiaru otrzymujemy:

)

(

)

(

1

2

0

2

0

0

T

T

L

L

L

T

L

L

L

T

L

u

o

a

∆

∆

∆

∆

−

+

∆

∆

∆

−

+

∆

∆

∆

=

WĞród danych które do tej pory wyliczyliĞmy nie ma niepewnoĞci ǻT. Aby ją wyliczyü ponownie

skorzystamy z róĪniczki zupełnej, zamiast róĪniczek podstawiamy wartoĞci niepewnoĞci. Po wykonaniu tych
czynnoĞci otrzymujemy niepewnoĞü pomiaru przyrostu:

0

)

(

t

t

k

T

∆

−

∆

=

∆

∆

.

Jako Īe pomiar temperatury wykonaliĞmy tym samym przyrządem, pomiar długoĞci początkowej i

koĔcowej jest obarczony taką samą niepewnoĞcią. Wykorzystując ten fakt moĪemy zmodyfikowaü wzór i
doprowadziü go do postaci:

t

T

∆

=

∆

∆

2

)

(

Do obliczeĔ za ǻL i ǻT przyjĊliĞmy Ğrednie arytmetyczne. Podstawiając wartoĞci liczbowe do

wyprowadzonego wzoru otrzymujemy:

07

-

778313E

6,80580538

07

-

282636E

4,55454962

08

-

929253E

7,48191826

07

-

802752E

1,50306393

2

9

,

73

900

12

,

1

4

9

,

73

900

12

,

1

01

,

0

9

,

73

900

1

2

2

=

+

+

=

⋅

⋅

+

⋅

⋅

+

⋅

⋅

=

a

u

MetodĊ regresji liniowej wykorzystują róĪne programy m. in. program Regresja.pas, z którego

korzystałam przy wyznaczaniu prostej regresji. Wyliczony programem współczynnik oraz jego niepewnoĞü
wyniosły: A=(0,00001747±0,00000048) 1/K. Obliczenia zostały wykonane na poziomie ufnoĞci równym
238,265.

PowyĪsze obliczenia zostały zebrane dla przejrzystoĞci w postaci tabeli:

Tabela 2. Zestawienie wyników

Į(z wykresu)[1/K]

A[1/K]

ǻĮ[1/K]

ǻA[1/K]

ǻĮ/Į[%]

ǻA/A[%]

0,00001696

0,00001747

0,00000069

0,00000048

4,07

2,75

Wnioski koĔcowe

Z pomiarów jak i wykresu wynika, iĪ przyrost długoĞci druta jest proporcjonalny do przyrostu

temperatury. Mówi o tym wzglĊdnie wysoki współczynnik korelacji liniowej, który wyniósł 99,18%. Przy
odpowiednich zaokrągleniach wartoĞü współczynnika rozszerzalnoĞci temperaturowej wyznaczona dwoma
metodami była by równa sobie. RóĪnice pojawiają siĊ dopiero w niepewnoĞci współczynnika rozszerzalnoĞci
cieplnej. Przy czym obliczenia wykonane w programie Regresja.pas są dokładniejsze. Wynika to z przybliĪenia
jakie zastosowano w ǻ(ǻT). Fakt ten wpłynął równieĪ na wielkoĞü błĊdu wzglĊdnego. W metodzie gdzie
zastosowano przybliĪenie jest on wiĊkszy.

Mimo to istnieją mocne podstawy, aby sądziü, Īe współczynnik jest wyznaczony poprawnie.

Porównując otrzymane dane z tabelami rozszerzalnoĞci temperaturowej moĪna spróbowaü okreĞliü z jakiego
materiału został wykonany badany drut. Otrzymane wyniki wskazują, Īe była to miedĨ lub jakiĞ jej stop.

W

y

k

re

s

1

.

Z

a

le

Ī

n

o

Ğ

ü

i

w

z

g

lĊ

d

n

e

g

o

w

y

d

łu

Ī

e

n

ia

p

rĊ

tu

o

d

z

m

ia

n

y

t

e

m

p

e

ra

tr

y

y

=

0

,1

7

4

7

x

-

0

,4

6

9

8

R

2

=

0

,9

9

1

8

0

5

1

0

1

5

2

0

2

5

0

,0

2

0

,0

4

0

,0

6

0

,0

8

0

,0

1

0

0

,0

1

2

0

,0

1

4

0

,0

ǻ

T

ǻ

L

/L

0

[x

1

0

-4

]

ǻ

L

/L

0

L

in

io

w

y

(

ǻ

L

/L

0

)

T