Akademia Techniczno Rolnicza w Bydgoszczy
Wydział Mechaniczny
Zakład Ogólnych Podstaw Konstrukcji Maszyn
Studium : mgr Skład grupy:
Semestr IV 1. Tomasz Jagła
Grupa A 2. Paweł Frankowski
Zespół ćw. B 3. Robert Gugała
Data ćw. 14.04.1999 4. Adam Sagan
5. Ireneusz Olszak
T : Badanie strat tarcia w łożysku ślizgowym.
1)Wprowadzenie
podział łożysk ślizgowych
-ze względu na prędkość obwodową v:
1) Poza chwilami rozruchu i zatrzymania maszyny v=const, zatrzymywanie maszyny rzadkie
2) v zmienne co do wartości i ewentualnie co do kierunku
3) wartości i kierunek v periodycznie zmienne, ruch obrotowy oscylacyjny
-ze względu na obciążenie:
obciążenie P=const, co do wartości i co do kierunku (łożyska obciążone statycznie)
wartość P=const, a kierunek zmienny, wartość P zmienna, a kierunek stały, wartość i kierunek P zmienne (łożysko obciążone dynamicznie)
-ze względu na rodzaj tarcia na powierzchniach ślizgowych:
1) z tarciem suchym lub mieszanym
z tarciem płynnym
--ze względu na kierunek obciążenia w stosunku do osi wału:
1) łożyska poprzeczne
łożyska wzdłużne
łożyska poprzeczno - wzdłużne
b) własności użytkowe łożysk ślizgowych
- obciążalność łożyska
- odporność na zużycie
- odporność na zatarcie
- zdolność do dotarcia
- zdolność do współpracy z olejem zanieczyszczonym
- wytrzymałość zmęczeniowa
- odporność na korozję
- odkształcalność (zdolność do współpracy z wałem o osi nierównoległej do osi panwi)
- zdolność do chwilowej pracy bez smarowania
- odporność na kawitację
c) metody badań łożysk ślizgowych
- pomiar strat energetycznych
- badania trwałości
- badania i pomiar procesów temperaturowych i cieplnych
- na etapie wykonania:
- kontrola wymiarów i stanu powierzchni
- metody badań nieniszczące
- metody badań niszczące
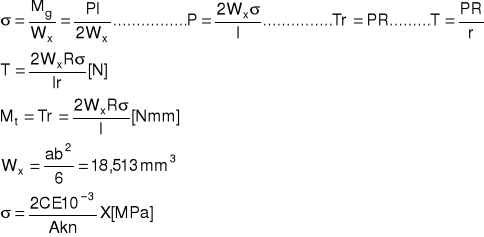
2)Pomiar strat energetycznych w łożyskach ślizgowych
W grupie pomiarów strat energetycznych w łożyskach ślizgowych mieści się badanie oraz pomiar strat tarcia. Cechą zasadniczą tych pomiarów jest określenie momentu oporu tarcia Mt przy uwzględnieniu siły tarcia T oraz ramienia działania tej siły rt wg wzoru Mt = Trt
Pomiaru strat tarcia w łożyskach ślizgowych dokonujemy w dwojaki sposób:
- poprzez wprowadzenie zależności stałej prędkości i obciążeń wzrastających lub malejących
- poprzez wprowadzenie zależności stałego obciążenia i zmiennej prędkości obrotowej
3)Hydrodynamiczna teoria smarowania
Z równania Reynoldsa wynika, że ciśnienie p w warstwie smaru jest odwrotnie proporcjonalne do kwadratu luzu łożyskowego, a wprost proporcjonalne do lepkości smaru i prędkości kątowej czopa.Wyrażenie:
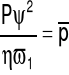
jest charakterystycznym parametrem łożyska, zwanym bezwymiarowym wyróżnikiem ciśnienia.
![]()
Na Rys.1. została wyznaczona siła reakcji (nośność) W warstwy smaru. Następnie rozłożono tę siłę na dwie wzajemnie prostopadłe składowe wzdłuż osi X i Y prostokątnego układu współrzędnych.
Na podstawie rysunku można zauważyć, że kąt ϕ , określający miejsce położenia najmniejszej wysokości hmin warstwy smaru względem obciążenia wyraża się zależnością:
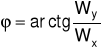
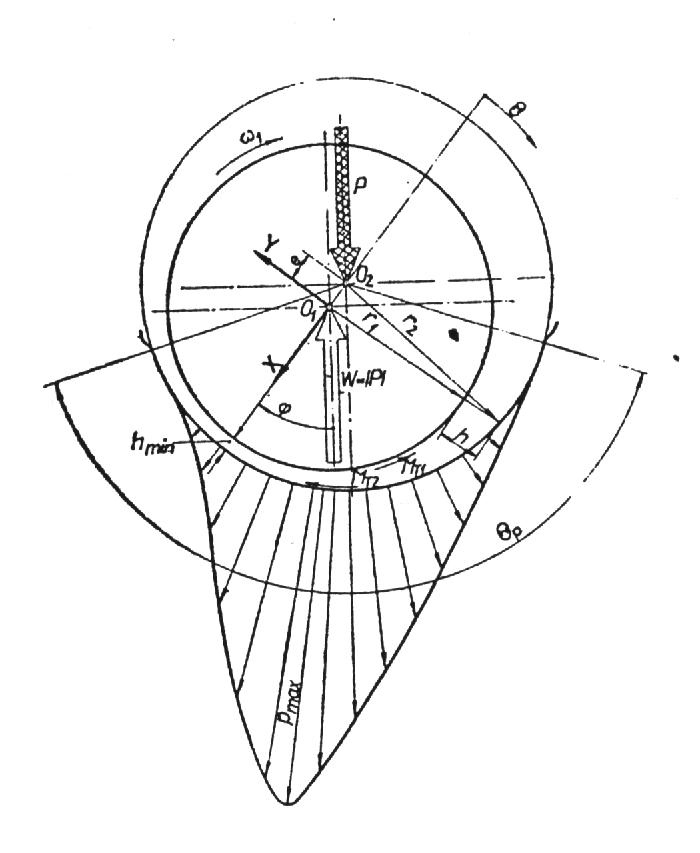
Rys.1. Zależności geometryczne w poprzecznym łożysku ślizgowym przy tarciu płynnym
oraz rozkład ciśnienia hydrodynamicznego wzdłuż obwodu panwi.
Wskutek mimośrodowości położenia środków czopa i panwi moment tarcia na powierzchni panwi nie jest równy momentowi tarcia na powierzchni czopa. Zgodnie z Rys.1. linia działania obciążenia P przechodzi przez środek panwi, natomiast kierunek siły reakcji W przechodzi przez środek czopa. W przeciwnym kierunku niż kierunek prędkości kątowej ϖ1 działa na czop moment tarcia MT1. Na podstawie warunku rwnowagi można obliczyć moment tarcia MT2 na powierzchni panwi:
![]()
Z powyższego równania wynika, że moment tarcia na powierzchni panwi jest mniejszy niż na powierzchni czopa. O stratach energetycznych decyduje najczęściej moment MT1, działający na czop, który jest napędzanym.
Współczynnik tarcia na powierzchni czopa :
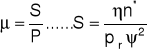

4) Zakres bezpiecznej pracy łożyska ślizgowego
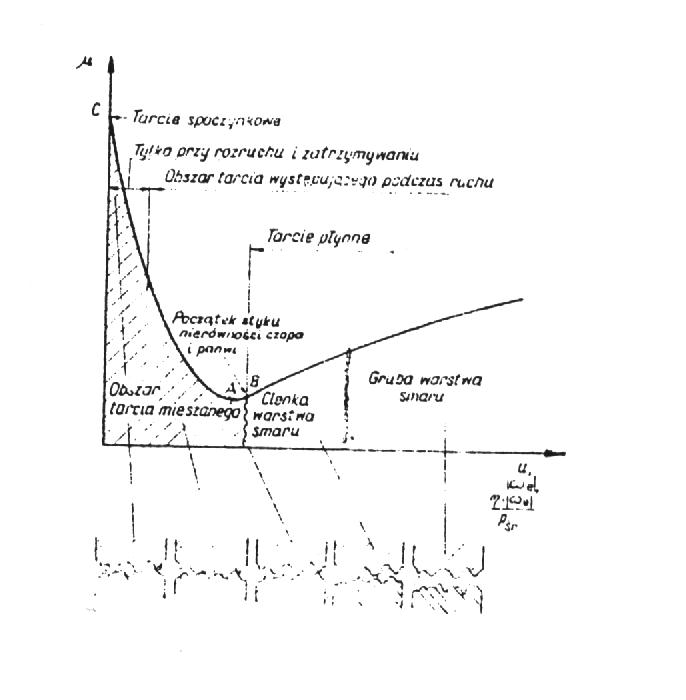
Rys.2. Zmiany współczynnika tarcia w łożysku ślizgowym.
W chwili rozruchu współczynnik tarcia jest duży. Ze wzrostem prędkości obrotowej przy stałym obciążeniu współczynnik tarcia maleje, osiągając w punkcie A mnimum, a następnie wzrasta, co uwarunkowane jest lepkością (tarciem wewnętrznym) smaru. Wzrost współczynnika tarcia po przekroczeniu punktu A jest tym większy, im większa jest lepkość smaru oraz im mniejszy jest względny luz łożyskowy.
Punkt A odpowiada teoretycznemu przejściu z obszaru tarcia mieszanego do obszaru tarcia płynnego. W rzeczywistości jednak, ze względu na chropowatość współpracujących powierzchni oraz sztywności podparcia panwi, przejście to rozpoczyna się w pewnej odległości w prawo od punktu A (w punkcie B). Dokładne ustalenie położenia punktu B w stosunku do A nie jest możliwe, dlatego nie ma dotychczas jednoznacznego kryterium przejścia tarcia mieszanego w tarcie płynne. Na szczególną uwagę zasługuje kryterium krytycznej prędkości obrotowej nk .Jest to najmniejsza prędkość obrotowa przy której w łożysku obciążonym siłą o stałej wartości może istnieć tarcie płynne. Prędkość ta określona jest wzorem:
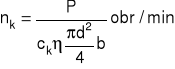

Łożysko, którego punkt pracy leży na prawej gałęzi krzywej Rys.2. jest w stanie trwałej równowagi termicznej. Jeśli z jakiegokolwiek powodu (np. przeciążenia) nastąpi zwiększenie tarcia w łożysku, spowoduje to wzrost jego temperatury, który z kolei przyczyni się do spadku lepkości smaru, a w związku z tym także współczynnika tarcia. Zmniejszenie współczynnika tarcia wpłynie na obniżenie temperatury i powrót do pierwotnych warunków pracy (zjawisko samoregulacji warunków pracy łożyska).
5)Opis ćwiczenia
1) Obiekt badań: łożysko ślizgowe z panewką wykonaną z brązu
2) Zakres ćwiczenia
a) badanie strat tarcia występującego w łożysku ślizgowym
b) określenie zakresu bezpiecznej pracy łożyska
Rys.3. Schemat wyjaśniający sposób pomiaru strat tarcia 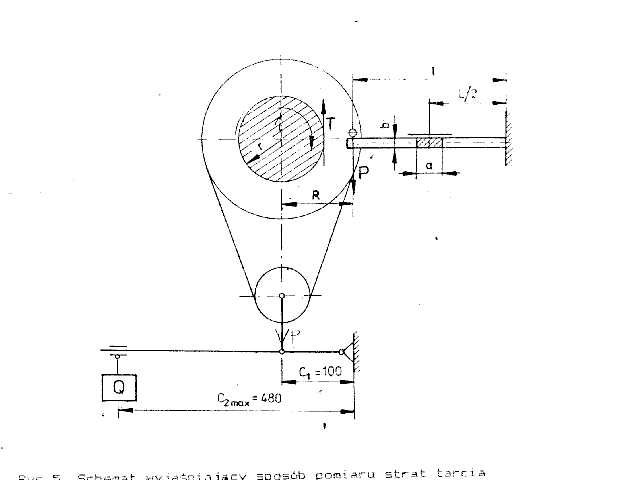
6)Obliczenia
E=210000 MPa
k - stała tensometru = 2,15
C - czułość mostka tensometrycznego = 0,5
A - kalibracja = 38 mm
n=1
x - zapis [mm]
l = 69 mm a = 10,2 mm b = 3,3 mm R = 48 mm r = 17 mm
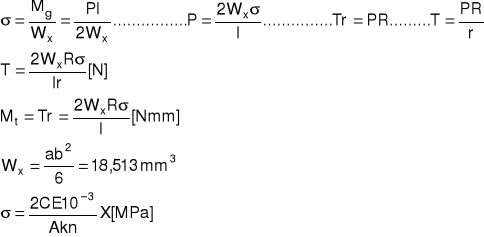
Naprężenia gnące w sprężynie:
7)Wyniki pomiarów
n=const. = 300 obr/min
Q (kG) |
x (mm) |
σ (MPa) |
Mt (Nmm) |
0 |
8 |
20,6 |
529,6 |
2 |
15 |
38,6 |
993 |
4 |
16,5 |
42,4 |
1092,4 |
6 |
20 |
51,4 |
1324,1 |
8 |
22,5 |
57,8 |
1489,6 |
10 |
25 |
64,3 |
1655,1 |
Q=const. = 10 kG
n (obr/min) |
x (mm) |
σ (MPa) |
Mt (Nmm) |
0 |
42 |
107,6 |
2780,6 |
40 |
20 |
51,4 |
1324,0 |
60 |
18 |
46,3 |
1191,7 |
80 |
22 |
56,5 |
1456,5 |
100 |
24 |
61,7 |
1588,9 |
150 |
26 |
66,8 |
1721,3 |
200 |
28 |
72,0 |
1853,7 |
260 |
30 |
77,1 |
1986,1 |
300 |
31 |
79,7 |
2052,3 |
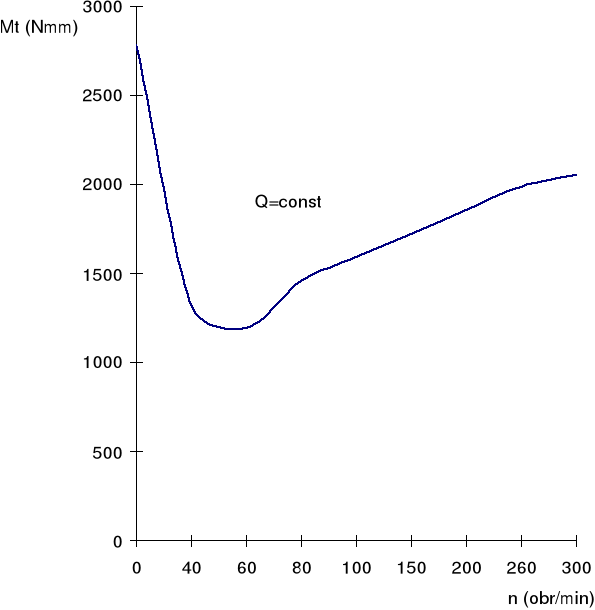
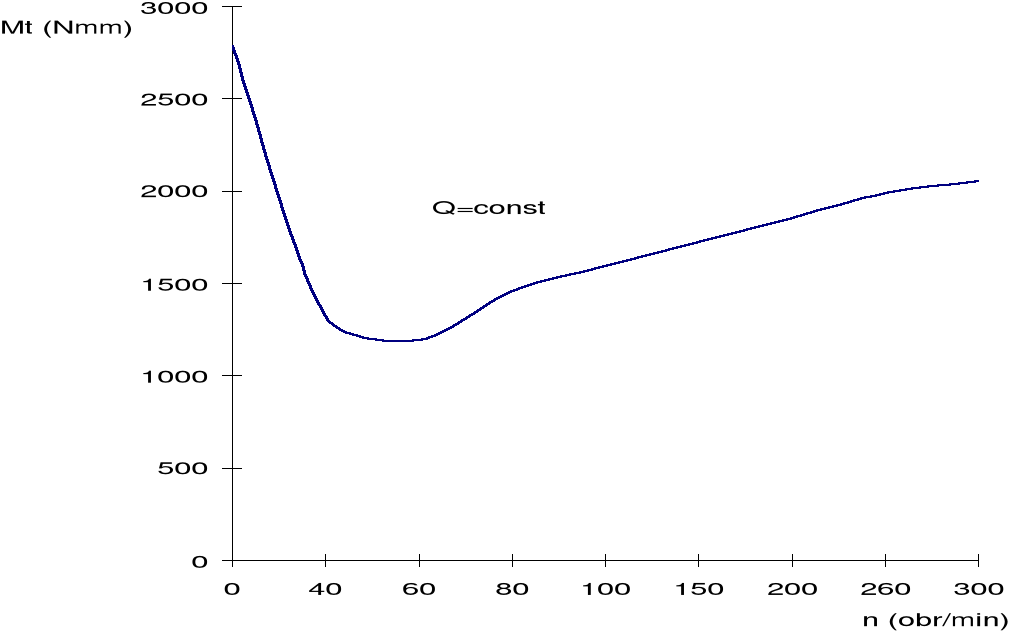
Rys.4. Zależność momentu tarcia od obrotów, przy stałym obciążeniu.
7)Uwagi i wnioski
Wyniki pomiarów potwierdzają teorię łożysk ślizgowych. Przy zmiennych obrotach moment tarcia osiągnął maksymalną wartość, gdy obroty wynosiły zero, a więc w łożysku występowało tarcie spoczynkowe. Następnie moment tarcia zmniejszał swoją wartość w obszarze tarcia mieszanego aż osiągnął minimalną wartość. Prędkość obrotowa wynosiła dla minimalnego momentu około nk=60 obr/min. Ta trudna do dokładnego określenia prędkość krytyczna określa punkt przejścia łożyska z tarcia mieszanego w tarcie płynne, w obszarze którego moment tarcia rośnie.
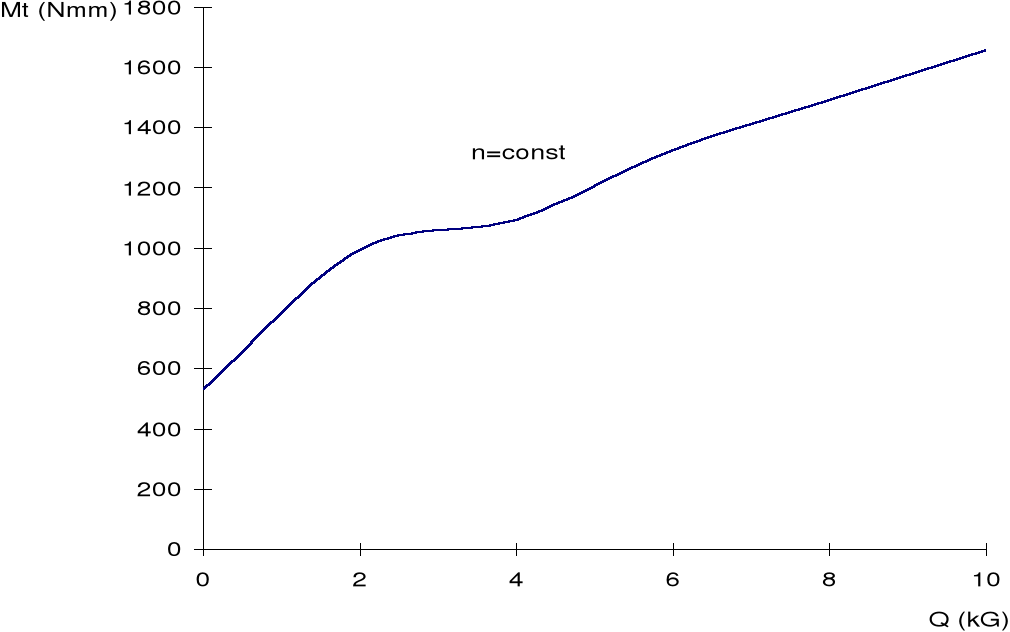
Na Rys.5. otrzymaliśmy wykres momentu tarcia przy zmieniającym się obciążeniu i stałej prędkości obrotowej. Dla obciążenia równego zero otrzymaliśmy pewną wartość momentu tarcia, wynikającą m.in. z ciężaru samej belki. Ciężar belki można wyznaczyć z zależności:
![]()
gdzie T wyliczamy dla σ, odpowiadającego zerowemu obciążeniu.
Następnie obserwujemy wzrost momentu tarcia i chwilową stabilizację w małym przedziale obciążenia, a potem ciągły wzrost aż do maksymalnego obciążenia.
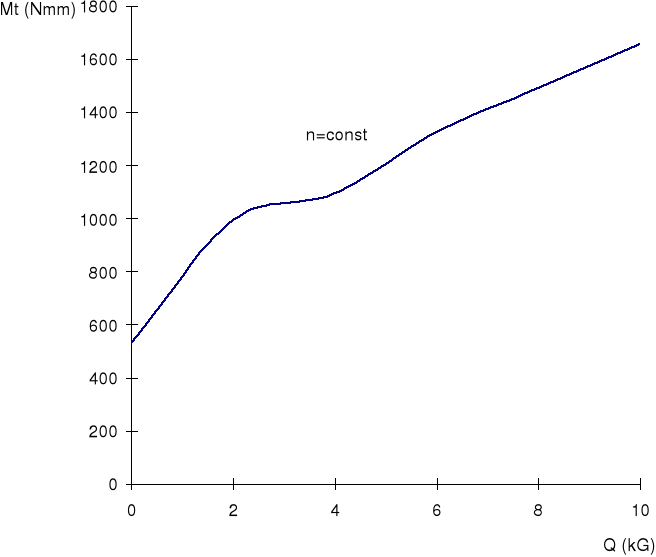
Rys.5. Zależność momentu tarcia od obciążenia, przy stałych obrotach.
7
![]()
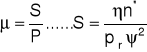

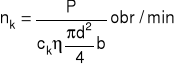

![]()
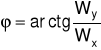
![]()
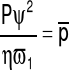
Wyszukiwarka
Podobne podstrony:
pkm lozyska sciaga, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem 4 l
Badanie efektywnosci pracy hamulca tasmowego1, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UT
ścinanie, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem 4 laborka
Naprężenie tnące w spoinach pachwinowych, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, lab
laborka pkm, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem 4 laborka
PKM przekładnia pasowa, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem
SPR, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem 4 laborka
pkm przekladnia sciaga, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem
PKM sprzęgła, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem 4 laborka
teczka, AGH-IMiR-AiR, IV semestr, Podstawy Konstrukcji Maszyn, Inne
Dopuszczalne naciski powierzchniowe, AGH-IMiR-AiR, IV semestr, Podstawy Konstrukcji Maszyn, Inne
PKM projekt, Lotnictwo i Kosmonautyka WAT, semestr 3, Podstawy konstrukcji maszyn, Projekt przekładn
PKM - opracowania roznych pytan na egzamin 6, Automatyka i Robotyka, Semestr 4, Podstawy konstrukcji
projekt dla rudego, Automatyka i Robotyka, Semestr 4, Podstawy konstrukcji maszyn, Projekt
egzam - 3 zadania, Studia, samestr IV, PKM2, Podstawy konstrukcji maszyn II, Egzaminy
Pytania 2, Automatyka i Robotyka, Semestr 4, Podstawy konstrukcji maszyn, Pytania i pomoce
PKM pytania-krzych, Automatyka i Robotyka, Semestr 4, Podstawy konstrukcji maszyn, Teoria
Ściąga PKM(1), Automatyka i Robotyka, Semestr 4, Podstawy konstrukcji maszyn, Teoria, PKM
więcej podobnych podstron