Temat: Ruch cząstki wzdłuż prostej - przejście do przypadku ciągłego

Wyprowadzenie równania Schrödingera w reprezentacji położeń

Rys. 12.1

Niech
będzie amplitudą prawdopodobieństwa znalezienia cząstki w i-tym segmencie łańcucha w chwili t. Dla zbioru amplitud, który możemy nazwać funkcją falową dyskretnego argumentu, wprowadziliśmy specjalne oznaczenie

.

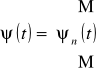
Ponieważ cząstka nie może opuścić łańcucha amplitudy te spełniają warunek normowania, zapiszemy go w reprezentacji położeń

.

Przyjmijmy, że w momencie czasu t cząstka jest zlokalizowana, tj. znajduje się w n-tym segmencie łańcucha. Ponieważ cząstka przeskakuje z węzła na węzeł, więc amplituda musi “rozpływać” się. Niech
będzie amplitudą przejścia z n-tego do
-go przedziału w ciągu jednostkowego interwału czasu. Ta wielkość jest związana ze współczynnikiem A obec­nym w równaniach (12.2) określającym przejścia do sąsiednich węzłów. Niech w momencie czasu t cząstka znajduje się w
-tym segmencie Amplituda prawdopodobieństwa znalezienia tej cząstki w późniejszym momencie czasu
w n-tym segmencie jest proporcjonalna do długości interwału
i amplitudy
w momencie czasu t

.

Podobnie w najniższym przybliżeniu (
) jest amplitudą prawdopodobieństwa znalezienia cząstki w n-tym segmencie w momencie czasu (
) jeżeli w jeżeli w chwili t znajdowała się ona w sąsiednim segmencie
. Amplitudy
ma wymiar odwrotności czasu.

Rozpatrzymy równanie bilansu dla amplitudy
. Dla dostatecznie krótkiego interwału czasu, w pierwszym przybliżeniu należy uwzględnić “wyciekanie” amplitud prawdopodobieństwa do sąsiednich segmentów i “wciekanie” nich do rozważanego segmentu. Zatem

. (13.1)

Drugi i trzeci wyraz sumy znajdującej się po prawej stronie równania (13.1) określa “wciekanie” amplitudy prawdopodobieństwa do n-tego segmentu, natomiast ostatni wyraz jej “wyciekanie” z niego.

W granicy
równanie (13.1) prowadzi do równania różniczkowego zwyczajnego dla amplitudy

. (13.2a)

Względem zmiennej przestrzennej jest to równanie różnicowe. Można je zapisać w postaci macierzowej

, (13.2b)

gdzie

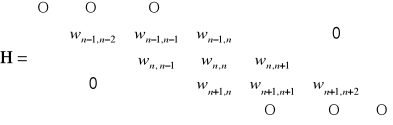
. (13.3)

By macierz H była hermitowska muszą być spełnione następujące warunki

,
,
. (13.4a,b,c)

Równaniu (13.2a) dla amplitud odpowiada równanie dla wektora stanu

. (13.5)

Naszym celem jest znalezienie postaci tego operatora w granicy
. Za Baymem [1] przyjmiemy następującą postać współczynników diagonalnych w_nn

, (13.6)

wtedy równanie (13.2a) przyjmuje postać

. (13.7a)

Moduł kwadratu amplitudy
jest prawdopodobieństwem znalezienia cząstki w n-tym segmencie łańcucha w chwili t. Zatem gdy długość segmentu łańcucha b dąży do zera, wtedy
dąży do amplitudy prawdopodobieństwa
, gdzie
jest gęstością am­plitudy prawdopodobieństwa. Kwadrat modułu amplitudy
jest gęstością prawdopodo­bieństwa znalezienia cząstki w punkcie
prostej, a więc
jest odpo­wiednim prawdopodobieństwem.

Powrócimy do równania Schrödingera (13.7), które granicy
staje się równaniem dla gęstości amplitud prawdopodobieństwa. W tej granicy mamy do czynienia ze zbiorem amplitud
(x₁ może być równe
, a x₂ -
) tworzących funkcję falową
, która zależy od dwóch zmiennych - czasu t i współrzędnej x. Dlatego zamienimy pochodną zwyczajną
obecną w równaniu różniczkowym zwyczajnym (13.2a), a różnicowym względem zmiennej przestrzennej, na pochodną cząstkową

. (13.7b)

Rozłożymy gęstości amplitud
w szeregi potęgowe w b

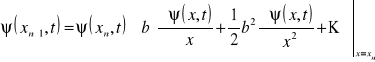
. (13.8)

Wypiszemy wyrazy znajdujące się po prawej stronie równania (13.9)

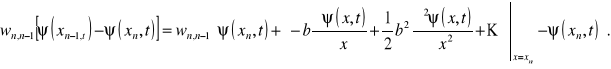
Podobnie

.

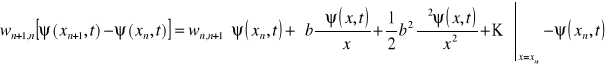
Z dokładnością do wyrazów kwadratowych w b dwa pierwsze wyrażenia stojące po prawej stronie równania (13.8) przyjmują postać

.

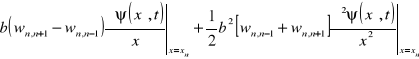
Możemy już napisać przekształcone równanie Schrödingera

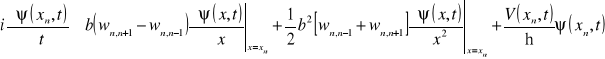
. (13.7c)

Lecz amplituda przejścia
także zależy od b. Wprowadzimy oznaczenia
. Jest to amplituda przeskoku w prawo, natomiast
jest amplitudą przeskoku w lewo. Ze wzoru (13.4b) po sprzęgnięciu obydwu stron i przesunięciu ich argumentów o (-b) wynika związek

. (13.8a)

Podobnie wzór (13.4c) można zapisać w postaci
. W najniższym przybliżeniu względem b

. (13.8b)

Podstawimy amplitudy w_L, w_R w najniższym przybliżeniu do równania (13.7c) i ograniczymy się do wyrazów co najwyżej kwadratowych w b

.

Gdy na układ nie działają siły zewnętrzne amplituda przejścia w lewo nie powinna różnić się od amplitudy przejścia w prawo

. (13.8c)

Na mocy warunku (13.4) stwierdzamy, że amplituda prawdopodobieństwa w jest wielkością rzeczywistą w^* = w. Na podstawie definicji (12.16) stwierdzamy, że
powinna być wielkością skończoną proporcjonalną do
, zatem

, (13.10)

skąd znajdujemy postać równania Schrödingera w granicy

. (13.11)

Wielkość
będziemy utożsamiać z niejednorodnym przestrzenie, zależnym od czasu potencjałem. Ponieważ mamy do czynienia z ruchem cząstki wzdłuż prostej, a nie w sieci nie ma powodu by współczynnik m^* różnił od masy m cząstki w próżni, dlatego położymy

.

Wyjaśnimy sens przejścia granicznego
. Wartość bezwzględna odwrotności amplitudy przejścia określa charakterystyczny czas przeskoku
(por. § 12.4). Widzimy więc, że
. Gdy
to czas przeskoku rośnie nieograniczenie (
), a więc amplituda prawdopodobieństwa nie “wycieka” i nie “wcieka”. Jak widać tak się dzieje w granicy klasycznej. Im cięższa cząstka, tym jest dłuższy czas “przeskoku”. Przebycie drogi o długości b wymaga czasu
. Jest to zależność charakteryzująca dyfuzję - w naszym przypadku dyfuzję prawdopodobieństwa. Jednak, w odróżnieniu od zwykłych równań dyfuzji masy, energii itd., „współczynnik” dyfuzji gęstości amplitudy prawdopodobieństwa
jest wielkością urojoną.

Uogólnimy otrzymane równanie na przypadek ruchu cząstki w przestrzeni. Gęstość amplitudy prawdopodobieństwa
i potencjał
zależą od wektora wodzącego r punktu przestrzeni. Drugą pochodną cząstkową
obecną w równaniu (13.11) należy zamienić na laplasjan

.

Równanie Schrödingera dla funkcji falowej cząstki poruszającej się w przestrzeni ma postać

. (13.12)

13.2 Ruch cząstki swobodnej

Przypuśćmy, że potencjał V nie zależy od czasu. Rozpatrzymy ruch cząstki swobodnej, na którą nie wpływają pola zewnętrzne. To oznacza, że potencjał znika we wszystkich punktach obszaru
, w którym znajduje się cząstka:

. Wtedy

. (13.13)

Wzorując się na rozwiązaniu w postaci (12.10) przyjmiemy, że

. (13.14)

Po obliczeniu pochodnych po czasie i po zmiennych przestrzennych z równania (13.13) wynika, że energia E zależy od pędu p w sposób charakterystyczny dla cząstki swobodnej

. (13.15)

Ponieważ
, gęstość prawdopodobieństwa nie zależy od zmiennych przestrzennych i czasu. W każdym momencie czasu jest ona jednakowa w każdym punkcie obszaru
. Możemy więc powiedzieć, że w każdym momencie czasu cząstka nie jest zlokalizowana.

13.3 Reprezentacja położeń

Przyjmijmy, że cząstka może się znajdować w punktach całej przestrzeni R³. Przestrzeń trójwymiarowa R³ jest iloczynem kartezjańskim trzech przestrzeni jednowymiarowych. Zatem wektor
jest iloczynem tensorowym trzech wektorów

. (13.16)

Ponieważ zbiór wektorów
tworzy zupełny zbiór, a każda ze składowych wektora położenia r przyjmuje wartości z przedziału
więc

. (13.17)

Rozpatrzymy iloczyn dwóch wektorów
i
. Wstawimy między te wektory operator (13.17)

. (13.18)

Ponieważ wektory stanu są unormowane do jedności więc gdy
to ze wzoru (13.18a) wynika, że

,

Jest to oczywisty warunek, który powinna spełniać funkcja rozkładu prawdopodobieństwa. Zasada superpozycji w reprezentacji położeń przyjmuje postać

.

Ta postać mówi, że gdy cząstka znajduje się w dowolnym stanie
to na ogół istnieje nieznikające prawdo­po­dobieństwo zdarzenia polegającego na tym, że będzie się zachowywała ona jak gdyby znajdowała się w dowolnym stanie
.

Rozpatrzymy amplitudę
. Wstawimy pomiędzy składniki tego iloczynu jedynkę operatorową (13.17), otrzymamy

. (13.19a)

Jak widać iloczyn skalarny
równy jest dystrybucji delta
wprowadzonej przez Paula Diraca

. (13.19b)

Przypomnijmy najważniejsze własności tej dystrybucji. Z postaci (13.16) wektora stanu
wynika, że

. (13.20a)

Niech
będzie dowolną funkcją różniczkowalną wszędzie dowolną liczbę razy, wtedy

. (13.30b)

W szczególności gdy
, to

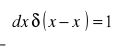
. (13.20b)

Ponieważ amplituda
jest rzeczywista więc
, zatem dystrybucja delta jest funkcja parzystą

. (13.20c)

Rozpatrzymy całkę dystrybucji

.

To oznacza, że

. (13.20d)

Ze względu na parzystość dystrybucji delta we wzorze (13.20d) obecna jest wartość bez­względna parametru a. Dystrybucję delta definiują ciągi. Podajmy postać elementu najbardziej znanego z nich

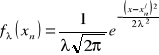
. (13.21)

Ciąg (13.21) dąży dystrybucji delta
gdy
.

Rozpatrzymy szczególny wybór wektora stanu (13.19a), niech
wtedy
. Gęstość prawdopodobieństwa zdarzenia polegającego na tym, że cząstka będąca w stanie
(tj. znajdująca się w punkcie r₀ przestrzeni R³) znajdzie się w stanie
(tj. w punkcie r przestrzeni R³) jest równa

. (13.22)

Ta funkcja nie jest unormowana do jedności, co więcej jej całka nie istnieje. Ta trudność wynika z użycia wektorów stanu i funkcji falowych cząstki doskonale zlokalizowanej. Pokażemy dalej, że z zasady nieoznaczoności Heisenberga wynika, że pęd takiej cząstki jest zupełnie nie określony, a więc i jej energia nie jest określona. Obydwie te wielkości mogą być dowolnie duże, a więc używanie doskonale zlokalizowanych stanów jest niefizyczne i nie­fizyczna jest postać gęstości prawdopodobieństwa (13.22).

Wprowadzimy operator położenia cząstki
. Jest to operator wektorowy
, którego wektorami własnymi są wektory położeń

. (13.23)

Gdy cząstka może znajdować się w każdym punkcie przestrzeni R³ wartości własne składowych wektora położeń spełniają nierówności
. Stwierdzamy więc, że w tym przypadku widmo operatora położenia jest ciągłe i nieograniczone. Zbadajmy jak działa operator składowej położenia na wektory stanu. W tym celu rozpatrzymy wektor
i wstawimy operator
(13.17)

.

Jak widać otrzymaliśmy spektralną postać α-tej składowej operatora położenia

. (13.24)

Rozpatrzymy element macierzowy
, jak zawsze wstawimy w odpowiednie miejsce operator (13.17)

.

Gdy
to

. (13.25)

Jak widać w reprezentacji położeń operator α-tej składowej położenia jest diagonalny, bo czynnik
nie znika wtedy i tylko wtedy gdy
. Jednocześnie czynnik ten wskazuje “miejsce” elementu macierzowego w nieskończonej “macierzy” parametryzowanej ciągłym parametrem. Elementy tej “macierzy” są składowymi wektora wodzącego cząstki. Zbadajmy jeszcze element macierzowy potencjału
. Gdy operatorową funkcję
można rozłożyć w szereg potęgowy to

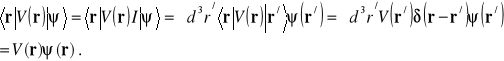
(13.26)

By uniknąć paradoksów należy zażądać by funkcja operatorowa
była jednoznaczna [2].

Będziemy uważali wzór (13.26) uważali za definicję elementu macierzowego potencjału.

13.4 Dyfuzja cząstek wzdłuż prostej

Rozpatrzymy zagadnienie dyfuzji cząstek na prostej [3] Załóżmy, że cząstki poruszają się wzdłuż węzłów łańcucha. Odległość pomiędzy sąsiednimi węzłami wynosi b. Co interwał czasu τ każda z nich skacze do lewego albo prawego sąsiedniego, najbliższego węzła z prawdopodobieństwem
(Rys. 12.2)

Rys. 12.3

Niech
będzie liczbą cząstek w węźle j
po wykonaniu n
- kroków. Liczby te spełniają równanie bilansu

Założymy, że
i wprowadzimy dwie zmienne kwziciągłe: czas
i odległość
. Niech każda z cząstek ma masę m. W granicy
gęstość masy
spełnia równanie dyfuzji

, (13.27)

gdzie κ jest współczynnikiem dyfuzji

. (13.28)

Aby w granicy
współczynnik dyfuzji nie znikał
.

Literatura:

[1] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading, Mass., 1974, R. 3.

[2] B.W. Miedwiediew, Naczała teoreticzeskoj fiziki, Nauka Moskwa, 1977, R. 3, § 5.

[3] Ja. B. Zeldowicz, A.D. Myszkis, Elementy matematiczeskoj fiziki, sreda iz niewzaimodejstwujuszczich czastic, Nauka, Moskwa, 1973, R. 5.

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

n

(n+1)

(n-1)

b

x

---