Podstawowe zasady wyrównania

Rozważmy doświadczenie, w którym przeprowadzono wielokrotne pomiary tej samej wielkości. Ze zbioru n wartości
, i = 1,...,n określających wartości szukanej wielkości chcemy wyznaczyć wartość najlepszą tj. najbardziej prawdopodobną zbliżoną maksymalnie do wartości prawdziwej. Zbiór metod prowadzących do tego celu, to rachunek wyrównawczy, a uzyskanie tej najbardziej prawdopodobnej wielkości to proces wyrównania.

Wiemy, że wynik eksperymentu zawiera błędy pomiarowe, które podlegają prawu rozkładu normalnego. Zatem, aby uzyskać wartość prawdziwą każdy wynik pomiaru trzeba poddać drobnym korektom tj. poprawkom, których wartości uzyskuje się w procesie wyrównania. Wyrównanie wyników pomiaru nieznanej wielkości będzie, zatem polegać na algebraicznym dodaniu do poszczególnych spostrzeżeń drobnych, wyznaczonych w optymalny sposób poprawek. Najlepszymi poprawkami byłyby błędy prawdziwe spostrzeżeń, lecz w praktyce trudno je wyznaczyć, dlatego korzysta się tutaj z błędów pozornych. W tym przypadku spełnione są równania

dla i = 1, 2, ... ,n

Poprawki
, które z konieczności zastępują tu błędy prawdziwe muszą być odpowiednio wybrane, ponieważ istnieje nieskończenie wiele układów poprawek spełniających powyższe związki. Istnieją rózne kryteria wyboru poprawek, jednakże za najlepsze uznaje się kryterium Legendre`a (1805 r.) nazywane "zasadą wyrównania układów obserwacyjnych wg metody najmniejszych sum kwadratów poprawek", tj.

W przypadku, gdy wyniki pomiarów posiadają różne dokładności, co uwzględniamy wprowadzając pojęcie wag
powyższy związek ma ogólniejszą postać:

Naczelną zasadą wyrównania jest, więc rozwiązanie zagadnienia metodą najmniejszych kwadratów tzn. trzeba tak dobrać parametry funkcji, żeby był spełniony warunek

Praktycznie rozwiązanie polega na przyrównaniu do zera pochodnych cząstkowych i rozwiązanie otrzymanego układu równań, nazywanego normalnym lub transformacją Gaussa. Oznacza to taki dobór parametrów krzywej F(t), dla której suma kwadratów odległości rzędnych punktów krzywej od odpowiednich rzędnych obserwacji osiąga wartość najmniejszą.

Realizację wyrównania według zasady najmniejszych kwadratów można przeprowadzić następującymi metodami: spostrzeżeń bezpośrednich, pośredniczącą i zawarunkowaną. Metoda spostrzeżeń bezpośrednich jest szczególnym przypadkiem metody pośredniczącej (dla jednej zmiennej). Wybór metody wyrównania jest głównie uzależniony od nakładu prac przygotowawczych i obliczeniowych. Szczegółowiej zaprezentujemy wyrównanie spostrzeżeń bezpośrednich, a przybliżone sposoby wyrównania układów wyników pomiarów podamy przy omawianiu poszczególnych konstrukcji wyznaczających położenie punktów w przyjętym układzie współrzędnych.

Wyrównanie spostrzeżeń jednej zmiennej

Dla wyznaczenia wartości tej samej wielkości fizycznej x dokonaliśmy bezpośredniego n-krotnego pomiaru tej wielkości, otrzymując szereg na ogół różnych wartości
, i = 1,...,n. Zakłada się, że każda z tych wartości obarczona jest błędem przypadkowym (
). Sama czynność wyrównania polega tu na algebraicznym dodawaniu do wyników pomiaru
małych wielkości zwanych poprawkami
, dobranymi dla poszczególnych spostrzeżeń, tak, aby były one najbardziej prawdopodobne:

Korzystając z warunku Legendre`a otrzymujemy funkcję

,

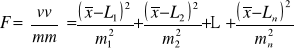
dla której mamy znaleźć minimum, przy wyrównaniu spostrzeżeń o różnej dokładności. (Wyrównanie spostrzeżeń jednakowo dokładnych potraktujemy jako przypadek szczególny).

Wykorzystując pojęcie wagi określonej wzorem

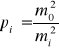
po przyjęciu m0 = 1 funkcja F przyjmuje postać

Jej pochodna wyraża się wzorem

Przyrównując ją do zera otrzymujemy wyrażenie

,

które w skróconym zapisie ma postać

Stąd najbardziej prawdopodobną (wyrównaną w sensie metody najmniejszych kwadratów) wartością x, jest

Wartość wyrównaną nazywa się średnią wagową albo średnią arytmetyczną ogólną. Łatwo zauważyć, że jeżeli
, to wzór przybiera postać wzoru na zwykłą średnią arytmetyczną.

Ocena błędu wartości wyrównanej

Uzyskana w toku wyrównania niewiadoma x jako średnia arytmetyczna ważona, jest obarczona również błędem, który nazywamy błędem wartości wyrównanej. Błąd średniej arytmetycznej można wyznaczyć z prawa przenoszenia się błędów, ponieważ jest ona liniową funkcją pomiarów bezpośrednich
:

Stosując to prawo otrzymamy

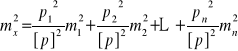
Wyrażając kwadraty błędów średnich przez wagi

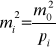
i podstawiając je do powyższej zależności otrzymamy:

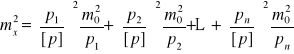
Po uproszczeniu otrzymamy:

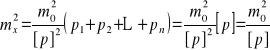
lub

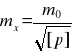
Wzór ten jest równoważny następującej zależności

,

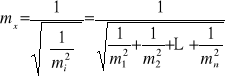
która nie wymaga wprowadzenia pojęcia wag.

Dla spostrzeżeń jednakowo dokładnych wzór ten przyjmuje postać

Obliczanie błędu średniego pojedynczego pomiaru

Na podstawie użytych do wyrównania spostrzeżeń należy ocenić ich błąd średni, stanowiący miarę dokładności każdego spostrzeżenia. Błąd ten, zwany błędem średnim pojedynczego spostrzeżenia lub błędem przed wyrównaniem, określa się przy użyciu błędów pozornych, uzyskanych w wyniku metody wyrównania.

(Wyznaczenie wartości takiego błędu bezpośrednio na podstawie błędów prawdziwych
.

zwykle nie jest niemożliwe, ponieważ nie znamy błędów prawdziwych. )

W metodzie najmniejszych kwadratów [vv] jest mniejsza od [εε], co do której uczyniliśmy założenie, że musi spełniać warunek minimum, zaś [ε], o ile jest wyliczalna, takich założeń nie wymaga. Ponieważ

lub

Po podniesieniu do kwadratu i zsumowaniu otrzymamy

.

Przyrównując pochodną do zera mamy

.

Stąd

W równaniu różnica
nie jest znana. Zależność między wielkością najbardziej prawdopodobną a prawdziwą określona jest wzorem:

Na tej podstawie równość [] można zapisać w postaci

lub

Korzystając z definicji błędu średniego

równość
przyjmie postać:

Po przeniesieniu i wyciągnięciu przed nawias kwadratu błędu średniego otrzyma się ostateczną odpowiedź:

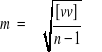
Oznacza to, że błąd średni pojedynczego spostrzeżenia równy jest pierwiastkowi z sumy kwadratów poprawek (błędów pozornych), podzielonemu przez ilość spostrzeżeń nadliczbowych. Różnica n-1 oznaczająca ilość spostrzeżeń nadliczbowych w statystyce nazywa się ilością punktów (stopni) swobody, bowiem dla jednoznacznego określenia pojedynczej wielkości konieczne jest tylko jedno spostrzeżenie, zaś pozostałe stanowią materiał nadliczbowy. Znaczy to też, że określając ilość koniecznych spostrzeżeń, równą k, otrzymamy wzór ogólnej postaci:

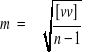
Przy wyrównaniu spostrzeżeń o różnej dokładności otrzymujemy poprawki do spostrzeżeń pomierzonych, których odpowiednie błędy średnie wynoszą m1, m2, ... , mn.

Wiedząc, że

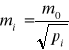
otrzymamy wzór:

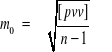
dla jednej zmiennej, lub wzór

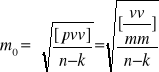
dla k zmiennych.

Powyższe związki prowadzą do bezpośredniego otrzymania wzoru na wartość błędu średniej arytmetycznej dla spostrzeżeń jednakowo dokładnych

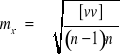
Natomiast dla spostrzeżeń niejednakowo dokładnych będzie

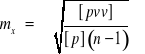
Dla pełnej analizy dokładności opracowanych wyników pomiarów należy jeszcze powiedzieć, jaką wagę posiada wartość wyrównana.

Waga średniej arytmetycznej ze spostrzeżeń wyrównanych o różnej dokładności równa się sumie wag, zaś dla spostrzeżeń jednakowej dokładności waga równa się ilości spostrzeżeń, z których obliczono średnią.

Przykład 1. Obliczyć najprawdopodobniejszą wartość azymutu boku poligonowego, średni błąd typowego spostrzeżenia oraz średni błąd wyrównanej wartości, mając trzy wyniki na azymut tego boku, otrzymane z trzech ciągów poligonowych
o ilości wierzchołków odpowiednio

Wyniki obliczonych azymutów boku 1-2 oraz przebieg wyrównania podano w tabeli:

Nr	Spostrzeżenia li	Wagi pi	v	pv	pvv
1	120g30c 95cc	1,25	-34	-42,50	1445,00
2	120g30c55cc	0,50	6	3,00	18,00
3	120g 30c10cc	0,77	51	39,27	2002,77
	Suma	2.52	23	-0,23	3465,77

Ponieważ przy obliczeniu każdego z trzech azymutów boku brały udział wszystkie kąty każdego ciągu poligonowego, wobec tego dokładność (a więc i waga) obliczonego azymutu boku będzie zależna od ilości kątów, których użyto do obliczenia azymutu. Innymi słowy, waga każdego z tych trzech spostrzeżeń będzie odwrotnie proporcjonalna do ilości kątów:

W celu uproszczenia dalszych obliczeń wszystkie wagi pomnożono przez 10.

Obliczenia:

,

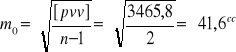
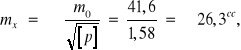
Przykład. 2. Pomierzono wielokrotnie odcinek AB, przy czym do pomiaru użyto trzech różnych taśm. Wyniki zestawiono w poniższej tabeli. Należy obliczyć najprawdopodobniejszą wartość pomierzonego odcinka i jego średni błąd. Kolejność rozwiązania:

1. obliczenie średniej arytmetycznej spostrzeżeń dla każdej taśmy i jej średniego błędu;

Nr	Taśma 20 m	Taśma 50 m	Ruletka 25 m
1	245,50	245,53	245,58
2	245,56	245,58	245,56
3	245,57	245,50	245,58
4	245,60	245,59	245,56
5	245,52
6	245,49

Taśma 20 m:










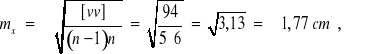
Taśma 50 m:










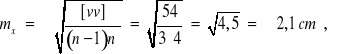
Ruletka 25 m:










2. obliczenie średniej arytmetycznej ogólnej z poszczególnych trzech średnich arytmetycznych wymienionych w punkcie a).

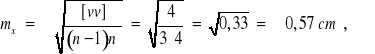
Przebieg wyrównania przedstawia tabela:

Nr	Spostrzeżenia [m]	mx [cm]	p	v [cm]	pv	pvv
1	245,540	1,8	1,0	2,6	2,6	6,76
2	245,550	2,1	0,8	1,6	1.3	2,08
3	245,570	0,6	9,0	-0,4	-3,6	1,44
			10,8		0,3	10,28










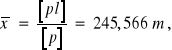
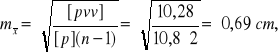
Wyrównanie spostrzeżeń parami

Dwa bezpośrednie spostrzeżenia odnoszące się do jednej wielkości nazywa się parą spostrzeżeń. W praktyce geodezyjnej dość często stosuje się pomiar parami, np. dwukrotny pomiar boków, kątów w dwóch położeniach lunety, wyznaczanie różnic wysokości ciągami niwelacyjnymi w obu kierunkach itd. Obliczanie średniego błędu dla jednej pary obserwacji jest oczywiście możliwe, ale ze względu na zbyt małą ilość obserwacji (n = 2) do uzyskanego wyniku nie można mieć dużego zaufania. Biorąc to pod uwagę, zagadnienie wyrównania spostrzeżeń parami musi być traktowane jako zagadnienie kompleksowe, dotyczące szeregu par tych samych spostrzeżeń lub tego samego rodzaju wielkości. Ocena dokładności pomiaru kątów w danej sieci poligonowej, na podstawie uzyskanych różnic d z dwóch położeń lunety może służyć jako przykład, w którym należy zastosować wyrównanie spostrzeżeń parami. Gdyby obserwacje nie były obciążone żadnymi błędami przypadkowymi i systematycznymi, wtedy różnica pomiarów tej samej wielkości równałaby się zeru. Nieuniknione błędy przypadkowe (i część błędów systematycznych) obarczają jednak wyniki pomiarów i stąd występujące różnice d można uważać za błędy prawdziwe.

Oznaczając wyniki pomiarów pewnego szeregu wielkości l1, l2,...,ln odpowiednio przez
,
, ... ,
można utworzyć następujące różnice:


,
, ...,
.

Można, więc napisać wzór na błąd średni poszczególnej różnicy


.

Z drugiej strony jeżeli wyniki wszystkich pomiarów uznaje się za jednakowo dokładne, to na podstawie prawa przenoszenia błędów dla każdej pary pomiarów można napisać


.

Z powyższych zależności wynika następujący wzór na błąd średni pojedynczego pomiaru
:


.

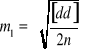
Korzystając z tego wzoru dla n = 2 można określić średni błąd średniej arytmetycznej każdej dowolnej pary spostrzeżeń:


.

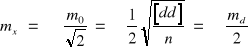
Gdy parom spostrzeżeń odpowiadają różne wagi, wtedy błąd średni md różnicy spostrzeżeń określamy wzorem


.

Z uwagi na jednakową dokładność obu spostrzeżeń jednej pary, wzór wyrażający średni błąd pojedynczej obserwacji (o wadze 1) jest następujący:


.

Średni błąd średniej arytmetycznej dwóch pomiarów oblicza się na podstawie zależności




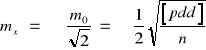
Należy zachować jednolity sposób obliczania różnic
tzn. dla wszystkich par należy odejmować wynik drugiego pomiaru od pierwszego lub dla wszystkich par zastosować odwrotną kolejność odejmowania.

Podane wzory są słuszne tylko wtedy, gdy różnice par spostrzeżeń mają charakter błędów przypadkowych. Oznaką występowania błędów systematycznych jest zdecydowana przewaga wartości różnic dodatnich nad ujemnymi lub odwrotnie. W takim przypadku, w celu uwolnienia poszczególnych różnic od wpływu błędu systematycznego σ, należy obliczyć jego wartość, jako średnią arytmetyczną wszystkich n różnic:


(is)

W przypadku różnic jednakowo dokładnych, należy odjąć błąd systematyczny σ od każdej różnicy i w ten sposób obliczyć poprawione różnice d, czyli




Gdy poszczególne różnice mają różną dokładność, obliczony według wzoru (is) błąd systematyczny σ jest błędem systematycznym jednostkowym
(
). Przyjmuje się wtedy, że wpływ błędu systematycznego na poszczególne różnice
jest proporcjonalny do odwrotności wag
.

Posługujemy się, zatem wzorami




gdzie


.

W przypadku różnic jednakowo dokładnych, należy odjąć błąd systematyczny σ od każdej różnicy i w ten sposób obliczyć poprawione różnice d, czyli




Gdy poszczególne różnice mają różną dokładność, wpływ błędu systematycznego na poszczególne różnice
jest proporcjonalny do odwrotności wag
().

Posługujemy się, zatem wzorami




oraz




Skorygowane różnice d w obu podanych przypadkach tracą swój charakter błędów prawdziwych, a nabierają cech błędów przypadkowych i w związku z tym odpowiednio zmieniają się wzory na obliczenie błędów średnich. Dla różnic jednakowo dokładnych, obarczonych błędem systematycznym, należy stosować następujące wzory:











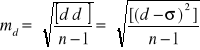
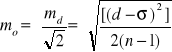
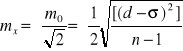
Dla różnic niejednakowo dokładnych, obarczonych błędem systematycznym, należy zastosować następujące wzory:










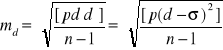
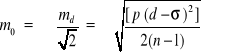
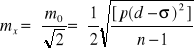
Przykład. Pomierzono kąty na pięciu stanowiskach dwukrotnie z jednakową dokładnością. Wyniki pomiarów zestawiono w tabeli:

Nr	Pomiar I	Pomiar II	d(s)	dd
1	1581010	1581045	-35	1225
2	1000518	1000528	-10	100
3	2001035	2001045	-10	100
4	1000555	1000520	+35	1225
5	301510	301500	+10	100
			-10	2750

Obliczyć średni błąd pojedynczego pomiaru oraz średni błąd podwójnego pomiaru kąta.

Obliczenie:







1

1

---