Energię aktywacji oblicza się z wzoru Arrheniusa wyznaczając stałą szybkości reakcji w różnych temperaturach: ![]()
Badanie aktywacji termicznej reakcji chemicznej.
Energia aktywacji (1)- najmniejsza energia jaką muszą mieć (w przeliczeniu na 1 mol) cząsteczki substratów , aby mogły wejść w daną reakcję.
Energię aktywacji oblicza się z wzoru Arrheniusa wyznaczając stałą szybkości reakcji w różnych temperaturach: ![]()
gdzie
k- stała szybkości reakcji
R - stała gazowa
T- temperatura
Ea- energia aktywacji
A- współczynnik częstości kolizji między cząsteczkami
Mechanizm reakcji (2)- - zbiór reakcji elementarnych składających się na daną przemianę chemiczną.
Koncepcja stanu przejściowego umożliwia precyzyjne wyjaśnienie cząsteczkowości reakcji oraz sensu fizycznego energii aktywacji.
Cząsteczkowość reakcji (2)- - w ujęciu stanu przejściowego, odpowiada liczbie cząsteczek, które w danym akcie elementarnym tworzą stan przejściowy.
Teoria stanu przejściowego (2)- opiera się na trzech podstawowych założeniach:
cząsteczki substratów przechodzą w produkty poprzez stan o maksymalnej energii, zwany stanem przejściowym
stan ten znajduje się w szybko ustalającej się równowadze z substratami
o szybkości reakcji decyduje szybkość rozpadu tego stanu na produkty
Energia aktywacji (Ea) jest więc różnicą energii stanu przejściowego![]()
i substratów![]()
.
Entalpia aktywacji![]()
- związana jest z energią tworzenia i rozrywania wiązań podczas reakcji:
Entropia aktywacji![]()
- charakteryzuje zmianę liczby stopni swobody cząsteczek substratów
w wyniku tworzenia stanu przejściowego.
Posiadając wyznaczone stałe szybkości reakcji w różnych temperaturach można wyznaczyć![]()
i![]()
w oparciu o rozwinięcie równania Eyringa
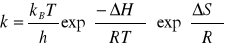
gdzie kB, h są odpowiednio stałymi: Boltzmanna, Plancka i gazową, T oznacza temperaturę , zaś![]()
i![]()
są funkcjami termodynamicznymi tworzenia kompleksu aktywnego (entalpia i entropia aktywacji)
Część doświadczalna
1. Aparatura i odczynniki:
termostat
IWE ELECTRONIC nr. fab. 120/2002
konduktometr
typ: OK.-102/1 firmy Redelkis klasa II
elektroda pomiarowa
Radelkis OK.-902
naczyńko pomiarowe
30% roztwór bromku t-butylu w CCl4
80% roztwór etanolu w wodzie
pipeta
stoper
2. Warunki pomiarów:
ciśnienie ogólne, zewnętrzne: 1004 hPa
temperatura zewnętrzna około: -100C
temperatura w laboratorium: 25 0C
3. Wykonanie ćwiczenia:
Pomiary kinetyki reakcji wykonano dla temperatur 28 0C i 36 0C.
Sposób wykonania ćwiczenia jest taki sam dla obydwu temperatur:
włączono termostat, nastawiając żądaną temperaturę
do naczynia pomiarowego wlano 80 ml 80% roztworu etanolu w wodzie.
naczynie pomiarowe umieszczono w termostacie, do naczynia włożono elektrodę
włączono konduktometr, odczekano ok. 20 min.
odczytano przewodnictwo elektrolityczne roztworu wodno-etylowego LWE
do naczynia pomiarowego z roztworem etanolu wlano 0,5 ml 30% roztworu bromku t-butylu jednocześnie mierząc czas i co minutę odczytując przewodnictwo elektrolityczne mieszaniny reakcyjnej LMR. Pomiary prowadzono do chwili zauważenia małych zmian przewodnictwa.
4. Wyniki pomiarów:
tabela nr 1. Przewodnictwo elektrolityczne badanego układu reakcyjnego.
Czas [min] |
|
|||||
|
T1=301 [K] |
T2=309 [K] |
||||
|
LWE = 2,1 [μS] |
LWE = 2,3[μS] |
||||
|
LMR [μS] |
L1 [μS] |
L2 [μS] |
LMR [μS] |
L1 [μS] |
L2 [μS] |
1 |
2,3 |
0,2 |
0,4 |
250 |
247,7 |
397,7 |
2 |
2,5 |
0,4 |
0,9 |
400 |
397,7 |
657,7 |
3 |
3,0 |
0,9 |
1,7 |
660 |
657,7 |
707,7 |
4 |
3,8 |
1,7 |
3,9 |
710 |
707,7 |
817,7 |
5 |
6,0 |
3,9 |
6,4 |
820 |
817,7 |
947,7 |
6 |
8,5 |
6,4 |
8,9 |
950 |
947,7 |
1047,7 |
7 |
11 |
8,9 |
11,9 |
1050 |
1047,7 |
1117,7 |
8 |
14 |
11,9 |
17,9 |
1120 |
1117,7 |
1147,7 |
9 |
20 |
17,9 |
32,9 |
1150 |
1147,7 |
1242,7 |
10 |
35 |
32,9 |
42,9 |
1245 |
1242,7 |
1372,7 |
11 |
45 |
42,9 |
47,9 |
1375 |
1372,7 |
1497,7 |
12 |
50 |
47,9 |
67,9 |
1500 |
1497,7 |
1597,7 |
13 |
70 |
67,9 |
82,9 |
1600 |
1597,7 |
1707,7 |
14 |
85 |
82,9 |
102,9 |
1710 |
1707,7 |
1747,7 |
15 |
105 |
102,9 |
112,9 |
1750 |
1747,7 |
1767,7 |
16 |
115 |
112,9 |
121,9 |
1770 |
1767,7 |
|
17 |
124 |
121,9 |
123,9 |
1780 |
1777,7 |
1787,7 |
18 |
126 |
123,9 |
126,9 |
1790 |
1787,7 |
1797,7 |
19 |
129 |
126,9 |
134,9 |
1800 |
1797,7 |
1807,7 |
20 |
137 |
134,9 |
143,9 |
1810 |
1807,7 |
1817,7 |
21 |
146 |
143,9 |
147,9 |
1820 |
1817,7 |
1817,7 |
22 |
150 |
147,9 |
152,9 |
1820 |
1817,7 |
---- |
23 |
155 |
152,9 |
162,9 |
---- |
---- |
---- |
24 |
165 |
162,9 |
172,9 |
---- |
---- |
---- |
25 |
175 |
172,9 |
177,9 |
---- |
---- |
---- |
26 |
180 |
177,9 |
182,9 |
---- |
---- |
---- |
27 |
185 |
182,9 |
185,9 |
---- |
---- |
---- |
28 |
188 |
185,9 |
188,9 |
---- |
---- |
---- |
29 |
191 |
188,9 |
192,9 |
---- |
---- |
---- |
30 |
195 |
192,9 |
197,9 |
---- |
---- |
---- |
31 |
200 |
197,9 |
205,9 |
---- |
---- |
---- |
32 |
208 |
205,9 |
207,9 |
---- |
---- |
---- |
33 |
210 |
207,9 |
209,9 |
---- |
---- |
---- |
34 |
212 |
209,9 |
211,9 |
---- |
---- |
---- |
35 |
214 |
211,9 |
214,9 |
---- |
---- |
---- |
36 |
217 |
214,9 |
215,9 |
---- |
---- |
---- |
37 |
218 |
215,9 |
216,9 |
---- |
---- |
---- |
38 |
219 |
216,9 |
---- |
---- |
---- |
---- |
III Opracowanie wyników
1. Sporządzono (korzystając z programu ORIGIN 5.0) wykresy zależności przewodnictw
elektrolitycznych L1=f(L2) roztworu bromku t-butylu dla temperatur (wykres nr 1
oraz nr 2).
2. Otrzymane w punkcie 1 wykresy aproksymowano do linii prostej i odczytano współczynnik
kierunkowy (wykres nr 3 i 4).
Równanie prostej (dla T1):
L1=1,07263L2 -5,11764 C1=1,07263
Równanie prostej (dla T2)
L2=1,19456L2 -178,18191 C2=1,19456
3. Obliczanie stałych szybkości reakcji:
Różnica czasów w których mierzone są zmiany stężenia jest stała, więc stałe szybkości reakcji
w badanych temperaturach obliczono wg równania:
![]()
gdzie ![]()
k- stała szybkości reakcji (dla reakcji pierwszego rzędu k [1/s])
c0- stężenie początkowe substratów [mol/dm3]
x - ubytki stężeń substratów [mol/dm3]
t2-t1 - kolejne odstępy czasowe [s]
- Stała szybkości reakcji dla T1=301 [K]
![]()
k1= ![]()
- Stała szybkości reakcji dla T2=309 [K]
![]()
k2=![]()
4. Obliczanie Entropii i entalpii aktywacji (![]()
,![]()
) na podstawie równania Eyringa:
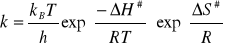
gdzie: ![]()
- stałą Boltzmanna
![]()
- stałą Plancka
R- stałą gazowa
T- temperatura
- Obliczanie ![]()
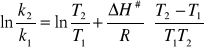
![]()
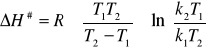
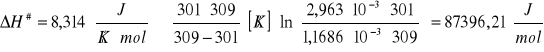
![]()
ΔH# = 87396,21![]()
Obliczanie ![]()
( dla T1 , k1)
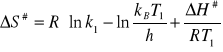
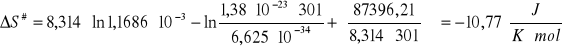
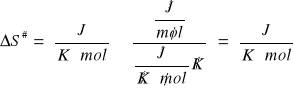
ΔS# = -10,77![]()
Graficzne wyznaczanie![]()
oraz ![]()
zależności lnk=f(1/T) (wykres nr 6).
Tabela nr 2
1/T |
Ln k |
3,322*10-3 |
-6,7519 |
3,236*10-3 |
-5,8216 |
Po przeprowadzeniu regresji liniowej zależności lnk=f(1/T) (wykres nr 5) otrzymano równanie linii prostej
Y=a+bX gdzie a=29,18364 b=-10817,4418
a) ![]()
wyliczamy ze współczynnika b:
![]()
![]()
![]()
![]()
![]()
b) ![]()
wyliczamy ze współczynnika a:
![]()
![]()
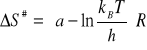
![]()
5. Obliczanie energii aktywacji (Ea ) i współczynnika częstotliwości zderzeń (A)
wg równania Arrheniusa:
![]()
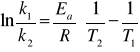
![]()
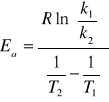
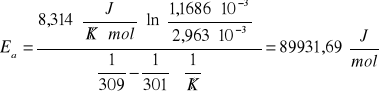
Ea = 89931,69 ![]()
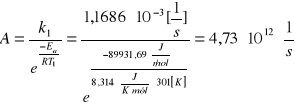
A= ![]()
Graficzne wyznaczanie Ea oraz A na podstawie wykresu zależności lnk=f(1/T) (wykres nr 5)
a) wyliczenie Ea
![]()
![]()
![]()
![]()
![]()
b) wyliczenie A
![]()
![]()
![]()
![]()
IV. Spostrzeżenia i wnioski:
1. Analiza wykresów zależności przewodnictw elektrolitycznych L1=f(L2) roztworu bromku t-butylu.
a) Analizując wykresy nr 1 i 2 stwierdza się, że wraz ze wzrostem temperatury wzrasta przewodnictwo
roztworu. Wzrost przewodnictwa wywołany jest wzrostem szybkości reakcji (wzrost stężenia produktu HBr i
jego dysocjacja), wraz ze wzrostem temperatury.
Dla niewielkich stężeń zmiana przewodnictwa L jest liniową funkcją zmian stężenia produktu, dlatego z
zależności L1=f(L2) dla stałych przedziałów czasowych, określa się współczynnik kierunkowy prostej co
pozwala z kolei wyznaczyć stałą szybkości reakcji.
Wyznaczone z współczynnika kierunkowego stałe szybkości reakcji wynoszą:
dla T1=301K k1= ![]()
dla T2=309K k2=![]()
Jak łatwo zauważyć wyznaczone k2 przyjmuje wartość większą niż k1. Stanowi to potwierdzenie, że szybkość reakcji wzrasta wraz ze wzrostem temperatury. Dla różnicy temperatur w których przeprowadzono doświadczenie (8K) szybkość reakcji wzrosła o 1,7944*10-3.
b) Analiza błędów.
Wg danych literaturowych(3) zmiana przewodnictwa L jest liniową funkcją zmian stężenia produktu.
Otrzymane wykresy zależności L1=f(L2) (wykres nr 1 i 2) znacznie różnią się od linii prostej co może być
wywołane:
nie dokładnością odczytu przewodnictwa ( wyskalowanie, skoki przewodnictwa poziom zanurzenia elektrody w badanym roztworze).
Aproksymowane do linii prostej wykresy L1=f(L2) ( nr 3 i 4) obarczone są dużym błędem wywołanym rozrzutem pomiarów , powodującym iż otrzymane stałe szybkości reakcji obarczone są błędem.
2. Analiza otrzymanych wartości: ![]()
, ![]()
, Ea , A
a) Analiza wartości ![]()
, Ea (wzajemne ich porównanie).
średnia wartość ![]()
średnia wartość Ea=89,93 [kJ/mol]
Analiza wartości entalpii i energii aktywacji potwierdza że wielkości te w niezbyt wysokich temperaturach
niewiele się od siebie różnią [1 ].
c) Analiza wartości ![]()
:
średnia wartość ![]()
Otrzymana wartość entropii aktywacji hydrolizy bromku t-butylu pozwala na oszacowanie liczby cząsteczek uczestniczących w stanie przejściowym, czyli może stanowić kryterium mechanizmu reakcji.
Na podstawie źródeł literaturowych [2] przyjmuje się, że jeżeli wartość ![]()
zmienia się w granicach od wartości dodatnich do -60 J/mol to reakcja jest jednocząsteczkowa, zaś od -60 do -110 J/mol dwucząsteczkowa. Analizowana reakcja jest więc reakcją jednocząsteczkową , czyli przebiega według mechanizmu SN1. Na ujemną wartość entropii aktywacji hydrolizy bromku t-butylu ma wpływ:
rozpuszczalnik ( jego polarność) powodująca solwatację stanu przejściowego zwiększającego orientacje cząsteczek, sprzyjająca porządkowaniu struktury stanu przejściowego i zmniejszeniu wartości entropii aktywacji.
polarność substratów i stanu przejściowego; im bardziej polarny jest stan przejściowy w stosunku do cząsteczek substratów tym wartość entropii jest mniejsza.
Brak danych literaturowych dla powyższych wielkości powoduje, że analiza wyników doświadczenia jest nie pełna
d) Analiza badanej reakcji.
Analiza wartości ![]()
wykazała , że badana reakcja przebiega według mechanizmu SN1
Reakcja pomiędzy bromkiem tert-butylu i jonami wodorotlenkowymi, powodująca utworzenie alkoholu tert-butylowego, przebiega więc według kinetyki pierwszego rzędu, czyli jej szybkość zależy od stężenia tylko jednego substratu - bromku tert-butylu.
t-(CH3)3-C-Br + OH-![]()
t-(CH3)3-C-OH + Br - ![]()
Cząsteczka bromku tert-butylu dysocjuje powoli na jon bromkowy i kation tert-butylowy
(1) t-(CH3)3-C-Br ![]()
t-(CH3)3-C+ + Br-- Powoli
Następnie karbokation łączy się szybko z jonem wodorotlenkowym, w wyniku czego tworzy się cząsteczka alkoholu tert-butylowego.
t-(CH3)3-C+ + OH- ![]()
t-(CH3)3-C-OH + Br - Szybko
Etapem określającym szybkość reakcji jest etap powolnego rozrywania wiązania C-Br.
Energia potrzebna do rozerwania wiązania C-Br uzyskiwana jest w wyniku tworzenia się licznych wiązań
jon-dipol między jonami dwóch rodzajów a cząsteczkami rozpuszczalnika.
![]()
W celu potwierdzenia poprawności mechanizmu badanej reakcji odwołano się do źródła
literaturowego [„Chemia organiczna ” R.T. Morrison, R.N. Boyd tom 1 str 536-555 . PWN Warszawa 1998]
Literatura:
[1] P.W Atkins: Chemia fizyczna PWN 1998
[2] J. Lubczak, E. Chmiel Teoria stanu przejściowego, Chemia w szkole 1988
[3] Literaturowy przebieg ćwiczenia
[4] Chemia organiczna R.T. Morrison, R.N. Boyd PWN Warszawa 1998
substrat
Stan przejściowy
bardziej polarny niż substrat, bardziej stabilizowany przez solwatację
produkty
Gdzie:
LWE- przewodność roztworu
wodno-etanolowego
LMR -przewodność mieszaniny
Reakcyjnej
L- przewodność Br-
L= LMR- LWE
VERTE