1ET-DI Rzeszów, 15.01.2011

Andrzej Deryło

Sprawozdanie z ćwiczenia nr 48

Temat: Wyznaczanie ogniskowej soczewki metoda Bessela.

I. Zagadnenia do samodzielnego opracowania:

Soczewka: Soczewką nazywamy ciało przezroczyste ograniczone dwiema powierzchniami

kulistymi (wypukłymi lub wklęsłymi) lub jedną powierzchnią kulistą, a jedną płaską.

Każda powierzchnia kulista soczewki ma swój środek krzywizny i odpowiadający jej

promień (np. r1 i r2). Prostą przechodzącą przez oba środki nazywa się osią główną

soczewki. Promienie biegnące równolegle do osi głównej skupiają się po załamaniu w

soczewce w punkcie zwanym ogniskiem soczewki (F1 i F2). Każda soczewka ma dwa

ogniska leżące po przeciwnych stronach soczewki. Odległość tego punktu do środka

soczewki nosi nazwę ogniskowej soczewki (f1 lub f2). Ogniskowe soczewek bardzo

cienkich są sobie równe. Przy pomocy soczewek uzyskuje się odwzorowania

przedmiotów. W celu wykreślenia obrazu przedmiotu otrzymywanego przy użyciu

cienkiej soczewki, rysujemy dwa promienie:

a) promień przechodzący przez środek geometryczny soczewki, który nie ulega

załamaniu,

b) promień równoległy do głównej osi soczewki, który po załamaniu w soczewce

przechodzi przez ognisko.

Poniższy rysunek przedstawia konstrukcję powstającego obrazu O dla

przedmiotu P.

Korzystając z podobieństwa trójkątów ABF i DCF można wyprowadzić równanie

soczewki:

Powstawianie obrazu w soczewkach:
Położenie przedmiotu: f<x<2f

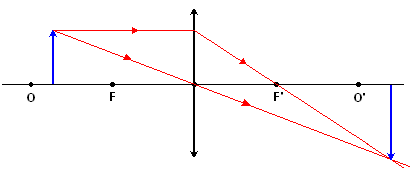
Cechy obrazu:
- rzeczywisty; utworzony przez przecięcie promieni świetlnych
- odwrócony
- powiększony; p>1
Odległość obrazu:
- y>2f

Położenie przedmiotu: x=2f

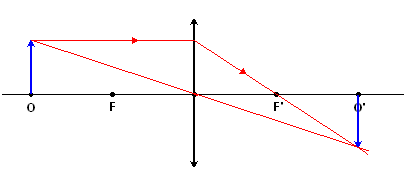
Cechy obrazu:
- rzeczywisty; utworzony przez przecięcie promieni świetlnych
- odwrócony
- niepowiększony rzeczywistych rozmiarów; p=1
Odległość obrazu:

- y=2f

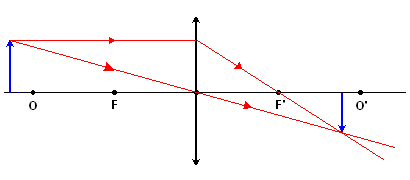
Położenie przedmiotu: x>2f

Cechy obrazu:
- rzeczywisty; utworzony przez przecięcie promieni świetlnych
- odwrócony
- pomniejszony; p<1
Odległość obrazu:
- f<y<2

Definicja powiększenia obrazu: Powiększenie układu optycznego jest stosunkiem rozmiaru obrazu do rozmiaru przedmiotu. Powiększenie jest wielkością bezwymiarową i może przyjmować wartości większe od 0. Powiększenie p > 1 oznacza rzeczywiste powiększenie obrazu podczas gdy p < 1 - jego pomniejszenie. Niektórzy autorzy przypisują powiększeniu wartość ujemną, gdy obraz jest odwrócony. Z punktu widzenia optyki geometrycznej powiększenie zależy tylko od geometrii układu optycznego i może być dowolnie duże. Jednak z powodu falowej natury światła, przy pewnym powiększeniu pogarsza się jakość obrazu. Jest to spowodowane skończoną zdolnością rozdzielczą przyrządów optycznych. W zależności od rodzaju obrazu i przeznaczenia układu optycznego, definiuje się powiększenie liniowe (zwane po prostu powiększeniem) lub powiększenie kątowe.

II. Wykonanie ćwiczenia

1. Ustawić układ pomiarowy jak na powyższym rysunku, odczytać ze skali

odległość e między przedmiotem P a ekranem E.

2. Przesuwając soczewkę w kierunku ekranu znaleźć takie jej położenie y1, aby na

ekranie widoczny był powiększony ostry obraz przedmiotu. Zmierzyć również

wysokość powstałego obrazu H1.

3. Przesuwając dalej soczewkę w kierunku ekranu przy niezmienionym e znaleźć

drugie jej położenie y2 takie, aby na ekranie powstał ostry pomniejszony obraz

przedmiotu. Zmierzyć wysokość powstałego obrazu H2 .

4. Czynności wymienione w punkcie 2 i 3 powtórzyć 10 razy.

5. Korzystając z odpowiedniej zależności obliczyć ogniskową soczewki f i wysokość przedmiotu

H, pamiętając o zależności
. Wyliczyć średnią wartość

e [mm]	y1+/- u(y1) [mm]		y2 +/- u(y2) [mm]		a +/- u(a) [mm]		H1 +/- u(H1) [mm]		H2 +/- u(H2) [mm]
805	465	+/- 2,0248	340	+/- 2,5298	125	+/- 3,2404	9	+/- 0,4595	5	+/- 0,3162
805	472	+/- 2,0248	338	+/- 2,5298	134	+/- 3,2404	8,5	+/- 0,4595	5	+/- 0,3162
805	469	+/- 2,0248	336	+/- 2,5298	133	+/- 3,2404	9	+/- 0,4595	5	+/- 0,3162
805	468	+/- 2,0248	341	+/- 2,5298	127	+/- 3,2404	9	+/- 0,4595	4	+/- 0,3162
805	470	+/- 2,0248	337	+/- 2,5298	133	+/- 3,2404	8	+/- 0,4595	5	+/- 0,3162
805	471	+/- 2,0248	335	+/- 2,5298	136	+/- 3,2404	8	+/- 0,4595	5	+/- 0,3162
805	470	+/- 2,0248	338	+/- 2,5298	132	+/- 3,2404	8	+/- 0,4595	5	+/- 0,3162
805	469	+/- 2,0248	333	+/- 2,5298	136	+/- 3,2404	8	+/- 0,4595	5	+/- 0,3162
805	467	+/- 2,0248	334	+/- 2,5298	133	+/- 3,2404	8,5	+/- 0,4595	5	+/- 0,3162
805	470	+/- 2,0248	336	+/- 2,5298	134	+/- 3,2404	8	+/- 0,4595	5	+/- 0,3162

f +/- u(f) [mm]		p +/- u(p) [-]		D +/- u(D)[D]		h +/- u(h) [mm]
196,3975	+/- 0,2740	1,3416	+/- 0,1572	0,0051	+/- 6,888	6,7082	+/- 0,4435
195,6736	+/- 0,2724	1,3038	+/- 0,2727	0,0051	+/- 7,044	6,5192	+/- 1,0110
195,7565	+/- 0,2721	1,3416	+/- 0,2739	0,0051	+/- 6,985	6,7082	+/- 1,0272
196,2410	+/- 0,2702	1,5000	+/- 0,3228	0,0051	+/- 6,637	6,0000	+/- 0,9851
195,7565	+/- 0,2721	1,2649	+/- 0,2717	0,0051	+/- 6,985	6,3246	+/- 0,9950
195,5059	+/- 0,2731	1,2649	+/- 0,2717	0,0051	+/- 7,161	6,3246	+/- 0,9950
195,8388	+/- 0,2718	1,2649	+/- 0,2717	0,0051	+/- 6,927	6,3246	+/- 0,9950
195,5059	+/- 0,2731	1,2649	+/- 0,2717	0,0051	+/- 7,161	6,3246	+/- 0,9950
195,7565	+/- 0,2721	1,3038	+/- 0,2727	0,0051	+/- 6,985	6,5192	+/- 1,0110
195,6736	+/- 0,2724	1,2649	+/- 0,2717	0,0051	+/- 7,044	6,3246	+/- 0,9950
195,8106	+/- 0,2723	1,3116	+/- 0,2658	0,0051	+/- 6,982	6,4078	+/- 0,9453

Wartości pogrubione to wartości średnie poszczególnych wielkości oraz ich błędów.

III. Obliczenia:

Błędy: u(y1), u(y2), u(H1), u(H2) zostały obliczone w programie Excel za pomocą polecenia odchylenie

standardowe średniej.

Błąd pomiarowy u(e) obliczamy metodą typu B:

Pozostałe wartości błędów obliczamy za pomocą niepewności standardowej złożonej:

IV. Wnioski:

Celem ćwiczenia było wyznaczanie ogniskowej soczewki metodą Bessela. Otrzymany wynik (195,81 +/- 0,27) mm jest obarczony niewielkim błędem, więc można stwierdzić, że ćwiczenie zostało wykonane we właściwy sposób.

---