MECHANIKA Mechanika jest jednym z działów fizyki: stanowi
podstawę do zrozumienia nie tylko innych działów tej nauki, ale
także innych nauk przyrodniczych. Zajmuje się ruchem obiektów
materialnych. Dzieli się na dwa podstawowe działy:- kinematykę
- dynamikę(kinetyke,statykę) Kinematyka punktu materialne
Kinematyka zajmuje się opisem ruchu ciał, bez wnikania w prz
yczyny ich występowania. Wprowadza podstawowe pojęcia wi
elkości fizycznych, związanych z ruchem i bada, jakie związki
i zależności występują pomiędzy tymi wielkościami.Najprostszy
opis ruchu otrzymuje się rozważając tzw.punkt materialny,prze
z który rozumie się wyidealizowany obiekt, o dowolnej masie m
, którego rozmiary liniowe r są nieskończenie małe (r → 0).W ki
nematyce punktu materialnego wyróżnia się niektóre rodzaje r
uchów prostych, dzieli się je także ze względu na ich wymiar
owość na ruchy 1-, 2- i 3-wymiarowe, inaczej na liniowe, płaski
e i przestrzenne.Cechą charakterystyczną ruchów jest ich kier
unkowość, dlatego opisując ruch korzysta się z pojęcia i właściw
ości wektorów.Podstawowe definicje kinematyczneprzemieszczen
ie![]()
-jeżeli punkt materialny w chwili t1 znajdował się w punkc
ie A, a w chwili t2 w punkcie B, to niezależnie od tego jak on się
poruszał między tymi punktami, przez przemieszczenie rozumiemy w
ektor ![]()
, o początku wektora w punkcie A i jego końcu w punkcie B.
droga(S)-jest to odległość (wielkość skalarna) jaką przebywa ciało
po trajektorii ruchu. prędkość chwilowa - określa szybkość przemi
eszczania się ciała w danej chwili; jest ona określona wzorem: 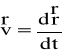
prędkość średnia - jeżeli ciało przebywa drogę ![]()
w czasie ![]()
, to
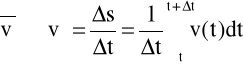
przyspieszenie - określa szybkość zmiany
prędkości w czasie![]()
Wielkości zdefiniowane powyżej stosuje się
zasadniczo do opisu ruchu postępowego, in. zwanego translacyjnym.
Aby opisywać drugi rodzaj ruchu, tj. ruch obrotowy, stosuje się analogi
czne do powyższych wielkości takie jak:przemieszczenie kątowe, pręd
kość kątową i przyspieszenie kątowe.Kinematyka ruchu obrotowego
Istotną cechą ruchu obrotowego punktu materialnego jest istnienie tak
iego punktu (lub osi), względem którego odległość położenia punktu
nie ulega zmianie. Odległość tę nazywamy promieniem obrotu, przemies
zczenie punktu charakteryzuje się za pomocą kąta, który zostaje zakre
ślony przez poruszający się punkt. Kąt, z natury rzeczy, jest wielkością
skalarną, jednak bardzo małym kątom elementarnym ![]()
przypisuje
się właściwości wektorowe.Na podstawie umowy - elementarne prze-mi
eszczenie kątowe ![]()
, co do modułu jest równe wartości kąta ![]()
, zaś
kierunek (zwrot) tego wektora określony jest tzw. regułą śruby prawo skręt
nej - jest prostopadły do płaszczyzny, wyznaczonej przez kąt ![]()
i rów
nocześnie równoległy do osi obrotu. W ruchu obrotowym, operuje się pojęc
iami -prędkość kątowa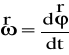
oraz przyspieszenie kątowe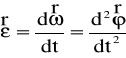
Łatwo zauważyć, że kierunek prędkości kątowej ![]()
jest taki sam jak wekt
ora ![]()
i leży na osi obrotu ciała.Przyspieszenie styczne - przyspieszenie
ątowePunkt materialny poruszając się po okręgu o promieniu R może wyk
onywać ruch obrotowy w taki sposób, że wartość prędkości v (zawsze stycz
na do toru ! ) zmienia się w czasie - oznacza to, że występuje przyspiesze
nie ruchu Punktu, które nosi nazwę przyspieszenia stycznego i zwykle oznac
zane jest jako ![]()
.Tak więc w ruchu po okręgu, całkowite przys
ieszenie![]()
Środek masy- Jednym z pojęć, przydatnych do opisu
ruchu ciał, jest środek masy. Jest to szczególny punkt, z definicji - taki, wzg
lędem którego suma Momentów masy układu (zbioru punktów materialnyc
lub ciała sztywnego) jest równa zero. Moment masy punktu A o masie m
względem punktu 0 jest równy![]()
Moment masy układu (i = 1, 2, ..
., n) punktów materialnych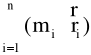
Wektor ![]()
, określający położenie
rodka masy S, jest zdefiniowany za pomoą
wzoru 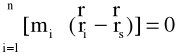
Stąd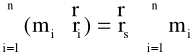
oraz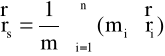
gdzie: 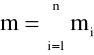
- jest całkowitą masą układu. Dla układu o ciągłym rozkuł
adzie masy (ciało sztywne) położenie środka masy jest opisane wzorem
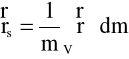
DYNAMIKA PUNKTU MATERIALNEGODynamika za
jmuje się przyczynami ruchu i jego zmia-nami , spowodowanymi wzajemnym
oddziaływaniem ciał na siebie.Podstawą tzw. mechaniki klasycznej są trzy prawa z
w. zasadami dynamiki Newtona, które zostały opubli-kowane w r. 1687.
Treść tych zasad odnosi się do punktów materialnych.Zasady dynamiki Newtona
I zasada dynamiki Newtona:Jeśli na ciało nie działają żadne siły, lub ich suma
(wektorowa) jest równa zeru, to ciało pozostaje w spoczynku lub porusza się ruche
m jednostajnym prostoliniowym.Zasada ta, zresztą tak jak pozostałe dwie, jest sp
ełniona tylko w tzw. układach inercjalnych, tj. układach odniesienia poruszający
ch się ze stałą prędkością.Dotychczasowe doświadczenia wskazują, że każdy ukł
ad odniesienia związany z gwiazdami stałymi jest układem inercjalnym. Także prak
tycznie rzecz biorąc, układy związane z Ziemią można w większości przypadków u
ważać za układy inercjalne.Należy zauważyć, że każdy układ odniesienia poruszający
się ze stałą prędkością względem układu inercjalnego jest także układem inercja
nym.II zasada dynamiki Newtona:Przyspieszenie wywołane przez jedną lub więc
ej sił działających na ciało jest proporcjonalne do wypadkowej tych sił, zgodne z jej
kierunkiem i odwrotnie proporcjonalne do masy ciała.![]()
lub, uwzględniając
definicję pędu ![]()
, ![]()
Występująca we wzorze masa m, jest wielkością charakterystyczną dla danego CIA
ła i stanowi miarę jego bezwładności - można ją określić porównując z wzorcem masy.
II zasada dynamiki Newtona wprowadza pojęcie siły i równocześnie stanowi jej definicję.
III zasada dynamiki Newtona:Wzajemne oddziaływanie dwóch ciał jest zawsze rów
ne i przeciwnie skierowane![]()
Można zauważyć, że I zasada dynamiki Newtona stanowi jakby szczególny przypadek
II zasady. Została ona jednak wyróżniona jako osobne prawo z powodu głębszych treś
dnych przestrzennych i czasu z jednego układu odniesienia do innego poruszającego się
Ruchem jednostajnym prostoliniowym względem pierwszego. W transformacji tej czas i o
dległości pomiędzy dwoma dowolnymi punktami pozostają stałe, czyli są niezależne od uk
ładu odniesienia. Transformacja Galileusza jest zgodna z klasycznymi wyobrażeniami
wszystkich układach inercjalnych, tj. obserwatorzy z różnych układów inercjalnych stw
erdzą taki sam ruch badanego obiektu. Ruch jednostajny prostoliniowy jest nierozró
żnialny od spoczynku - obserwując zjawiska mechaniczne nie jesteśmy w stanie go rozró
nić.Układy nieinercjalne - siły bezwładności: Zasady dynamiki Newtona - odnoszą Si
ę tylko do układów inercjalnych. Układ odniesienia jest nieinercjalny, jeśli:
- w ruchu postępowym porusza się z pewnym przyspieszeniem względem układu inercja
lnego, -wykonuje ruch obrotowy względem układu inercjalnego. zasady zachowania:
pędu i momentu pęduII zasadę dynamiki Newtona można zapisać w postaci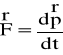
która jest obowiązująca zarówno w przypadku pojedynczej cząstki, jak i układu sztywno zwi
ązanych ze sobą cząstek lub bryły sztywnej. Można łatwo także pokazać, że jest ono słuszne
w odniesieniu do zbioru oddziaływujących ze sobą ciał, które nie są ze sobą sztywno związane.
Pęd:Jest to wielkość fizyczna wyrażająca się wzorem:
Zasada zachowania pędu:
Jeżeli na ciało lub układ ciał nie działa żadna siła zewnętrzna (pochodząca od innego ciała), to
całkowity pęd układy jest stały.
Zasada zachowania momentu pędu mówi: że dl
jest stała. Jedną z bardziej widowiskowych konsekwencji istnienia tej zasady są znaczne
puje jego ruch i ciało się ulega przemieszczeniu. W mechanice wprowadza się pojęcie pracy. P
odstawowa jej definicja jest związana z pojęciem pracy elementarnej, opisanej wzorem
![]()
gdzie ![]()
jest elementarnym przemieszczeniem ciała, zachodz
ącym w czasie dt . Praca jest wielkością skalarną.Pracę wykonaną przez siłę ![]()
przy prz
emieszczeniu cząstki z punktu 1 do punktu 2 obliczamy ze wzoru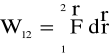
W mecha
nice wielkość opisaną wzorem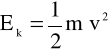
nazywa się energią kinetyczną ciała.siły zachow
awcze - energia potencjalna Jeżeli ciało, w każdym punkcie rozważanej przestrzeni, jest podd
ane działaniu ze strony innych ciał - mówimy - że cząstka znajduje się w polu sił.Pole, które ni
e zmienia się w czasie nazywamy polem stacjonarnym.Pole stacjonarne, w którym praca wyk
onana nad ciałem zależy tylko od początkowego i końcowego położenia ciała (tzn. nie zależy o
d drogi po którym ciało się poruszało), nazywamy polem zachowawczym a siły tego pola zwie
się siłami zachowawczymi.Przykładem siły niezachowawczej może być siła tarcia, która z Nat
ury swojej ma zawsze przeciwnie skierowany zwrot do wektora prędkości, a zatem i do element
arnych przemieszczeń ![]()
.zasada zachowania energii mechanicznejDla sił zachowawczych
pracę możemy więc przedstawić ![]()
zaś wcześniej zostało pokazane, że prac
a wykonana nad cząstką (dla sił zachowawczych i niezachowawczych) powoduje zmianę jej en
ergii kinetycznej![]()
Porównując ze sobą te dwa wyrażenia otrzymujemy
![]()
=> ![]()
Wynika stąd, że suma energii poten
cjalnej i energii kinetycznej ciała w polu sił zachowawczych jest taka sama w każdym dowol
ym punkcie tego pola.Wielkość tę, zapisując ogólnie E = Ep + Ek mnazywamy całkowitą en
ergią mechanicznąZasadaZachowaniaEnergiiMechanicznej: W układzie izolowanym ciał
całkowita energia mechaniczna nie ulega zmianie Ec = Ek + Ep = constans związek energii
potencjalnej z siłami pola:Znając postać energii potencjalnej, tj. funkcję Ep = Ep(x,y,z) moż
na określić siłę działającą na ciało w każdym punkcie pola.Siła zachowawcza jest równa u
jemnemu gradientowi energii potencjalnej. energia kinetyczna ruchu obrotowego bryły szty
wnejDla elementarnej masy dm bryły sztywnej obracającej się wokół osi
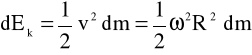
gdzie R jest odległością elementu o masie dm od osi o
brotu.Dla bryły sztywnej - energia kinetyczna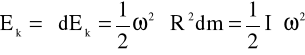
praca momentu sił zewnętrznych Jeśli na bryłę działają siły zewnętrzne, to ich praca dW
powoduje zmianę energii kinetycznej dEk , zatem
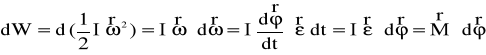
Praca w ruchu Obr
otowym, wykonana przez moment sił zewnętrznych, w skończonym przedziale kątowym, w
yraża się więc wzorem![]()
który jest analogiczny do zapisu pracy w ruchu postęp
owym.CIEPŁO Termodynamika stosuje metodę opisu fenomenologiczną, opartą bezpośr
ednio na danych doświadczalnych i bada jedynie makroskopowe zjawiska, nie interesując s
ię ich obrazem mikroskopowym. Podstawą termodynamiki są zasady termodynamiki.Fizyka
cząsteczkowa bada budowę i własności materii; posługuje się pojęciami teorii kinetyczno - mole
kularnej i stosuje opis statystyczny ruchu zbioru dużej liczby drobin. Termodynamika i fizyka stat
ystyczna uzupełniają się wzajemnie, wiążą ze sobą wielkości (obrazy) - makroskopowe i mikr
oskopowe procesów cieplnych. Dynamika procesów cieplnych jest bardzo skomplikowan
a, stąd też wszystkie ilościowe rozważania termodynamiki dotyczą stanów równowagi układ
ów i procesów odwracalnych.Przez stan równowagi termodynamicznej (cieplnej) rozumiemy
taki stan, w którym układ może pozostawać dowolnie długo a wszystkie parametry stanu (np. c
iśnienie, objętość, temperatura, ......) mają określone wartości i nie ulegają zmianie.Przez pro
ces odwracalny, in. nazywany przemianą równowagową lub kwazistatyczną rozumie się tak
i proces, który składa się z ciągłego zbioru kolejnych stanów równowagi. Realne przemian
y mogą być uważane za odwracalne, jeśli zachodzą dostatecznie powoli.Jednym z podst
awowych pojęć termodynamicznych jest wielkość zw. energią wewnętrzną ciała, zwykle ozn
aczana U . Jest to całkowita energia, jaką posiada ciało (kinetyczna i potencjalna oddziały
wań wewnętrznych) z wyłączeniem energii kinetycznej i potencjalnej ciała wynikających z
oddziaływań zewnętrznych pól.Energia wewnętrzna - mówimy - jest funkcją stanu układu,
tzn. ma zawsze tę samą wartość w danym stanie, niezależnie od „historii” układu.Temperatura
jest jednym z tzw. parametrów stanu i jest także funkcją stanu. Dwa ciała mają tę SA
mą temperaturę, jeśli między nimi nie ma przekazywania ciepła.Do określenia temperatury stosuj
e się powszechnie termometry, które są w sposób umowny skalowane. Używane są róż
e skale termometryczne. Najbardziej rozpowszechnione jest stosowanie skali Celsjusza, która
polega na przyjęciu, że: -w warunkach ciśnienia 1 atm - temperatura topnienia lodu wynosi 0
0C, a wrzenia wody 100 0C, -wybrana tzw. cecha termometryczna (np. rozszerzalność objętościo
wa rtęci) zależy liniowo od temperatury.II zasada termodynamiki pozwoliła dopiero zbudowa
ć skalę , która nie posiada wspomnianej wady. Nosi ona nazwę bezwzględnej termodynamic
znej skali temperatur .Jednostką temperatury bezwzględnej jest 1 K (kelwin) = 1 0C. Pom
iędzy skalą Kelwina i skalą Celsjusza zachodzi związek T = t +273,15 gdzie: T - tempera
ura w skali bezwzględnej; t - w skali Celsjusza.Równanie stanu gazu doskonałego Najprostsz
ą do opisu termodynamicznego formą materii jest jej stan gazowy. Badania przeprowadzon
dla różnych gazów pokazują jednak, że ich zachowanie w zależności od temperatury i ciś
nienia są nieco różne, przy czym praktycznie brak różnic występuje dla gazów dostateczni
e rozrzedzonych. Dlatego w termo dynamice wprowadzono pojęcie tzw. gazu doskonałego o
cechach charakterystycznych dla gazów Rozzedzonych o niewielkich gęstościach. Doświadcz
enia pokazują, że dla ustalonej ilości (tej samej liczby drobin) takich gazów jest spełnione równ
anie 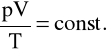
gdzie: p - ciśnienie gazu, V - jego objętość, T - jego temperatura. W szczegół
lności (prawo Avogadro) 1 mol każdego gazu zawiera zawsze tę samą liczbę drobin NA =6,022
x 1023 i zajmuje te samą objętość Vm zw. objętością molową. Stąd wynika, że dla 1 mola, stała
występująca w podanym wzorze posiada określoną wartość; sałą tę przyjęto oznaczać symbolem
R i z danych doświadczalnych wynika jej wartość R = 8,31 J/(mol K) Tak więc równanie wyż
ej podane, dla 1 mola może być przepisane w postaci pVm = RTa dla 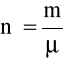
moli ( m - ma
sa rozpatrywanego gazu; ![]()
- jest masą 1 mola gazu, czyli masą cząsteczkową wyrażoną
w jednostkach masy)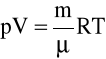
Równanie Clapeyrona czyli równanie stanugazu dosko
ałego wyraża ścisłą zależność pomiędzy bardzo istotnymi parametrami określającymi
stan gazu: liczbą jego moli, jego ciśnieniem, objętością i temperaturą. Ma ono prostą postać:
PV = nRT Ciepło dostarczone do układu, lub przekazane od układu wiąże się ze zmianami tem
peratury. Ilość ciepła potrzebna do zmiany temperatury ciała o wartość jednostkową jest wielko
ścią charakterystyczną dla danego ciała i nosi nazwę pojemności cieplnej tego ciała. Z tego okre
ślenia wynika wzór delfinicyjny pojemności cieplnej ciała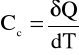
wyrażanej w jednostce J/K
. Uwzględniając definicję ciepła właściwego substancji c - ilość ciepła potrzebna do zmiany
o jednostkę temperatury jednostki masy danej substancji - jeśli masa substancji wynosi m , to
zachodzi oczywista relacja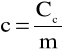
przy czym ciepło właściwe wyrażamy w jednostkach J/(kg
K). W termodynamice najczęściej stosowaną jednostką ilości materii jest 1 mol; w związk
u z tym definiuje się pojęcie ciepła molowego C jako ilości ciepła, potrzebną do zmiany tem
eratury o jednostkę dla 1 mola substancji. Ponieważ masa 1 mola jest równa masie
cząsteczkowej/atomowej ![]()
wyrażonej w jednostkach masy, wynika stąd prosty związek
![]()
Ciepło molowe jest wyrażane w jednostkach J/(mol K).Ilość ciepła dostarcz
oną do układu n' moli substancji obliczamy więc, stosując wzór 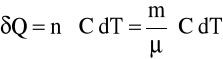
gdzie m - jest masą danej substancji.ZASADY TERMODYNAMIKI Zerowa zasada te
rmodynamikiWyznaczenie wartości wielkości fizycznych często odbywa się drogą pośr
ednią, ponadto wymaga użycia odpowiednich przyrządów pomiarowych i odniesienia ich
do wzorców. W ramach termodynamiki istnieje konieczność uściślenia postępowania w tej
sprawie - rolę tę spełnia tzw. „zerowa” zasada termodynamiki, którą można sformułować:
Jeśli układy A i B mają tę samą wartość dowolnej funkcji stanu i podobnie zachodzi dla
układów B i C, to układy A i C również mają tę samą wartość tej funkcji stanu.
I zasada termodynamikiEnergia wewnętrzna - ogólnie - ulega zmianie, jeśli co najmniej je
den z parametrów (p, V, T, ..), określających stan układu, zmienia swą wartość.Zmiana tych
parametrów, a co za tym idzie zmiana energii wewnętrznej ![]()
może nastąpić w w
yniku zajścia dwóch procesów: -wykonania pracy nad układem W -dostarczenia ciepła
do układu Q.Termin ciepło zwykle kojarzony jest z pewną formą energii; jednak w fizyc
e nazwę tę odnosi się do procesów, w których energia zostaje przeniesiona dzięki istnieniu r
żnicy temperatur między oddziałującymi ze sobą ciałami.Praca i ciepło należą do tzw.
przepływów (energii) - w opisie drobinowym różnią się one tym, że:- praca jest przepływ
em uporządkowanego ruchu cząsteczek - ciepło jest przepływem energii ruchu chaotyczn
ego drobinI zasada termodynamiki orzeka więc:Zmiana energii wewnętrznej układu jest rów
na sumie, pracy wykonanej nad układem i ciepła
dostarczonego do układu. co można zapisać wzorem![]()
Jednak bardziej popraw
nym zapisem treści I zasady termodynamiki jest postać różniczkowa:![]()
gdzie:
dU matematycznie oznacza różniczkę zupełną, czyli zachodzi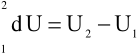
zaś![]()
stanowią infinitezymalne ilości pracy i ciepła, ale nie są różniczkami zupełnymi i ich wartości
zależą od sposobu realizacji przemiany. Przemiany stanu gazu doskonałego:Procesy, w wy
iku których następuje zmiana stanu termodynamicznego materii nazywamy przemianami. P
rzemiany mogą być w różny sposób realizowane, o czym wspominano już wcześniej. Szczeg
ólne jednak znaczenie mają przemiany:- izochoryczna, zachodząca przy warunku zachowa
nia stałej objętości, tzn. gdy zachodzi V = const.- izobaryczna, dla warunku stałego ciś
nienia, tj. p = const. - izotermiczna, gdy temperatura nie ulega zmianie, T = const.- adiab
atyczna, która zachodzi w warunkach braku wymiany ciepła z otoczeniem, tzn. gdy
![]()
.Trzy pierwsze przemiany - izochoryczna, izobaryczna i izotermiczna - są o
pisywane bezpośrednio przez równanie stanu gazu doskonałego, przy postawieniu opow.
iednich, wyżej wymienionych warunków stałości.Np. dla T = const., otrzymuje się równa
nie p V = const., znane jako prawo Boyle'a-Mariotte'a.II zasada termodynamiki
Dotyczy ona procesów termodynamicznych cyklicznych - w jej ramach rozważa się pro
cesy:= odwracalne gdy przechodzenie ze stanu 1 do stanu 2 zachodzi w waru
nkach stałej równowagi termodynamicznej= nieodwracalne gdy prz
ejścia zachodzą w warunkach braku równowagi termodynamicznej (cieplnej,
mechanicznej, elektrycznej, ......); gdy występują niejednorodności w różnych części
ach układu.S. Carnot (1796 - 1832) - przeprowadził rozważania nt. działania silników
cieplnych, w których mogą zachodzić oba wyżej wspomniane procesy, a ciałem robo
czym jest gaz doskonały.Wykazał on teoretycznie, że najbardziej sprawny taki silnik cyk
iczny otrzymuje się wtedy, gdy jego działanie oparte jest na dwu procesach izotermic
znych (w temperaturach T1 i T2) i dwóch przemianach adiabatycznych - przy czym są o
ne procesami odwracalnymi. Zestaw takich przemian nosi nazwę cyklu Carnota.Ogólnie,
sprawność energetyczna silnika cieplnego jest definiowana![]()
gdzie: ![]()
- jest pra
cą wykonaną przez układ (gaz doskonały); Q1 - ciepłem dostarczonym do układu.
Łatwo można wykazać, że dla cyklu Carnota zachodzi relacja![]()
w której ![]()
ma znaczenie ujemnego ciepła dostarczonego do układu z chło
dnicy. Relacja ta jest ogólnie ważna zarówno dla występowania w cyklu procesów od
wracalnych jak i nieodwracalnych. Jeśli cykl Carnota składa się z procesów wyłącznie
odwracalnych, z powyższego wzoru otrzymuje się![]()
Jeśli w cy
klu Carnota występuje chociaż jedna przemiana nieodwracalna, sprawność jego
![]()
Z rozważań Carnota wynika wniosek: sprawność silnika cieplnego jest
zawsze mniejsza od 1, tzn. zawsze część ciepła pobranego ze źródła musi być przekaza
na do chłodnicy - jeśli silnik cieplny ma pracować w sposób ciągły - cykliczny.Ist
nieje kilka klasycznych sformułowań II zasady termodynamiki; jednym z nich jest
Kelvina - Plancka, które stwierdzanie można zbudować silnika pracującego cyklicznie,
którego jedynym rezultatem by było pobieranie ciepła ze źródła i wykonyw
anie równoważnej mu ilości pracy.III zasada termodynamikiJeżeli rozważyć odwrotn
y cykl Carnota, to łatwo zauważyć, że wszelkie wielkości takie jak praca i ciepło zmie
niają swoje wartości na przeciwne w stosunku do normalnego cyklu Carnota, a więc m.in.
. - praca wykonana nad ciałem roboczym W > 0 , - ciepło Q2 > 0 , tzn. jest ono po
bierane z chłodnicy. Przy skończonej pojemności cieplnej chłodnicy, temperatura chłodni
cy zatem maleje. Odwrotny cykl Carnota można zastosować więc do obniżania tempera
tury chłodnicy T2 aż do zera bezwzględnego. W każdym cyklu - jednak tylko część
(nigdy całość) energii wewnętrznej chłodnicy może zostać przeniesiona w postaci ciepł
a Q2 Stąd III zasada termodynamiki, zwana także postulatem Nersta orzeka: w żadn
ym procesie, bez względu na to, jak jest on wyidealizowany, nie można za pomocą skończo
nej liczby operacji sprowadzić temperatury układu do temperatury zera bezwzględnego.
A
B
![]()
![]()
Wyszukiwarka
Podobne podstrony:
fizykateoria, Pomoce naukowe
Sciaga fiza 2 kolo teoria, Studia, Informatyka (PG Gdańsk), Fizyka, Materiały, Pomoce naukowe
fizyka Ikolokwium, pomoce naukowe
ściąga 80, Akademia Techniczno-Humanistyczna w Bielsku-Białej, Fizyka labolatorium, Wymagania + pomo
trening z optyki, pomoce naukowe, fizyka
gim test z Ciepła, pomoce naukowe, fizyka
C4 - Roztrzepaniec, Pomoce naukowe SGSP, Moje Dokumenty, fizyka zad
gim astronomia test, pomoce naukowe, fizyka
zmiana jednostek, pomoce naukowe, fizyka
interferencja, Pomoce naukowe, fizyka
fizyka (2 str), Pomoce naukowe, studia, fizyka
magnetostatyka, Studia, Informatyka (PG Gdańsk), Fizyka, Materiały, Pomoce naukowe
trening ruch jednostajny gim, pomoce naukowe, fizyka
stosowanie i przekształcanie wzorów, pomoce naukowe, fizyka
wzory - tabela duża, sPomoce naukowe, POMOCE NAUKOWE, fizyka
C4 - PUCHAL, Pomoce naukowe SGSP, Moje Dokumenty, fizyka zad
gim test ruch drgajacy fale, pomoce naukowe, fizyka
dynamika gim trening, pomoce naukowe, fizyka
więcej podobnych podstron