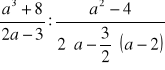Praca klasowa nr 2 - zakres rozszerzony

Funkcje wymierne

Zadanie 1

Wyznacz dziedzinę wyrażenia i zapisz je w najprostszej postaci.

1. 
   

2. 
   

Zadanie 2

Rozwiąż równanie.

1. 
   

2. 
   

Zadanie 3

Dana jest funkcja

1. Oblicz, dla jakich argumentów dana funkcja przyjmuje wartości nieujemne.

2. Przedstaw wzór tej funkcji w postaci kanonicznej.

3. Wyznacz równania asymptot wykresu tej funkcji.
   

Zadanie 4

Narysuj wykres funkcji
gdzie

1. Wyznacz zbiór wartości i miejsce zerowe funkcji g.

2. Podaj wzór funkcji g.

3. Określ liczbę rozwiązań równania:
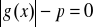
   w zależności od wartości parametru p.

Zadanie 5

Rozwiąż nierówność: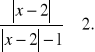

Zadanie 6

Spółdzielnia mieszkaniowa „Adrem” do ocieplenia bloku zatrudniła dwie brygady, które wykonały pracę w ciągu 12 dni. Gdyby każda brygada wykonywała pracę samodzielnie, to jedna z nich pracowałaby o 10 dni krócej niż druga. Jaką kwotę za wykonaną pracę powinna otrzymać każda z brygad tak, aby 24 000 zł, które zapłaciła spółdzielnia za wykonanie tej pracy zostały rozdzielone sprawiedliwie (proporcjonalnie do wkładu pracy)?

Model odpowiedzi i schemat oceniania pracy klasowej nr 2 - zakres rozszerzony

Maksymalna liczba punktów do zdobycia: 29 + 3

Numer zadania	Etapy rozwiązania zadania	Liczba punktów
1.	a) Wyznaczenie dziedziny wyrażenia:	1
		a) Wykonanie działań i przedstawienie wyrażenia w postaci Uwaga: Jeżeli uczeń skróci tylko jeden ze wspólnych czynników, to przyznajemy 1 punkt.	2
		b) Wyznaczenie dziedziny wyrażenia:	1
		b) Wykonanie działań i przedstawienie wyrażenia w postaci Uwaga: Jeżeli uczeń skróci tylko dwa ze wspólnych czynników, to przyznajemy 1 punkt.	2
	2.	a) Zapisanie założeń:	1
		a) Przekształcenie równania do postaci	1
		a) Rozwiązanie równania kwadratowego i podanie odpowiedzi:	1
		b) Zapisanie założeń:	1
		b) Przekształcenie równania do postaci	1
		b) Rozwiązanie równania kwadratowego i podanie odpowiedzi:	1
	3.	a) Zapisanie nierówności wraz z założeniem:	1
		a) Rozwiązanie nierówności i podanie odpowiedzi z uwzględnieniem założenia: Uwaga: Jeżeli uczeń w odpowiedzi końcowej nie uwzględni założenia, to przyznajemy 1 punkt.	2
		b) Przekształcenie wzoru funkcji do postaci kanonicznej:	1
		c) Podanie równania asymptoty pionowej:	1
		c) Podanie równania asymptoty poziomej:	1
	4.	Narysowanie wykresu funkcji	1
		a) Wyznaczenie zbioru wartości funkcji:	1
		a) Wyznaczenie miejsca zerowego funkcji g:	1
		b) Wyznaczenie wzoru funkcji g: , Uwaga: Jeżeli uczeń poda wzór funkcji bez podania dziedziny, to przyznajemy 1 punkt.	2
		c) Narysowanie wykresu funkcji	1
		c) Zapisanie odpowiedzi: 0 rozwiązań, gdy 1 rozwiązanie, gdy , 2 rozwiązania, gdy Uwaga: Jeżeli uczeń w jednym przypadku popełni błąd, to przyznajemy 1 punkt.	2
	5.	Zastosowanie definicji wartości bezwzględnej i zapisanie nierówności w postaci: dla lub dla	1
		Rozwiązanie każdej z nierówności i podanie odpowiedzi: Uwaga: Jeżeli uczeń, rozwiązując nierówności, popełni jeden błąd, to przyznajemy 1 punkt. Uczeń może rozwiązać daną nierówność inną metodą, np. podstawiając pomocniczą niewiadomą.	2
	6.	Wprowadzenie oznaczeń np.: x - czas pracy pierwszej brygady, gdyby pracę wykonywała sama, - czas pracy drugiej brygady, gdzie i ułożenie równania	1
		Rozwiązanie równania:	1
		Uwzględnienie założeń i obliczenie kwoty, jaką powinna otrzymać każda brygada: 9600 zł i 14 400 zł. Uwaga: Jeżeli uczeń, wprowadzając oznaczenia, nie zapisze założeń, ale odrzuci rozwiązanie , to otrzymuje za rozwiązanie zadania maksymalną liczbę punktów	1

Przykładowa ocena pracy klasowej

Liczba x uzyskanych punktów
Ocena	1	2	3	4	5	6
Maksymalna liczba punktów: 29 + 3

Autorzy:

Agnieszka Kamińska

Dorota Ponczek

---