
POLITECHNIKA LUBELSKA
WYDZIAŁ ELEKTRYCZNY
Nazwiska i imiona studentów : Jezierski Krzysztof Karpiuk Marcin Kolasik Mariusz
|
Symbol grupy ED. 3.4 |
||||||
Data wyk. Ćwiczenia
|
Symbol ćwiczenia
3
|
Temat zadania : Obwody prądu przemiennego z elementami ferromagnetycznymi . |
|||||
|
ZALICZENIE |
|
|
Ocena |
Data |
Podpis |
|
Cel ćwiczenia : Celem ćwiczenia jest zbadanie układów zawierających elementy ferromagnetyczne takie jak cewka z rdzeniem ferromagnetycznym .
Schemat układu do badania dławika.
Tabela pomiarów do podpunktu 3.1
Lp. |
I |
UL |
P |
cosϕ |
S |
Q |
Z |
L |
sinϕ |
|
A |
V |
W |
- |
V⋅A |
V⋅Ar |
Ω |
H |
- |
1 |
1 |
80 |
10 |
0,125 |
80 |
79,3 |
80 |
0,253 |
0,9922 |
2 |
2 |
144 |
32,5 |
0,113 |
288 |
286,16 |
72 |
0,228 |
0,9936 |
3 |
3 |
180 |
60 |
0,111 |
540 |
536,66 |
60 |
0,190 |
0,9938 |
4 |
4 |
200 |
70 |
0,088 |
800 |
796,93 |
50 |
0,159 |
0,9962 |
5 |
5 |
216 |
90 |
0,083 |
1080 |
1076,24 |
43,2 |
0,137 |
0,9965 |
6 |
5,5 |
220 |
100 |
0,083 |
1210 |
1205,86 |
40 |
0,127 |
0,9966 |
W celu wypełnienia tabeli dokonałem następujących obliczeń korzystając z poniższych wzorów :
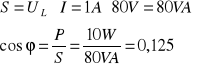
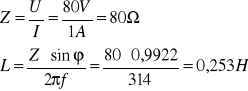
![]()
Przykładowe obliczenia zostały przeprowadzone dla pomiaru pierwszego .
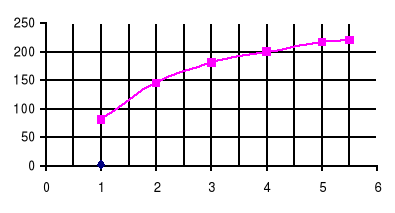
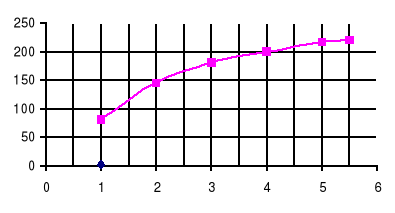
U=f(I)
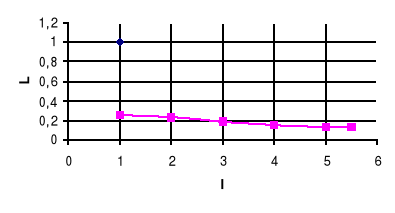
L=(I)
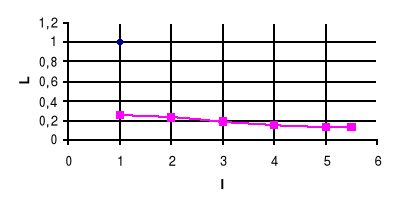
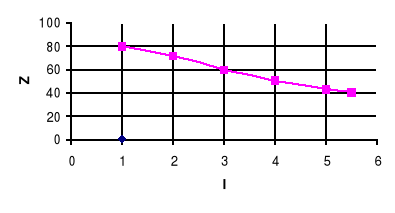
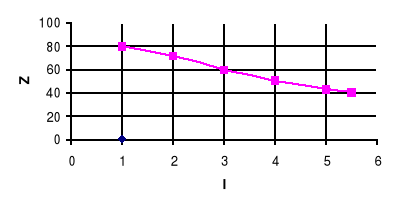
Z=f(I)
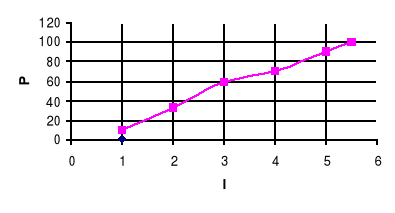
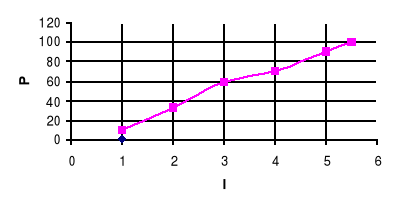
P=f(I)
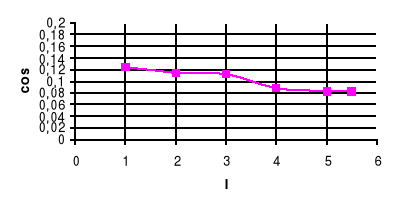
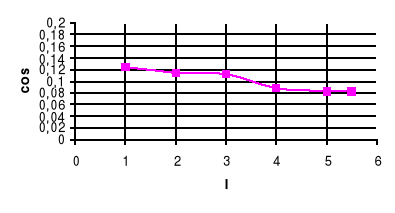
cosϕ=f(I)
Badanie zjawiska ferro rezonansu napięć.
Schemat układu do badania rezonansu napięć .
Tabela pomiarów wykonanych do podpunktu 3.3
Lp. |
I |
U |
UC |
URL |
P |
ϕ |
|
A |
V |
V |
V |
W |
° |
1 |
1 |
28 |
55 |
80 |
10 |
69 |
2 |
1,5 |
34 |
86 |
116 |
25 |
60,6 |
3 |
1,7 |
35 |
95 |
128 |
30 |
59,7 |
4 |
4,3 |
40 |
237 |
200 |
90 |
58,4 |
5 |
4,95 |
60 |
270 |
210 |
105 |
69,3 |
6 |
5 |
63 |
300 |
215 |
105 |
65,3 |
7 |
4,5 |
46 |
250 |
200 |
95 |
62,7 |
8 |
4 |
30 |
220 |
196 |
85 |
45 |
9 |
3,5 |
22 |
195 |
188 |
75 |
13 |
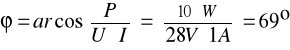
Badanie zjawiska ferro rezonansu prądów .
Schemat układu do badania rezonansu prądów .
Tabela pomiarów do podpunktu 3.4
Lp. |
U |
I |
IC |
IL |
P |
ϕ |
|
V |
A |
A |
A |
A |
° |
1 |
125 |
0,33 |
1,7 |
1,9 |
25 |
52,7 |
2 |
130 |
0,32 |
2 |
2,1 |
35 |
32,7 |
3 |
140 |
0,32 |
1,95 |
2,1 |
35 |
38,6 |
4 |
150 |
0,32 |
2,15 |
2,25 |
40 |
33,5 |
5 |
160 |
0,335 |
2,38 |
2,4 |
45 |
32,9 |
6 |
170 |
0,37 |
2,65 |
2,56 |
52 |
34,2 |
7 |
175 |
0,45 |
2,9 |
2,7 |
58 |
42,5 |
8 |
200 |
1,2 |
4,1 |
3,12 |
80 |
70,5 |
9 |
210 |
1,75 |
4,85 |
3,45 |
94 |
75,2 |
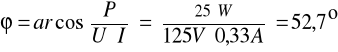
Wykresy do tabel 3,3 i 3,4 dołączone są na papierze milimetrowym.
Wnioski
Na podstawie dokonanych pomiarów i obliczeń można powiedzieć , że badany element w podpunkcie 3.2.1 jest elementem nieliniowym . Takie twierdzenie można oprzeć na fakcie iż impedancja badanego elementu zmienia się wraz z ze zmianą napięcia zasilającego . Przy niskiej wartości napięcia zasilającego układ nie wykazywał cech indukcyjnych badanego elementu , i dopiero po wzroście napięcia zasilającego do takiej wartości , że było możliwe odczytanie mocy pobieranej przez układ można było wyznaczyć wartość indukcyjności badanego układu . Brak wartości indukcyjności cewki we wcześniejszych pomiarach wynika z zerowej wartości odczytanej mocy pobieranej przez układ .
W układ 3.2.2 służył do badania zjawiska ferro rezonansu napięć . Badany układ wykazywał charakter indukcyjny do wartości prądu około 0,5A i 50V , a powyżej tej wartości charakter pojemnościowy .
W układ 3.2.3 posłużył do zbadania zjawiska ferro rezonansu prądów . Badany układ w obszarze dokonywanych pomiarów zachowywał charakter pojemnościowy i dopiero przy ostatnim pomiarze napięcia na kondensatorze i cewce były sobie prawie równe . Na tej podstawie można sądzić , że w dalszym obszarze układ zaczął wykazywać charakter pojemnościowy .
W oby powyższych przypadkach wyniki otrzymane doświadczalne różnią się od teoretycznych założeń powyższych układów . Niedokładności te wynikają z faktu , że użyte elementy nie są elementami idealnymi , a pomiary wykonane podczas wykonania ćwiczenia są obarczone niedokładnościami przyrządów pomiarowych .
6
3
Wyszukiwarka
Podobne podstrony:
zasady metod, 2 rok, biochemia, G biochemia, Biochemia, sciagi good
tłuszcze, 2 rok, biochemia, G biochemia, Biochemia, sciagi good
sciag ng, 2 rok, biochemia, G biochemia, Biochemia, sciagi good
węglowodany pytania, Medycyna ŚUM, Rok 2, Biochemia, Kolokwia, 5 Węglowodany
6 integracja metabolizmu, Płyta farmacja Poznań, II rok, biochemia
biochemia I koło wykładowe, 2 rok, Biochemia
Zagadnienia dla BN, biotechnologia 2 sem rok2, pobrane z góry DS 7, II rok, Biochemia, Biochemia
węglowodany opracowanie, Medycyna ŚUM, Rok 2, Biochemia, Kolokwia, 5 Węglowodany
PAKIET WETA ZIMA 20142014, weterynaria uwm II rok, biochemia
SEM-15WF2011 - Metabolizm nukleotydow pur i pyr, Studia, I semestr II rok, Biochemia, Różne
2012 I termin, medycyna, II rok, biochemia, giełdy
Wykład z ćwiczeń - 21.01.2011 (piątek) mgr A. Szczepanek, UJK.Fizjoterapia, - Notatki - Rok I -, Bio
AMINOKWASY, dokumenty, farmacja 3 rok, biochemia, inne przydatne
więcej podobnych podstron