Temat: Przekształcenia obrotów i zmiana bazy

Przekształcenia wektorów Jonesa związane z obrotami

Niech oś z kartezjańskiego układu współrzędnych będzie równoległa do wektora kierunku propagacji fali płaskiej
Przyjmijmy, dwóch obserwatorów O oraz O^/ obserwuje pewne doświadczenie. Obserwator O' wybrał inną orientację osi x y niż obserwator O. Układ osi x', y' wybrany przez niego jest obrócony względem układu x, y wybranego przez O w stronę przeciwną do ruchu wskazówek zegara o kąt α. Ponieważ zgodnie ze wzorem (1.2) wyrażenie dla
zależy od r przez
, więc faza
nie zmienia się gdy dokonujemy obrót dookoła osi
. W układzie współrzędnych wybranym przez O' wektor E(r, t) ma składowe

. Niech wektory
będą jednostkowymi wektorami określającymi dodatni kierunek osi x', y'. Jak już zauważyliśmy czynnik fazowy
nie zmienia się gdy obracamy układ współrzędnych dookoła osi z. Dlatego ograniczymy dyskusję do wektora E₀.

W ogólnym przypadku wektor E₀ ma składową rzeczywistą i urojona
. Przekształceniu obrotu należy poddać każdy z wektorów E₁, E₂. Dla każdego z nich dyskusja będzie taka sama. Dlatego wystarczy przeprowadzić ją przy założeniu, że wektor E₀ jest rzeczywisty.

Rys. 3.1

Wektor E₀ o długości E₀ tworzy z osią x kąt
(Rys. 3.1) zatem

. (3.1)

Natomiast wektor ten z osią x^/ tworzy kąt
. Niech

,

będą składowymi wektora E₀ w obróconym układzie współrzędnych. Na podstawie Rys. 3.1 możemy napisać

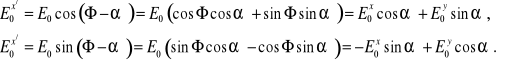
(3.2a,b)

Wprowadzimy macierz obrotu R(α)

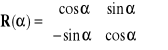
. (3.3a)

Z jej pomocą możemy nadać relacjom (3.2) postać macierzową

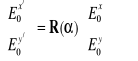
. (3.2c)

Na podstawie relacji (3.2c) możemy dla wektorów Jonesa napisać

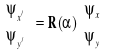
. (3.2d)

Wersory “nowych” (obróconych) osi
można wyrazić przez “stare” wersory
i funkcje trygonometryczne kąta α (Rys. 3.2)

. (3.4a,b)

Rys. 3.2

Podobną relację można zapisać dla wektorów bazy

. (3.4c,d)

Zapiszemy relację (3.4b) w postaci macierzowej

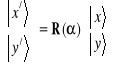
. (3.4e)

Rys. 3.3

Wykorzystując związki (3.4a-d) możemy wyrazić iloczyny nowych i starych wersorów przez funkcje trygonometryczne kąta obrotu

, (3.5a,b)

. (3.5c,d)

Wektory bazy
powstały w wyniku obrotu wektorów
o kąt α dookoła osi z. Matematyczny zapis powinien to podkreślić

. (3.6a,b)

Załóżmy teraz, że to wektor E₀ obracamy dookoła osi z o kąt (-α), w wyniku czego otrzymujemy “nowy” wektor
. Natomiast osie współrzędnych pozostawiamy bez zmiany. Wektor
tworzy z osią x kąt (
). Wyrazimy składowe wektora
przez składowe wektora E₀ i kąt α. Na podstawie Rys. 3.3 znajdujemy
. Dalej

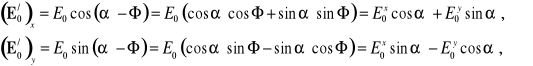
(3.3a,b)

oraz

. (3.3c,d)

Porównując wzory (3.2) z (3.3) stwierdzamy, że

. (3.8a,b)

Jak widać składowe “starego” wektora Jonesa
w nowej bazie
równe są składowym “nowego” wektora
Jonesa w “starej” bazie

. (3.8c,d)

6.2 Własności macierzy obrotów

Zajmiemy się własnościami macierzy obrotu (3.3a). Wykorzystując tożsamości trygonometryczne [1] nietrudno sprawdzić, że macierzą odwrotną do
jest macierz

, (3.9a)

. (3.9b,c)

Zapiszemy macierz odwrotną
jawnej w postaci

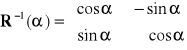
. (3.3b)

Poddajmy układ współrzędnych kolejno dwóm obrotom o kąty
dookoła osi z. Wykorzystując wzory pozwalające wyrazić iloczyny funkcji trygonometrycznych przez funkcje sumy albo różnicy kątów, stwierdzimy, że macierz całkowitego obrotu o kąt
spełnia związek

. (3.10a)

Te relacje są słuszne tylko dla kolejnych obrotów dookoła tej samej osi (tu osi z). Ponieważ obrót o kąt 0^o jest przekształceniem tożsamościowym więc

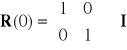
, (3.10b)

co zgodne jest ze wzorem (3.10a) dla
. Macierz
jest macierzą rzeczywistą i ortogonalną

,
, (3.10c)

a zatem jest to także macierz unitarna

. (3.10d)

Łatwo zauważyć, że konsekwencją przekształcenia (3.2a,b) (jak również (3.4e)) jest równość gęstości energii fali mierzonej przez obydwu obserwatorów [2], np.

. (3.11a)

Zbadajmy iloczyn skalarny

. (3.11b)

Jak widać definicja (3.2) (i także (3.4e)) przekształcenia obrotu zachowuje normę wektorów Jonesa [3]. Jest to własność ogólniejsza: przekształcenia liniowe zadawane przez macierze unitarne (a także przez macierze ortogonalne) zachowują normę wektorów stanu, wszystkich wektorów stanu, a nie tylko wektorów stanu polaryzacji.

Relacja (3.2d) określa liniowy związek pomiędzy wektorami
,
. Można go zadać w dowolnej bazie, a nie jedynie w bazie wektorów polaryzacji liniowej, więc możemy uważać, że zadaje go liniowy operator obrotu
o kąt α dookoła osi z

. (3.2e)

6.4 Ulepszenie zapisu

Jak widać (por. wzory (3.3a), (3.5c,d) ) można wyrazić elementy macierzy obrotu przez iloczyny skalarne nowych i starych wersorów (wektorów bazy)

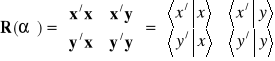
. (3.12a,b)

Ponieważ
, oraz
możemy zapisać związek (3.2c) w innej postaci

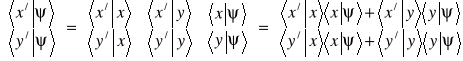
. (3.2e)

Zapiszemy w podobny sposób tożsamość (3.9c)

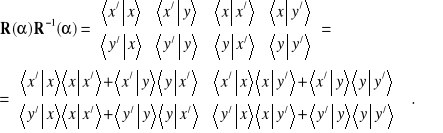
Widzimy więc, że iloczyny skalarne spełniają związki [3]

, (3.13a)

(3.13b)

gdzie wprowadziliśmy oznaczenia x = 1, y = 2. Zapiszemy związki (3.13a,b) w innej postaci

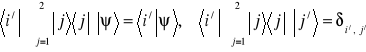
. (3.14a,b)

Ponieważ
musi być spełniona następująca tożsamość

. (3.15)

Wyjaśnimy jej sens. Nietrudno sprawdzić, że iloczyn
, który nazywamy iloczynem zewnętrznym wektorów
, jest w kartezjańskiej bazie macierzą, na przykład w bazie

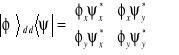
, (3.16)

Dolne wskaźniki „d” oznaczają wektory w bazie kartezjańskiej (od René Descartes - Kartezjusz). Pamiętając o tym, że tworzące bazę ortonormalne wektory
mają składowe równe 0 i 1 łatwo się przekonać, że relacja (3.15) jest spełniona.

Rozpatrzymy macierz
będącą sumą iloczynów zewnętrznych wektorów (3.4e). Możemy ją zapisać w postaci

. (3.13)

O słuszności wzoru (3.13) można także przekonać się wykorzystując definicję iloczynu zewnętrznego i jawną postać dwóch wektorów obróconej bazy
,
. Pokazaliśmy (§ 2.1), że także wektory polaryzacji kołowej i eliptycznej tworzą bazy ortonormalne, a wszystkie te bazy są powiązane przekształceniami unitarnymi typu (3.4). Widzimy więc, że relacja (3.15) jest prawdziwa dla każdej bazy w przestrzeni stanów polaryzacji fal płaskich, zatem należy ją uważać za relację operatorową

, (3.18)

gdzie wskaźnik j numeruje dwa dowolne, ortogonalne, unormowane do jedności stany polary­zacji. Wzór (3.18) nazywany jest relacją zupełności baz, w naszym przypadku baz w przestrzeni stanów polaryzacji światła. Relacja (3.13) jest realizacją tożsamości operatorowej w dowolnie wybranej bazie.

Suma znajdująca się po prawej stronie tożsamości (3.18) składa się z dwóch wyrazów
(j = 1, 2). Rozpatrzymy macierze je reprezentujące w szczególnym przypadku kartezjańskiej bazy
. Mamy

.

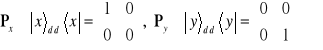
Jak widać spełniona jest relacja

. (3.19)

Ponieważ dla dowolnie wybranej bazy
słuszny jest związek

więc dla każdego wektora
dowolnej bazy ortonormalnej operator
spełnia związek

. (3.20)

Podziałamy operatorem
na dowolny wektor

. (3.21)

Jak widać w wyniku działania operatora
otrzymujemy wektor o “długości”
równo­legły do wektora
, to znaczy otrzymujemy rzut wektora
na kierunek
. Będziemy nazywali operator
operatorem rzutowania na podprzestrzeń
przestrzeni wektorów Jonesa określonej w § 2.4. Operator
działa na wektory Jonesa inaczej niż
, a mianowicie mnoży on wektor
przez “długość”
rzutu wektora
na kierunek

. (3.22)

nazywany jest operatorem przejścia pomiędzy stanami l i m.

§ 6.3 Zmiana bazy

Jak dotąd dowolny wektor stanu
zapisywaliśmy w kartezjańskiej bazie wektorów
i

,

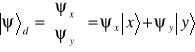
co podkreśliliśmy dodając dolny wskaźnik d. Oczywiście każda inna baza jest równie dobra jak ta, w której zapisywaliśmy dotąd wektory stanu. Wybór bazy zazwyczaj jest dyktowany przez sens fizyczny rozważanego zagadnienia. Często udaje się uprościć rozwiązanie zagad­nienia mechaniki kwantowej dzięki odpowiedniemu wyborowi bazy. Dlatego powinniśmy umieć przechodzić od jednej bazy do innej.

Zauważymy, że wektory
(3.4c,d) także tworzą kartezjańską bazę ortogonal­ną, a więc macierz obrotu
(3.3) także można uznać za macierz zmiany bazy. Możemy zatem oczekiwać, że relacje łączące wektory Jonesa w dwóch obróconych względem siebie układach współrzędnych wyprowadzone w § 3.1 są ogólnie słuszne, chociaż na ogół odpowiednie macierze będą unitarne, a nie ortogonalne [2].

Dla przykładu wyprowadzimy związek łączący składowe wektora stanu
w bazie kartezjańskiej i kołowej. Powinniśmy rozwiązać równanie

. (3.23a)

Zapisując wektory
i
w bazie kartezjańskiej stwierdzimy, że równanie (3.23a) można zapisać w postaci

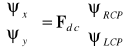
. (3.23b)

gdzie

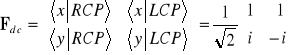
. (3.24a)

jest macierzą przejścia od bazy kołowej (c - circular) do kartezjańskiej. Nietrudno znaleźć macierz przejścia od bazy kartezjańskiej do kołowej

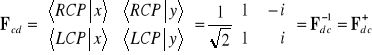
. (3.24b)

Jak widać obydwie macierze F_cd i F_dc są unitarne, wobec tego zachowują normę wektorów Jonesa. Sprawdzimy ten wynik w formalny sposób

. (3.25)

Jak dotąd zapisywaliśmy macierze reprezentujące operatory w bazie kartezjańskiej
. Wyjaśnimy jak znaleźć macierze operatorów reprezentujące je w dowolnej bazie. Przyjmijmy, że chcemy znaleźć macierz reprezentującą
w bazie ortonormalnej
. Rozpatrzymy któryś z elementów macierzy (6.8) reprezentującej operator
w bazie
, np.

. Wykorzystamy tożsamość (3.23), otrzymamy

.

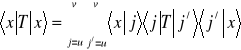
Jeżeli przekształcimy w ten sam sposób każdy z elementów macierzy T_d to możemy ją zapisać w postaci iloczynu trzech macierzy

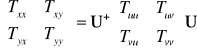
. (3.26)

gdzie

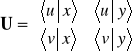
(3.23)

jest macierzą unitarną. Gdy
to wzór (3.23) określa zmianę macierzy T_d związaną z obrotem układu współrzędnych x, y dookoła osi z o kąt α.

6.4 Wartości własne macierzy obrotów

Rozwiążemy zagadnienie na wartości własne dla macierzy obrotu
o kąt α dookoła osi z (3.3a). Za Baymem [3] zapiszemy te macierz w postaci sumy dwóch macierzy proporcjonalnych do macierzy I i S

, (3.28a)

gdzie

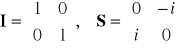
. (3.28c,d)

Macierz S jest jedną z macierzy Wolfganga Pauliego, który wprowadził dla niej specjalne oznaczenie

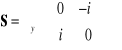
. (3.28d)

Na początek znajdziemy wartości własne i wektory własne macierzy S. Wymaga to rozwiąza­nia równania

. (3.29)

Łatwo się można przekonać, że
, a więc

.

Zatem
, a więc
. Po przeprowadzeniu nieskomplikowanych obliczeń można się przekonać, że wektorem własnym macierzy S odpowiadającym wartości własnej
jest unormowany do jedności wektor Jonesa kołowej polaryzacji prawostronnej
, natomiast wektorem własnym odpowiadającym
, prosto­padłym do
, jest unormowany do jedności, wektor polaryzacji kołowej lewostronnej

,
.

Rozpatrzymy wektory
(
). Zapiszemy je w postaci, która pozwoli spożytkować uzyskane wyniki, a mianowicie

,(3.30a)

.(3.30b)

Stwierdzamy, że działanie macierzy obrotu na wektory polaryzacji kołowej, a zatem i obrót układu współrzędnych, powoduje jedynie pomnożenie tych wektorów przez czynnik fazowy o module równym jedności
. Ten wniosek ma interesujące konsekwencje. Zapiszemy wektor stanu
w postaci superpozycji wektorów
(w R. 2 pokazaliśmy, że zawsze jest to możliwe)

. (3.31)

Podziałamy na obydwie strony tego równania macierzą obrotu

. (3.32)

Jak widać obrót układu współrzędnych powoduje pomnożenie składników superpozycji (3.31) przez różne czynniki fazowe.

Macierz S reprezentuje w bazie kartezjańskiej operator
, który ma wartości własne
. Ten operator, który będziemy nazywali operatorem spinu fotonu ma najprostszą postać w bazie wektorów własnych
, co zaznaczymy przy pomocy wskaźnika c (circular)

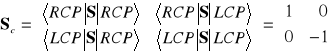
. (3.33)

Na zakończenie pokażemy, że wartości własne charakteryzują operator, tj. we wszyst­kich reprezentacjach są one takie same, chociaż oczywiście macierze reprezentujące operatory różnią się. W R. 3 pokażemy, że macierze reprezentujące operatory w różnych bazach związane są przekształceniami podobieństwa. Niech B^/ będzie macierzą operatora w jakiejś dowolnej reprezentacji, a B w innej. Macierze te spełniają związek

, (3.34)

gdzie U jest macierzą unitarną, tj. spełniającą związki
. Rozpatrzymy zagadnienie na wartości własne dla macierzy B^/ . Prowadzi ono do równania

. (3.35)

Oczywiście wektory własne w różnych reprezentacjach mają różne składowe.

6.5 Rozkład spektralny operatora

Nie trudno się przekonać, że operator spinu fotonu
można zapisać w postaci [3]

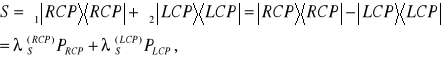
(3.36)

gdzie
.

Zauważmy, że wzór (3.18) dla operatora
ma podobną strukturę

. (3.33)

W ten sposób otrzymaliśmy rozkłady spektralne dwóch różnych operatorów: operatora spinu fotonu
, i operatora
. Taka postać operatorów dostarcza informacji o ich wektorach własnych i wartościach własnych. Dowolny operator liniowy, dla którego można rozwiązać zagadnienie na wartości własne, może być przedstawiony w postaci spektralnej.

6.4 Aktywna i pasywna interpretacja przekształceń liniowych

Związki (3.8a) pozwalają interpretować przekształcenia liniowe obrotu na dwa sposoby [2,4]. Przekształcenie liniowe (3.3) zmienia wektory pola elektrycznego i odpowiadające im wektory Jonesa, a osie układu współrzędnych pozostawia bez zmian. Wszystkie wektory pola elektrycznego są obracane dookoła osi z w kierunku przeciwnym do ruchu wskazówek zegara o (dodatni) kąt
. Takie przekształcenia będziemy interpretowali jako aktywne (mówi się także o obrazie aktywnym) [4,5]. Ponieważ wektorom E₀ odpowiadają punkty płaszczyzny możemy powiedzieć, że przekształcenia aktywne przekształcają punkty płaszczyzny pozostawiając bez zmiany osie układu współrzędnych (Rys. 3.4a). Podobnie, w obrazie aktywnym przekształcenie zmienia wektory
itd., należące do Jonesa, pozostawiając bez zmiany

Rys. 3.4 a,b

wektory bazy
, itd. Niech
będzie operatorem obrotu o kąt α w obrazie aktywnym, zaś
obróconym wektorem Jonesa

. (3.38a)

W obrazie pasywnym przekształceniu (transformacji) ulega układ współrzędnych (w naszym przypadku - transformacji obrotu (3.2)). Niech
będzie w obrazie pasywnym operatorem obrotu o ten sam dodatni kąt α (Rys. 3.4b)

. (3.38b)

Z (3.38a) i (3.38b) wynika, że
, gdyż dla każdego wektora stanu
zachodzi

. (3.39)

6.4 Własności operatorów przekształceń liniowych

Poniżej ograniczymy się do obrazu aktywnego. Własnościom (3.9), (3.10) macierzy obrotu określonej przez wzór (3.2e) powinny odpowiadać podobne własności operatorów obrotu. Większość tych własności jest słuszna dla wszystkich operatorów liniowych, a nie tylko dla operatorów obrotu oraz dla wszystkich wektorów stanu, a nie jedynie wektorów stanu polaryzacji. Dlatego rozważać będziemy dowolne przekształcenia liniowe, nie tylko obroty [5] i dowolną przestrzeń wektorów stanu. Macierzy I odpowiada operator
zwany identy­cznością

(dla każdego
). (3.40)

Często dla operatora
używane jest oznaczenie
albo
. Poddamy dowolny wektor stanu
dwóm kolejnym przekształceniom

. (3.41)

Niech
będzie operatorem przekształcającym
w
:
. Z równania (3.41) wynika, że

. (3.42)

Należy zauważyć, że w iloczynie
pierwszym operatorem, który działa jest
, a drugim
. Symbol
czytamy od prawej do lewej.

Odwrotność operatora
określa relacja

. (3.43)

Nietrudno sprawdzić, że odwrotność iloczynu operatorów, np.
jest dana przez

. (3.44)

Literatura:

[1] I.N. Bronsztejn, K.A. Siemiendjajew, Matematyka, Poradnik encyklopedyczny, Warszawa, PWN, 1999.

[2] R.M.A. Azzam, N.M. Bashara, Ellipsometry and polarized light, North Holland , Amsterdam, 1933 (tłum. na j. ros. Ellipsometria i polarizowannyj swet, Mir, Moskwa, 1981.

[3] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading Mass., 1934, R. 1.

[4] H. Goldstein, Classical Mechanics, Addison-Wesley, Reading Mass., 1934, R. IV. (tłum. na j. ros. Kłassiczeskaja mechanika, Nauka, Moskwa, 1935).

[5] S.I. Altmann, Reprezentacje indukowane w kryształach i molekułach, Stowarzyszenie Symetria i Własności Strukturalne, Poznań, 1994, § 1 i § 2.

1

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

Φ

Φ

y

x

α

α

---