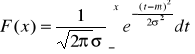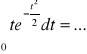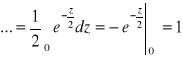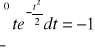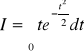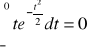WARIANCJA ZMIENNEJ LOSOWEJ - c.d.

Tw:
.

dow:

.

Wariancje w Poszczególnych rozkładach:

1. X - rozkład Bernoulliego
   ,
   

/
/

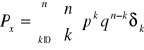
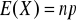
2. X - rozkład Poissona
   ,
   

/
/

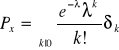
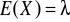
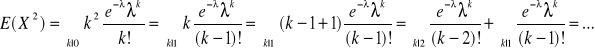
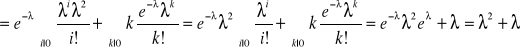
Tw:
.

Funkcja
przyjmuje wartość najmniejszą jeżeli
.

dow:

najmniejsze ⇔
⇔
.

Tw: (Nierówność Czebyszewa )

Jeżeli zm. los. X posiada
oraz
, to
.

dow:

na

, czyli

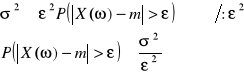
np.: k - liczba zajść zdarzenia A w serii n doświadczeń (k - zmienna losowa) wg. Schematu Bernoulliego

częstość wystąpienia zdarzenia A (nowa zmienna losowa).

lub

Rzucamy 1000 razy monetą i otrzymujemy k-razy orła. Z jakim co najmniej prawdopodobieństwem można twierdzić, że będzie spełniona nierówność:

/
,
,

Uwaga! Oszacowanie jest niedokładne.

Rozkład normalny:

Def: Mówimy, ze zmienna losowa X ma rozkład normalny o parametrach m i
jeżeli ma rozkład ciągły o funkcji gestości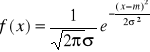

. Zapisujemy wówczas:
.

Uwaga:
całka nieelementarna

Ale: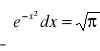
,
,
.

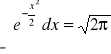
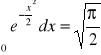
Sprawdzamy, że
jest gęstością:

/
/

	- punkty przegięcia
		odczytujemy z tablic

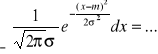
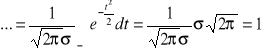
Tw: Jeżeli X ma rozkład normalny
, to zmienna losowa
też ma rozkład normalny
.

dow:

Y też ma rozkład normalny - dowód później.

dowód:

/
/

/ / +

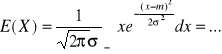
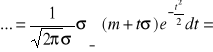
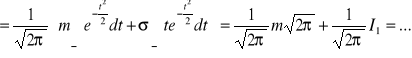
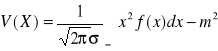
3

Luke Rachunek prawdopodobieństwa-wykład 9.4.2k+1

---