ALGORYTMY REGULACJI ADAPTACYJNEJ

Istota regulacji adaptacyjnej polega na automatycznym dopasowywaniu parametrów regulatora do zmieniających się właściwości obiektu regulacji i jego otoczenia, tak aby zapewnić pożądane cechy układu regulacji. W szczególności chodzi o zapewnienie:

- stabilnej pracy układu regulacji;

- odporności stabilności, tzn. niezależności stabilności od spełnienia założeń dotyczących struktury modelu obiektu, poczynionych na etapie syntezy regulatora;

- pożądanych charakterystyk tłumienia zakłóceń oddziaływujących na wielkość regulowaną;

- pożądanych charakterystyk nadążania wielkości regulowanej za wielkością zadaną;

- niewrażliwości wymienionych cech na zmiany właściwości dynamicznych obiektu regulacji.

Zmiany właściwości dynamicznych obiektów regulacji wynikają z tego, że procesy przemysłowe z natury są niestacjonarne, nieliniowe i często pracują w warunkach silnych zakłóceń losowych. Błędne założenia co do struktury modeli obiektów są wynikiem chęci stosowania przez projektujących modeli maksymalnie uproszczonych.

Każdy poprawnie zaprojektowany układ regulacji, dzięki ujemnemu sprzężeniu zwrotnemu, odznacza się pewną naturalną odpornością na błędy struktury i zmiany parametrów modelu obiektu. Wszystkie zmiany wielkości regulowanej są kompensowane bez względu na ich źródło pochodzenia, gdyż są one interpretowane jako zakłócenia wyjścia obiektu. Kompensacyjne możliwości sprzężenia zwrotnego są jednak ograniczone i w przypadku dużych zakresów wahań struktury, parametrów i zakłóceń, układ może nie spełniać nawet warunku stabilności. Konieczne jest więc przestrajanie on-line algorytmu regulatora (ręczne lub automatyczne) w trakcie funkcjonowania układu - czyli zastosowanie adaptacji.

Idea regulacji adaptacyjnej może być realizowana na wiele sposobów. Rozróżnia się dwie główne grupy realizacji, wykorzystujące:

1. programowe zmiany parametrów algorytmu regulatora,

2. identyfikację modelu (obiektu lub regulatora ).

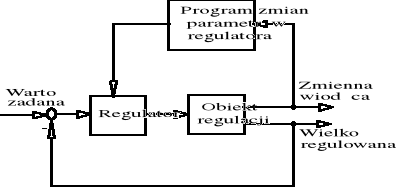
Ad. 1 Istota regulacji polega tutaj na stałym uzależnianiu parametrów regulatora od tzw. zmiennej wiodącej tzn. pomiarowo dostępnej zmiennej, charakteryzującej bieżące właściwości obiektu. Taką zmienną może być np. czas, natężenie produkcji itp. Parametrem regulatora, który najczęściej jest programowany jest wzmocnienie (ang. gain scheduling). Schemat blokowy tej prostej strategii adaptacji przedstawia rys.1.

Rys. 1. Schemat blokowy realizacji adaptacji „gain scheduling”

Ad. 2

Dla układu regulacji adaptacyjnej z identyfikacja modelu (patrz rys. 2), parametry regulatora (też struktura), wyznaczane są na podstawie wyników pomiarów wejść i wyjść obiektu regulacji i bieżącej identyfikacji modelu parametrycznego (ang. self tunning).

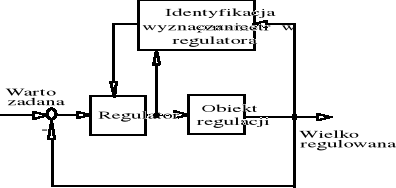
Rys. 2. Schemat blokowy struktury realizacji algorytmu adaptacji z bieżącą identyfikacją modelu

Zaletą takiego rozwiązania jest uniwersalność, wadą - bardzo duża złożoność teoretyczna, powodująca konieczność szerokiego stosowania komputerowych technik symulacyjnych do analizy i projektowania tego typu układów.

Z istnienia dwóch odrębnych możliwości identyfikacji modelu, wynika podział na pośrednią i bezpośrednią regulację adaptacyjną. Jeżeli identyfikowanym modelem jest model obiektu i na jego podstawie oraz znajomości celu regulacji dokonywana jest synteza regulatora, to taką regulację nazywa się pośrednią regulacją adaptacyjną. Jeżeli identyfikowanym modelem jest model algorytmu regulatora i jego parametry uzyskuje się (estymuje) bezpośrednio z pomiarów, to mówi się o regulacji adaptacyjnej bezpośredniej.

Regulacja adaptacyjna pośrednia

Algorytm samoprzestrajający w realizacji pośredniej składa się z dwóch etapów obliczeniowych:

1. Identyfikacji on-line parametrów modelu obiektu prowadzonej z okresem
   ,

2. Syntezy nastaw algorytmu regulacji, które mogą być wyznaczane z innym okresem próbkowania.

W pierwszym i drugim etapie mogą być wykorzystywane różnorodne algorytmy i metody np. rekurencyjne wersje metod identyfikacji LS, IV, ML w odniesieniu do identyfikacji takich modeli jak ARMAX, BJ, OE itp. cyfrowe algorytmy PID, algorytmy predykcyjne, kompensacyjne, „od stanu” itd., z automatycznym doborem nastaw wg. różnorodnych kryteriów jakości regulacji (alokacja biegunów, minimum wariancji, najkrótszy czas ustalania się przebiegów „dead-beat”, LQ, LQG, itd.

Regulacja adaptacyjna bezpośrednia (przykład)

Zakłada się, że cyfrowy model instalacji przemiałowej, traktowanej jako obiekt regulacji wypełnienia młyna opisuje następujące równanie (model Boxa-Jenkinsa)

(1)

gdzie:

w(i) są wartościami wielkości regulowanej (stopnia wypełnienia młyna),

u(i) są wartościami strumienia wejściowego materiału (nadawy),

e(i) jest dyskretnym białym szumem gaussowskim o parametrach (0,λ2),

K=k+1; (k - czas opóźnienia, liczony w okresach impulsowania),

wielomiany A, B, C, D przyjmują się w następującą postać

A =
(2)

B =
(3)

C =
(4)

D =
(5)

Jako cel regulacji przyjmuje się minimalizację wariancji różnicy wielkości regulowanej i zadanej oraz ważonej sumy kwadratu wielkości sterującej, czyli optymalizację wskaźnika uogólnionego ( GMV) postaci

(6)

Przyjęty do rozwiązania problemu optymalnego nadążania wielkości sterowanej za wielkością zadaną i optymalnej kompensacji zakłóceń, samoprzestrajający się algorytm regulacji minimalnowariancyjnej powinien wykorzystywać postać modelu obiektu, dogodną do prostego i szybkiego wyznaczania na bieżąco K-krokowej predykcji wielkości sterowanej. Takie wymagania spełnia tzw. model predykcyjny, który umożliwia nieobciążoną estymację współczynników, optymalnego wg. (6) algorytmu regulacji przy pomocy metody RLS z odpowiednio dobranym doświadczalnie współczynnikiem zapominania α. Algorytm ten określony jest następującym równaniem operatorowym

(7)

gdzie nieznane wielomiany postaci

(8)

(9)

wyznacza się z równania wielomianowego

(10)

Zastępując odpowiednie wyrażenia w (7) wielomianami oznaczonymi przez M, L, R, optymalny algorytm można zapisać w skróconej formie

(11)

Stosując podstawienie

(12)

po szeregu przekształceniach, otrzymuje się model predykcyjny młyna

(13)

Model ten bezpośrednio umożliwia wyznaczenie predykcji minimalnowariancyjnej K - krokowej wypełnienia młyna "w" oraz estymatorów parametrów wielomianów algorytmu (11) określającego optymalne wartości nadawy „u” dla błędu identyfikacji określonego przez jego lewą stronę - zapisanego w postaci

(14)

gdzie

jest wektorem przeszłych sterowań oraz bieżących i przeszłych pomiarów wielkości sterowanej i wartości wielkości zadanej,

wektorem estymowanych parametrów algorytmu regulacji,

znaną, doświadczalnie dobieraną wartością odpowiedniego współczynnika wielomianu M.

Ostatecznie, minimalnowariancyjny algorytm samoprzestrajający się będzie realizowany zgodnie z ogólnym wyrażeniem

(15)

gdzie uaktualnianie ocen jego wektora parametrów realizowane będzie na podstawie aktualnego pomiaru wielkości sterowanej w(i) zgodnie z rekurencyjnym algorytmem najmniejszych kwadratów danym przez nastepujące wyrażenia:

(16)

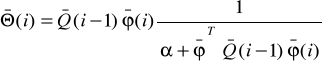
(17)

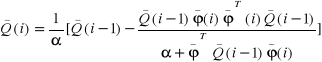
(18)

Do właściwego (w sensie zbieżności, dokładności i właściwości adaptacyjnych) działania algorytmu, wymagany jest eksperymentalny dobór współczynnika zapominania α, wagi ograniczającej sygnał sterujący β oraz współczynnika
.

ALGORYTMY SAMONASTRAJANIA (automatycznego doboru nastaw)

Automatyczny dobór nastaw jest prostą formą jednorazowej adaptacji parametrycznej regulatora do nieznanego obiektu. Jest obecnie często spotykaną funkcją nowoczesnych regulatorów mikroprocesorowych PID.

Pierwszy regulator cyfrowy z możliwością samonastrajania wprowadziła w 1981 r. firma Northrup.

Najczęściej stosowane dwie metody automatycznego doboru nastaw regulatorów PID:

• Metoda odpowiedzi skokowej (MOS),

• Metoda oscylacji wymuszonych (MOW).

Metoda odpowiedzi skokowej

Do identyfikacji obiektu wykorzystywana jest jego odpowiedź na skok sygnału wejściowego o znanej amplitudzie. Należy podać amplitudę skoku oraz czas obserwacji odpowiedzi obiektu regulacji, w ciągu którego powinna się ona ustalić. Konieczna jest więc pewna wiedza o dynamice obiektu. W chwili włączenia procedury samostrojenia sygnał wyjściowy z obiektu powinien być ustalony, w przeciwnym wypadku zarejestrowana odpowiedź skokowa nie będzie odpowiadała rzeczywistej odpowiedzi obiektu (rys. 1).

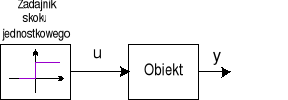
Rys. 1. Schemat blokowy układu samonastrajania metodą MOS

Najczęściej wykorzystywane transmitancje to:

,
,
,

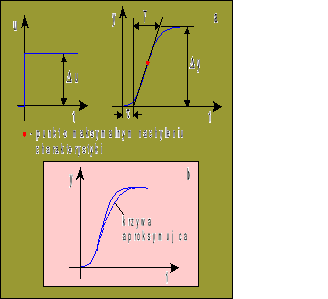
Rys. 2. Sposób wyznaczania parametrów dwóch pierwszych transmitancji

aproksymacja pozostałych (metodą najmniejszych kwadratów)

Przykładowe nastawy dla transmitancji

Metoda	Nastawy	K	Ti	Td
Ziegler-Nichols	P
		PI		3τ
		PID		2τ
	Chien-Hrones-Reswick	P
		PI		1,2T
		PID		T	0,5τ
	Cohen-Coon	P
		PI
		PID
	Imc PID	P
		PI
		PD
		PID

Algorytm MOS wymaga rozpięcia pętli sprzężenia zwrotnego na czas doboru nastaw. Kontrola nad obiektem w trakcie trwania eksperymentu jest wiec ograniczona. Jeżeli zakończenie eksperymentu uzależnione jest nie od czasu ale od chwili osiągnięcia przez sygnał stanu ustalonego, konieczne jest wprowadzenie zabezpieczenia przerywającego eksperyment po przekroczeniu dozwolonego czasu. Eksperyment musi być także przerwany jeżeli sygnał wyjściowy obiektu przekroczy granice alarmowe.

Może się zdarzyć, że fizyczna budowa obiektu sterowania pozwala na rozpięcie pętli sprzężenia dopiero po zatrzymaniu procesu, lub jest to w ogóle niemożliwe. W takim przypadku metoda MOS nie może być zastosowana.

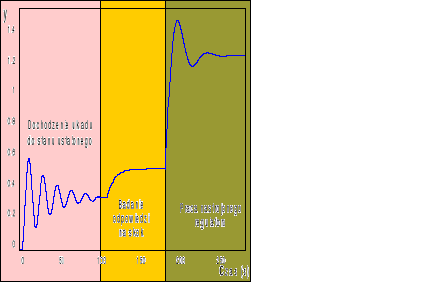
Rys. 2. Przykładowy przebieg sygnału wyj. obiektu podczas eksperymentu doboru nastaw metodą MOS

Metoda oscylacji wymuszonych

Metoda ta bazuje na spostrzeżeniu, że parametry regulatora można wyznaczyć znając punkt krytyczny charakterystyki Nyquista układu regulacji.

Początkowo metoda oscylacji wymuszonych wykorzystywała znany powszechnie klasyczny eksperyment Zieglera-Nicholsa. Taki podejście było trudne do zautomatyzowania..

Problem ten został rozwiązany przez Åströma-Häglunda, którzy zaproponowali alternatywną metodę wykorzystującą pojęcie funkcji opisującej i element przekaźnikowy.

Także w przypadku tej metody ważne jest aby rozpoczęła się ona, gdy sygnał sterowany jest w stanie ustalonym. Po załączeniu przekaźnika algorytm oczekuje na ustalenie się drgań. Dokonywany jest pomiar amplitudy pierwszej harmonicznej drgań oraz okres drgań. Na ich podstawie obliczane jest wzmocnienie krytyczne Znając wzmocnienie krytyczne i okres drgań obliczane są nastawy regulatora PID (z reguły są to nastawy Zieglera-Nicholsa lub ich modyfikacja).

Przebieg doboru nastaw metodą oscylacji wymuszonych został przedstawiony na rys. (3)

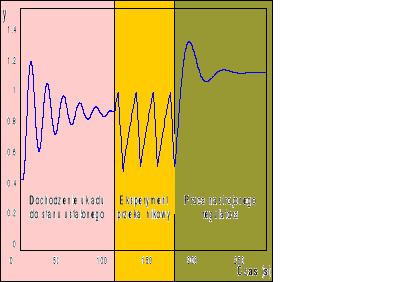
Rys. 3. Przebieg sygnału wyjściowego obiektu y podczas procesu nastrajania metodą MOW

Metoda MOW ma kilka zalet w stosunku do metody MOS. Strojenie odbywa się w pętli zamkniętej, nie ma więc praktycznie możliwości utraty stabilności przez układ. Metoda ta jest w mniejszym stopniu zależna od rodzaju identyfikowanego obiektu. Nastawy będą poprawne nawet dla bardziej złożonych obiektów, chociaż mniej dokładne jak przy użyciu metody MOS z transmitancją dobraną odpowiednio do obiektu regulacji.

W mniejszym stopniu wymagana jest kontrola nad przebiegiem strojenia. Dobrane nastawy mogą być wdrożone bez zatwierdzenia ich przez operatora.

Inne metody samonastrajania

Algorytm Exact - Foxboro

______________________________________________________________________________________

E. Żak

Wykład

n. t. NOWOCZESNE ALGORYTMY REGULACJI CYFROWEJ

8

__________________________________________________________________________________

Algorytmy adaptacyjne i samonastrajające

---