Zagadnienia do Matury Ustnej z Matematyki

(profil matematyczno - informatyczny)

1. Zasada indukcji matematycznej i jej zastosowanie.

Jeżeli twierdzenie T jest prawdziwe dla pewnej liczby naturalnej n₀, i dla każdej liczby naturalnej k ≥ n₀ prawdziwa jest implikacja: T(k) ⇒ T(k+1). Twierdzenie T jest prawdziwe dla każdej liczby naturalnej n ≥ n₀.

2. Styczna do wykresu funkcji f w punkcie o odciętej x₀.

y = f(x) A = (x₀,f(x₀))

y - f(x₀) = f'(x₀) ⋅ (x - x₀)

3. Dowód: funkcja f(x) = |x| nie jest różniczkowalna w punkcie o odciętej x₀ = 0.

Mamy wykazać, że nie istnieje pochodna funkcji f(x) = |x| w punkcie x₀ = 0.

Badamy istnienie granicy funkcji:

nie istnieje

Zatem pochodna tej funkcji w punkcie x₀ = 0 nie istnieje.

4. Twierdzenie o trzech ciągach i jego zastosowanie.

Z:
i

T:

Zastosowanie:

5. Wyprowadzanie wzorów na sumę i iloczyn pierwiastków trójmianu kwadratowego (wzory Viete'a)

Jeżeli a ≠ 0 i x₁, x₂ są pierwiastkami trójmianu y = ax²+bx+c zachodzą związki:

Dowód:

Z założenia

Dla każdej liczby x prawdziwa jest równość:

ax² + bx + c = a (x - x₁) (x - x₂)

ax² + bx + c = ax² - axx₂ - axx₁ + ax₁x₂

ax² + bx + c = ax² - a(x₁ + x₂)x + ax₁x₂

Równość ta zachodzi dla każdej wartości x wtedy i tylko wtedy, gdy współczynniki przy zmiennej x i wyrazy stałe są odpowiednio równe:

b = - a (x₁ + x₂) /:a c = a x₁x₂

6. Definicja funkcji parzystej i nieparzystej i jej zastosowanie w zadaniach.

Funkcja y = f(x) jest parzysta ⇔

Funkcja y = f(x) jest nieparzysta ⇔

7. Wzajemne położenie dwóch okręgów na płaszczyźnie.

Okręgi rozłączne zewnętrznie: Okręgi przecinające się:

|AB| > R + r |R - r| < |AB| < R + r

Okręgi rozłączne wewnętrznie: Okręgi współśrodkowe:

|AB| < |R - r| |AB| = 0

Okręgi styczne zewnętrznie: Okręgi styczne wewnętrznie:

|AB| = R + r |AB| = |R -r| > 0

8. 
   Twierdzenie sinusów i jego dowód.

Jeżeli w Δ ABC, |AB| = c ; |AC| = b ; |BC| = a

i |∢CAB|= α i |∢ABC|=β i |∢ACB|= γ to:

gdzie R to promień okręgu opisanego na Δ ABC.

Dowód:

|∢ACB| = |∢AC'B| - jako kąty wpisane w okrąg oparte na tym samym łuku.

Δ ABC' jest prostokątny bo |∢ABC'| = 90⁰ - kąt wpisany w okrąg oparty na średnicy okręgu

|AC'| = 2R

⇒ c = 2R sinγ ⇒
⇒

analogicznie
⇒

Zatem:

9. Definicja granicy ciągu.

Wykaż, że

Ustalam
> 0

⇒
⇒
, bo n ∈ N⁺

⇒

Za n₀ możemy przyjąć każdą liczbę nie mniejszą od
np. n_o =

10. Definicja pochodnej funkcji w punkcie i obliczanie pochodnej funkcji na podstawie definicji.

Jeśli funkcja jest określona w przedziale (a,b), x₀ ∈ (a,b) i istnieje skończona granica:

, to granicę tę nazywamy pochodną funkcji f w punkcie x₀ i oznaczamy symbolem f'(x₀). O funkcji, która ma pochodną punkcie x₀ mówimy, że jest różniczkowalna w tym punkcie.

Przykład:

x₀ = 2

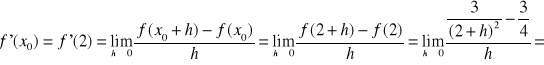
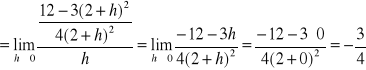
11. Definicja ciągłości funkcji w punkcie i jej zastosowanie w zadaniach.

Definicja:

Funkcję y = f(x) nazywamy ciągłą w punkcie x₀ wtedy i tylko wtedy, gdy spełnione są jednocześnie warunki:

• funkcja jest określona w punkcie x₀

• istnieje
  

• 
  

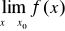
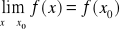
12. Twierdzenie Bezout'a w zadaniach.

Twierdzenie:

Liczba r jest pierwiastkiem wielomianu W(x) ⇔ gdy wielomian W(r) = 0 ⇔
[Q(x) jest wielomianem i W(x) = (x - r) ⋅ Q(x)]

Zadania:

1. Rozwiąż nierówność: x³-6x²+5x+12 ≥ 0

2. Liczby 2, 3 są pierwiastkami wielomianu W(x) = 2x³+mx²-13x+m. Znajdź trzeci pierwiastek.

13. Proste prostopadłe i równoległe na płaszczyźnie

Mamy dwie proste:

k: y = a₁x + b₁

l: y = a₂x + b₂

k || l ⇔ a₁ = a₂

k ⊥ l ⇔ a₁ ⋅ a₂ = -1

k : A₁x + B₁y +C₁ = 0 ,

l : Ax + By +C = 0 ,

k || l ⇔ A₁B - B₁A = 0

k ⊥ l ⇔ AA₁ + BB₁ = 0

14. Interpretacja geometryczna pochodnej funkcji w punkcie.

A = (x₀,f(x₀))

Jeśli w punkcie x₀ istnieje pochodna funkcji y = f(x) to zachodzi związek f'(x₀) = tg α, gdzie α jest kątem nachylenia do osi OX stycznej do wykresu funkcji w punkcie A = (x₀,f(x₀)).

15. Warunek prostopadłości dwóch wektorów (iloczyn skalarny).

Iloczynem skalarnym dwóch nie zerowych wektorów
i
nazywamy liczbę:

, gdzie α jest kątem między wektorami
i
.

Jeżeli
= 0 lub
= 0 to

Twierdzenie:

= [a₁,a₂]

= [b₁,b₂]

• Warunek prostopadłości wektorów
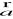
  i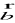
  :

Wektory nie zerowe
i
są prostopadłe wtedy i tylko wtedy, gdy ich iloczyn skalarny jest równy 0.

• Warunek równoległości wektorów
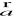
  i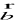
  :

Wektory nie zerowe
i
są prostopadłe wtedy i tylko wtedy, gdy:

1

B

A

A

A

A

A

B

B

B

B

A

C

B

C'

c

γ

γ

β

α

A

X₀

x

y

α

f(x₀)

---