Macierze i ich właściwości. Prawa macierzy. Rozwiązywanie układów równań liniowych. Metoda Gaussa-Jordana (pełnej eliminacji).

1. Macierze i ich właściwości.

1. Wstęp

Tablice są najczęściej używanymi strukturami zapisu danych. W matematyce noszą one nazwę macierzy - ciągów liczbowych. Jednak my często będziemy używać tablic, które nie zawierają tylko liczb, ale znaki, ciągi znaków, rekordy itd. Będą nam one pomocne w rozwiązywaniu układów równań, budowy list, sortowaniu.

Najpierw zajmiemy się matematycznymi podstawami macierzy.

Macierzą liczbową o wymiarze m×n nazywamy podwójny ciąg liczbowy {a_ik}, gdzie i przybiera wartości liczbowe i= 1, 2, 3,..., m, zaś j= 1, 2, 3, ..., n.

Macierz przedstawiamy w postaci tablicy prostokątnej o m wierszach i n kolumnach oznaczając dużą litera np.:

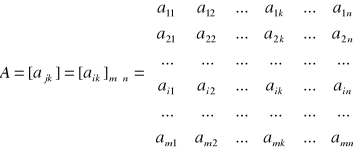
Element a_ik znajdziemy na przecięciu i-tego wiersza i k-tej kolumny, czyli pierwszy wskaźnik oznacza numer wiersza, drugi zaś numer kolumny.

Szczególnym przypadkiem macierzy jest macierz kwadratowa, tzn. taka, której wymiarem jest n×n. Nazywać ją będziemy macierzą n-tego stopnia i podobnie jak poprzednio oznaczać:

.

Macierzy kwadratowej przypisujemy liczbę zwaną wyznacznikiem macierzy:

.

Wprowadzimy teraz symbol zwany deltą Kroneckera δ_ik określany przez:

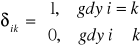
przy czym i, k są liczbami naturalnymi.

Szczególnym przypadkiem macierzy kwadratowej jest macierz diagonalna, tzn. taka, w której wszystkie elementy leżące poza główną przekątną są równe 0, czyli:

.

Możemy zapis tej macierzy uogólnić posługując się deltą Kroneckera:

.

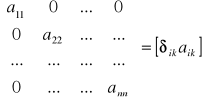
Gdy leżące na głównej przekątnej elementy są sobie równe, taką macierz nazywamy skalarną. Macierz skalarna, której elementy z głównej przekątnej są równe 1 nazywamy macierzą jednostkową:

.

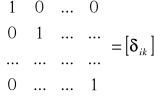
Jeśli elementy z głównej przekątnej są równe 0, czyli wszystkie elementy macierzy są zerowe, taką macierz nazywamy zerową.

Macierzą symetryczną nazywamy macierz, dla której spełniony jest warunek:

Macierzą skośnie symetryczną nazywamy macierz spełniającą warunek:

Macierz symetryczna i jednocześnie skośnie symetryczna jest macierzą zerową.

Macierz kwadratowa, której wyznacznik jest równy 0 nazywana jest macierzą osobliwą. Wynika z tego, że macierz zerowa kwadratowa jest osobliwą, ale nie każda macierz osobliwa jest zerowa np.:

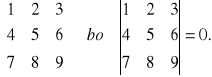
Rzędem macierzy będziemy nazywać najwyższy ze stopni macierzy kwadratowych, otrzymanych z danej dowolnej macierzy przez skreślenie pewnej liczby wierszy i kolumn, których wyznacznik jest różny od zera. Rząd macierzy zerowej jest równy zero.

rząd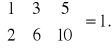

2. Działania na macierzach

Dwie macierze będziemy uważać za równe, jeśli będą miały ten sam wymiar i odpowiednio równe elementy. Równość macierzy posiada właściwości: zwrotności, symetryczności i przechodniości, dla których spełnione są odpowiednio warunki:

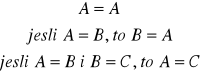
Sumą macierzy nazywać będziemy macierz o tym samym wymiarze spełniającą zależność:

,

np.:

.

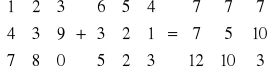
Dodawanie macierzy jest przemienne i łączne:

.

Różnicą macierzy A i B nazywać będziemy taką macierz X, która dodana do odjemnika B daje odjemną A, tzn. że X=A - B wtedy i tylko wtedy gdy B + X = A.

Wynika z tego, że:

,

np.:

.

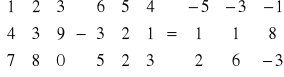
Iloczyn macierzy przez liczbę określany jest jako macierz, której każdy element jest iloczynem elementu macierz mnożonej i liczby:

,

np.:

.

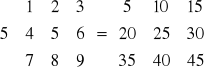
Iloczyn macierzy ma odpowiednio właściwości łączności, rozdzielności względem dodawania liczb i macierzy oraz mnożenia przez 1 i 0:

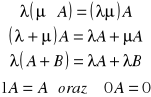
przy czym w ostatnim równaniu po prawej stronie występuje macierz zerowa (po lewej stronie występuje liczba 0).

Iloczyn macierzy A o wymiarach m×p i macierzy B o wymiarze p×n nazywamy macierz C o wymiarze m×n, której elementy c_ik powstają za pomocą elementów i-tego wiersza macierzy A i k-tej kolumny macierzy B następująco:

,

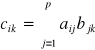
np.:

.

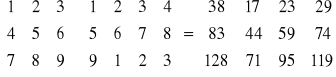
Warunkiem możliwości zachodzenia mnożenia jest równa ilość kolumn pierwszej macierzy i wierszy macierzy drugiej! Mnożenie macierzy nie jest przemienne, ale jest łączne i rozdzielne względem dodawania.

3. Droga do uzyskania macierzy odwrotnej

Tzw. macierz odwrotna będzie nam niezbędna do rozwiązywania układów równań liniowych. Aby daną macierz doprowadzić do postaci odwrotnej należy dokonać szeregu transformacji macierzy wyjściowej.

Dla przykładu weźmy macierz w postaci:

,

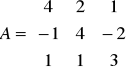
dla której przejdziemy kolejne fazy zmian.

1. Macierz minorów - macierz A^M, której poszczególne elementy wyznaczamy przez obliczanie wyznaczników tej macierzy powstałych przez skreślenie kolumny i wiersza, na których skrzyżowaniu stoi dany element.

.

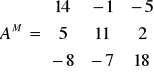
2. Macierz dopełnień - macierz A^D, powstająca wymnożenia macierzy minorów wg. wzoru:

Czyli:

.

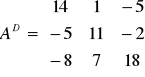
c) Macierz transponowana - jest to macierz, która powstaje przez zamianę miejscami wierszy z kolumnami i oznaczana przez A^T.

.

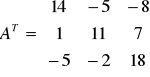
4. Macierz odwrotna - macierz A^-1, która powstaje przez wymnożenie macierzy transponowanej przez odwrotność wyznacznika macierzy wyjściowej. Otrzymujemy w ten sposób przepis na macierz odwrotną w postaci:

.

Czyli:

.

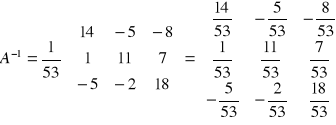
1. Rozwiązywanie układów równań liniowych.

1. Wstęp

Dany jest układ n równań liniowych z n niewiadomymi w postaci:
, gdzie:

.

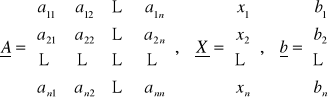
Metody rozwiązywania powyższego układu dzielimy na:

• metody wprost (Cramera, Gaussa-Jordana, Gaussa, Banachiewicza, Cholesky),

• metody iteracyjne (iteracji prostej, Seidla).

W metodach wprost uzyskuje się wynik po skończonej liczbie operacji. Jest to rozwiązanie dokładne przy zaniedbaniu błędów zaokrągleń. Metoda Cramera wykorzystywana do obliczeń analitycznych jest nieprzydatna do obliczeń numerycznych z powodu dużej liczby operacji niezbędnych do znalezienia rozwiązania (
co dla n=10 daje 359251200 operacji).

W metodach iteracyjnych otrzymuje się wynik w zbieżnym procesie iteracji. Liczba operacji nie jest z góry ustalona. Wszystkie metody iteracyjne mają proste algorytmy przez co nadają się do maszyn liczących.

1. Metoda Gaussa-Jordana (pełnej eliminacji)

Układ przedstawiamy w postaci:

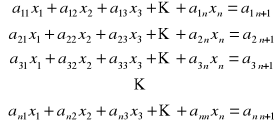
Układ można teraz przekształcić dokonując operacji na macierzy
:

Etap redukcji k=1

Krok 1

Pierwszy wiersz dzielimy przez a_11:

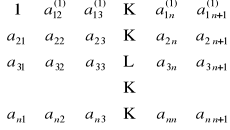
przy czym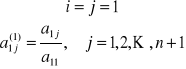

Krok 2

Od drugiego wiersza odejmuje się pierwszy pomnożony przez a_21:

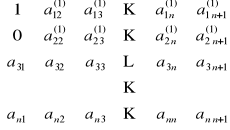
przy czym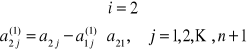

Krok 3

Od trzeciego wiersza odejmuje się pierwszy pomnożony przez a₃₁:

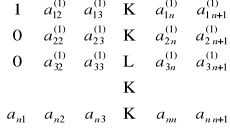
przy czym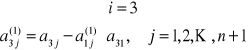

…

Krok n

Od n-tego wiersza odejmuje się pierwszy pomnożony przez a_n1:

przy czym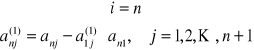

Etap redukcji k=2

Krok 1

Drugi wiersz dzielimy przez a₂₂:

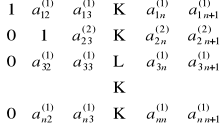
przy czym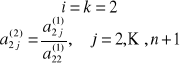

Krok 2

Od pierwszego wiersza odejmuje się drugi wiersz pomnożony przez
:

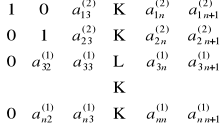
przy czym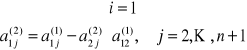

Krok 3

Od trzeciego wiersza odejmuje się drugi pomnożony przez
:

przy czym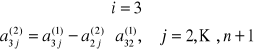

…

Krok n

Od n-tego wiersza odejmuje się drugi pomnożony przez
:

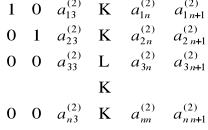
przy czym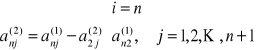

Etap redukcji k=n

Krok 1

N-ty wiersz dzielimy przez
:

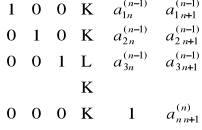
przy czym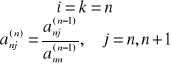

Krok 2

Od pierwszego wiersza odejmujemy n-ty pomnożony przez
:

przy czym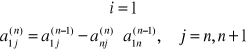

…

W kroku n-tym przekształca się n-1 równanie kończąc etap pełnej eliminacji. Stąd
, czyli:

,
,
, …,
.

Ogólnie uzyskuje się:

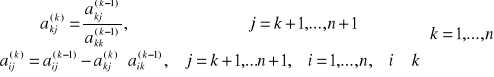
Ilość operacji:
, czyli dla n=10 wynosi 550.

Przykład: k=2

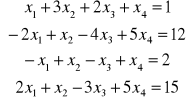
k=0 k=3

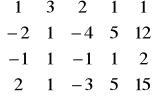
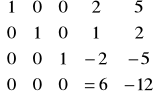
k=1 k=4

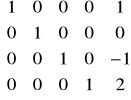
Rozwiązanie:

2. Algorytm metody Gaussa-Jordana

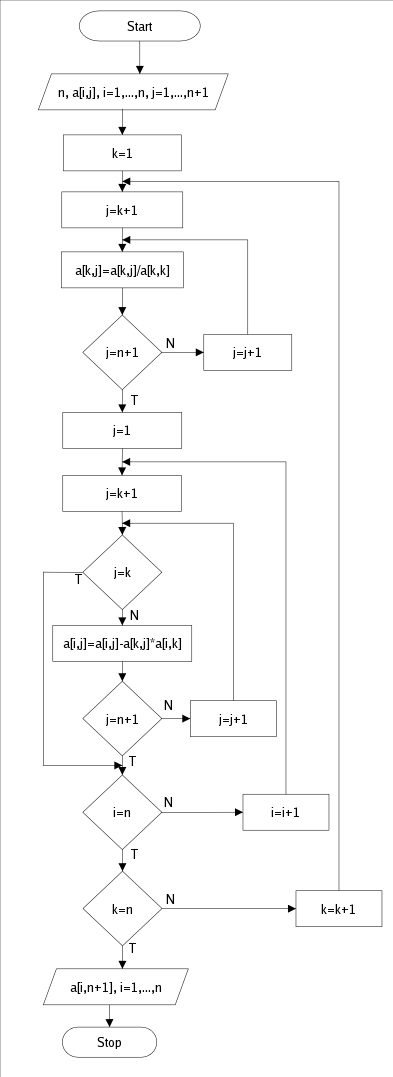
Główna przekątna - przekątna, na której leżą elementy dla których i=k, tj. a₁₁, a_22, a₃₃, ...

Strona 5 / 8

---