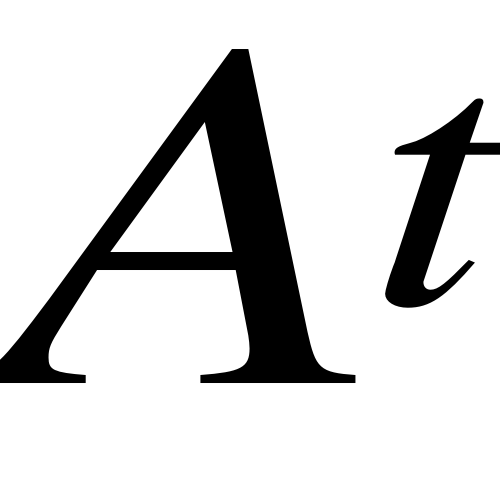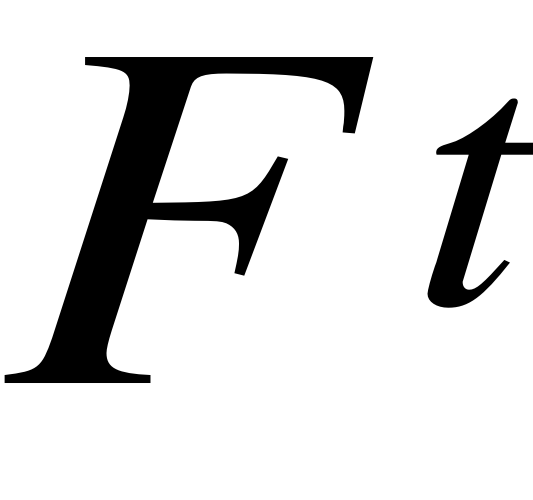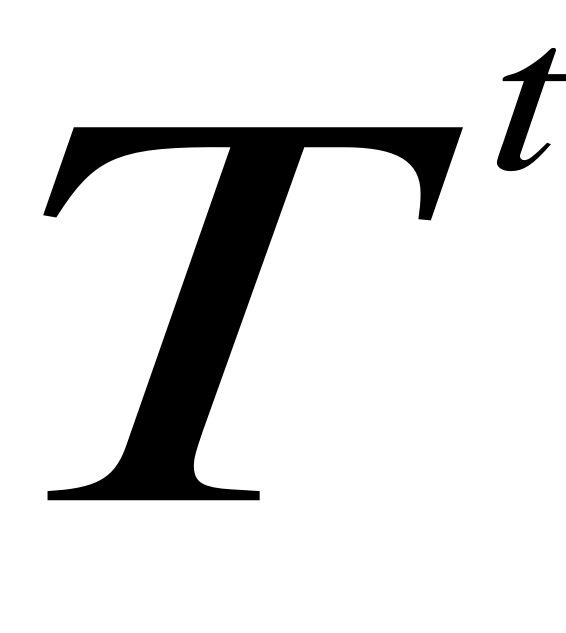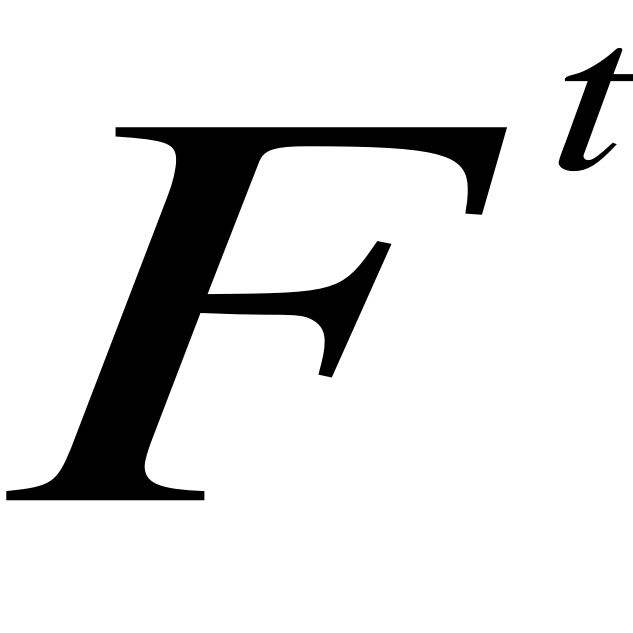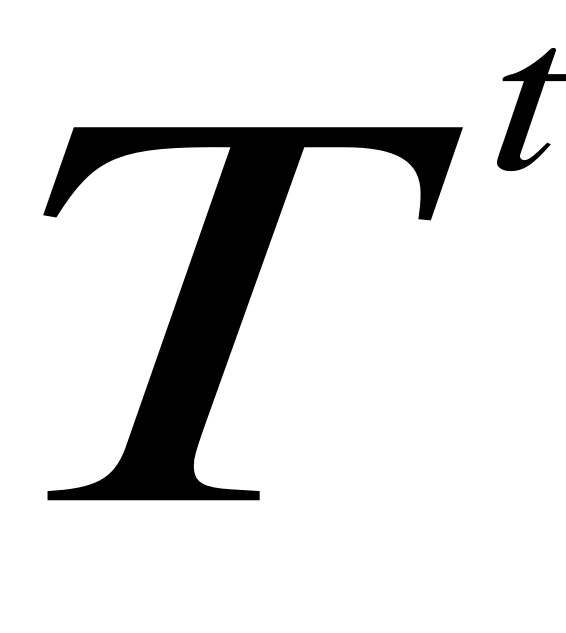Źródła:

http://www.econom.pl/download/nauka/prognozowanie.pdf

http://www.ae.poznan.pl/att/Doktoranckie_WZ/prognozowanie_II.doc

http://cne.gmu.edu/modules/dau/stat/dau2_frm.html

http://kbo.ae.poznan.pl/gaspars/laboratoria_pis/SzeregiCzasowe1.xls

http://cne.gmu.edu/modules/dau/stat/dau2_frm.html

J. Heizer, B. Render, Operations Management, 6th edition, Prentice Hall 2001

Nieekonometryczne metody prognozowania, oparte na szeregu czasowym

Szereg czasowy:

Prognoza na okres T+1 (np. miesiąc)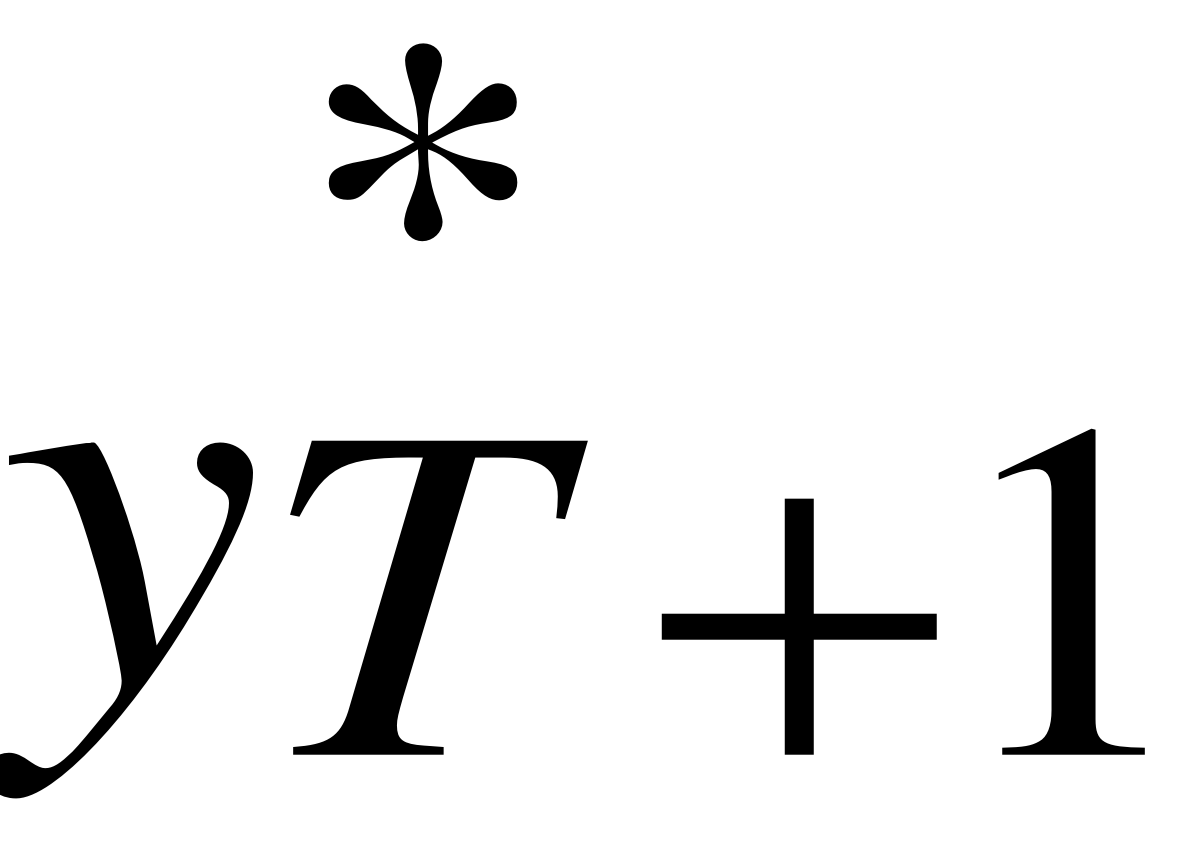

Metoda naiwna (Random Walk Model); prognozowana wielkość (np. popyt) w następnym okresie będzie taka sama jak w ostatnim (najbliższym aktualnemu)

1. Jeśli wahania przypadkowe wokół stałego poziomu, to
   

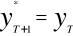
2. Jeśli wahania także sezonowe, to
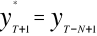
   (jednoimienne okresy)

3. Jeśli wahania przypadkowe oraz tendencja zmian w czasie, to są dwie możliwości:

- przyrost bezwzględny,

- przyrost względny,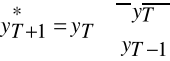

Metoda średniej arytmetycznej (Simple Mean Forecasting Model, long-term mean model)

A = średnia arytmetyczna =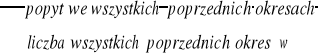

inny zapis: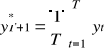

Metoda średniej ruchomej (Moving Average Model)

Wykorzystuje się średnią danych (obserwacji rzeczywistych wartości, np. popytu) z n ostatnich okresów do prognozowania następnego okresu:

MA(n) = średnia ruchoma =

n -liczba okresów branych pod uwagę w obliczeniach np. 4,5,6 mies.

Zaleta w porównaniu do metody średniej arytmetycznej: poprawa dokładności prognoz (mniejsza „przypadkowość”)

Wada (ogólna): wszystkie wartości historyczne mają takie same wagi

Metoda oparta na ważonej średniej ruchomej
(Weighted Moving Average Model)

WMA(n)= średnia ruchoma ważona (np. popytu) =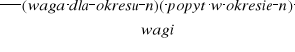

inny zapis: WMA(3) = F_t+1 = w₁(D_t) + w₂(D_t-1) + w₃(D_t-2) gdzie ∑w_i = 1, D_t-pomiary

często wykorzystywane wagi:

• wagi liniowe:

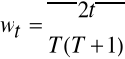
dla t = 1, 2, ..., T;

np. T=3 =>

• wagi harmoniczne:

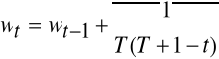
dla t = 1, 2, ..., T przy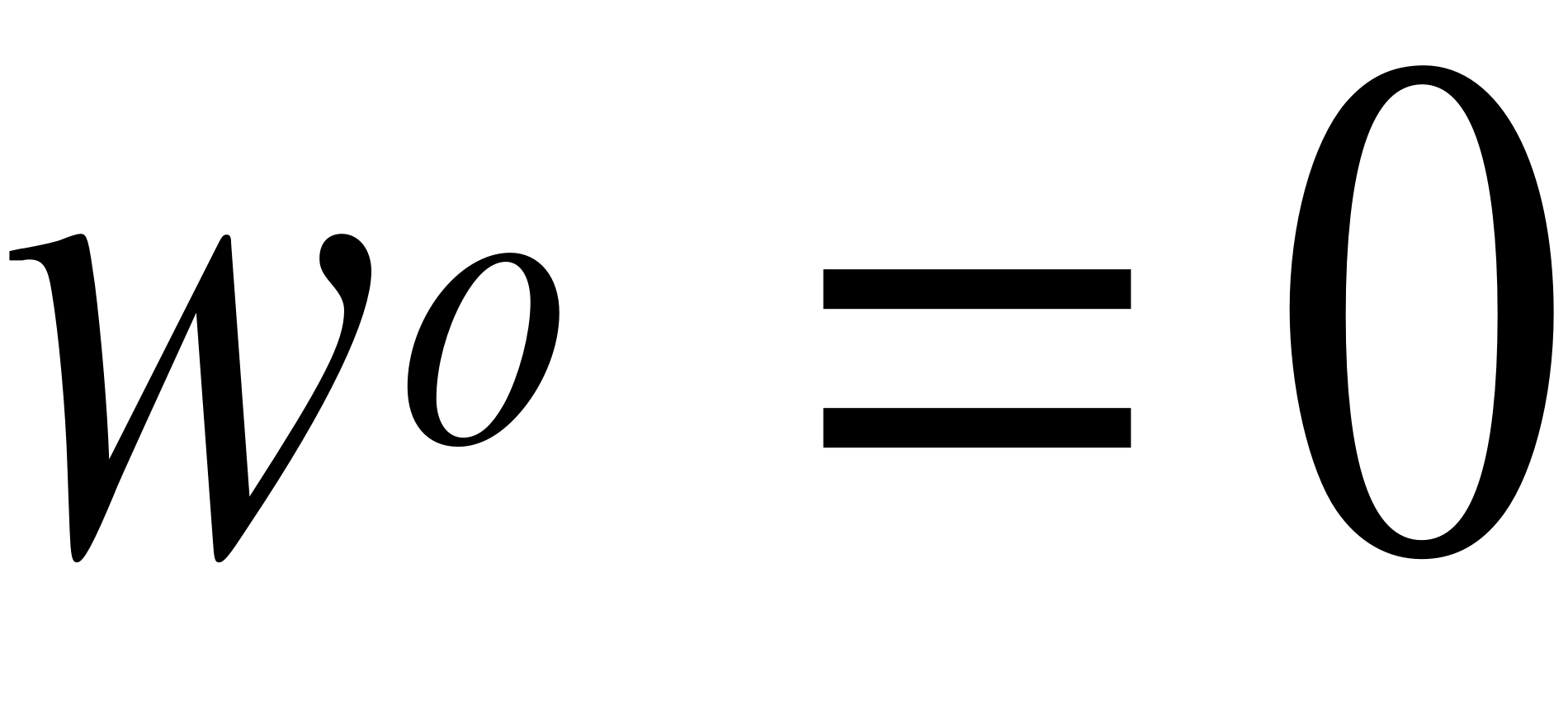
;

np. T = 3 =>

np. T = 2 =>

• wagi wykładnicze

Metoda oparta na wygładzaniu wykładniczym (exponential smoothing)

Jest to rozwinięcie techniki średniej ruchomej (ważonej) w której wagi wyliczane są zgodnie z funkcją wykładniczą. Powoduje wykładnicze „postarzanie” informacji.

Zaleta: potrzeba niewielkiej liczby danych z przeszłości.

Nowa prognoza = prognoza dla poprzedniego okresu + stała wygładzania (poprzednia obserwacja-prognoza dla poprzedniego okresu)

α - stała wygładzania (0 ≤ α ≤ 1)

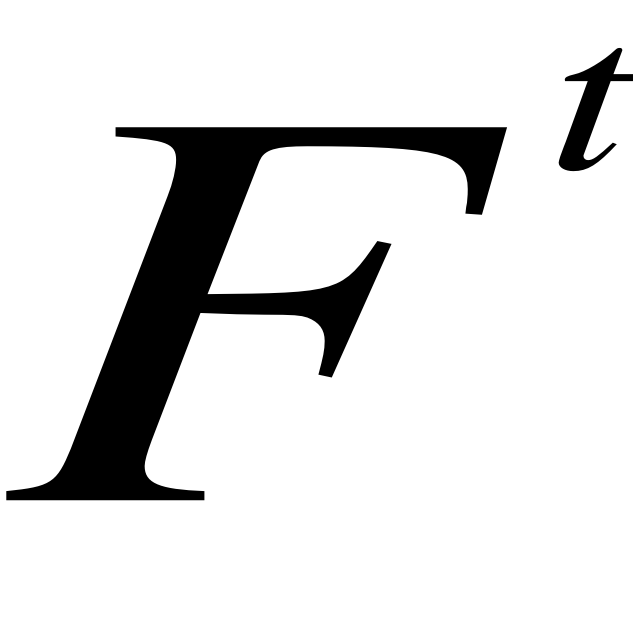
- nowa prognoza;

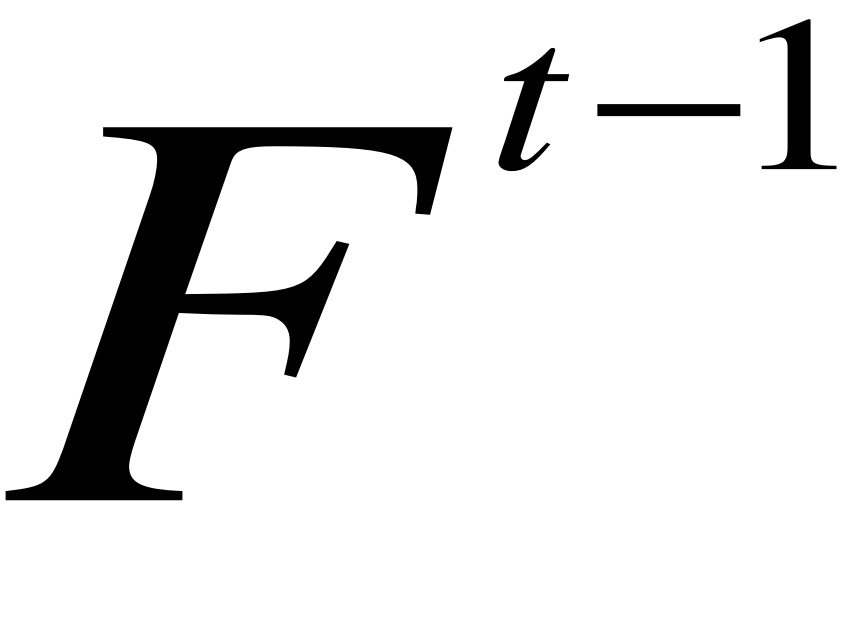
- poprzednia prognoza;

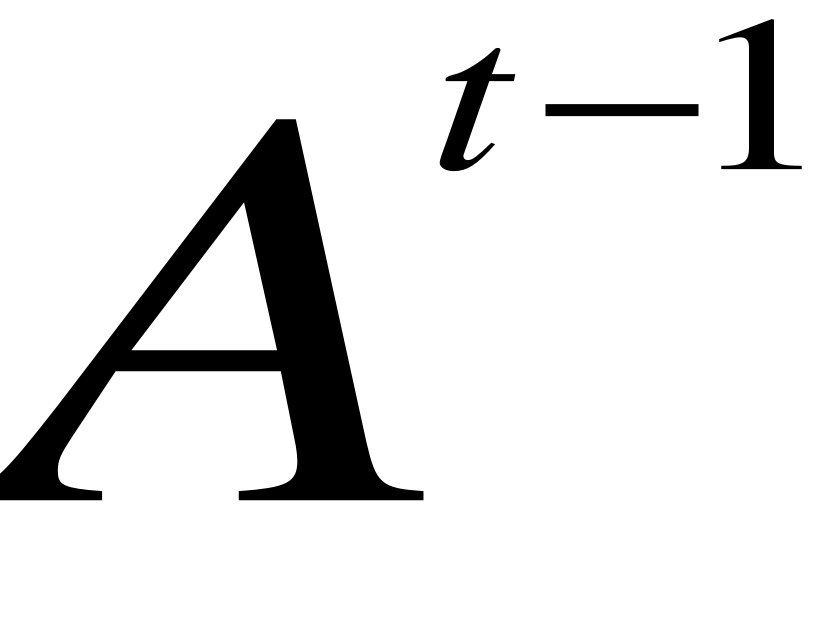
- rzeczywista wartość w poprzednim okresie

α przeważnie znajduje się między 0,05 a 0,5

α wysokie => silniej uwzględnia ostatnie dane; α niskie => silniej uwzględnia dawniejsze dane

gdy α =1 =>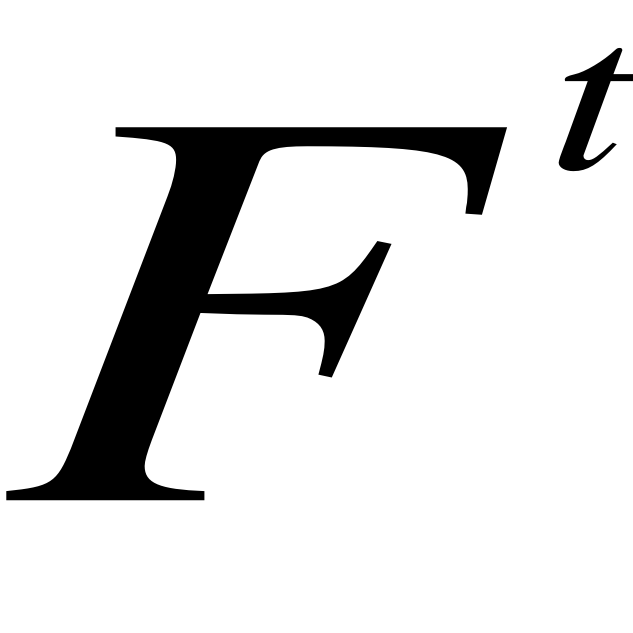
=
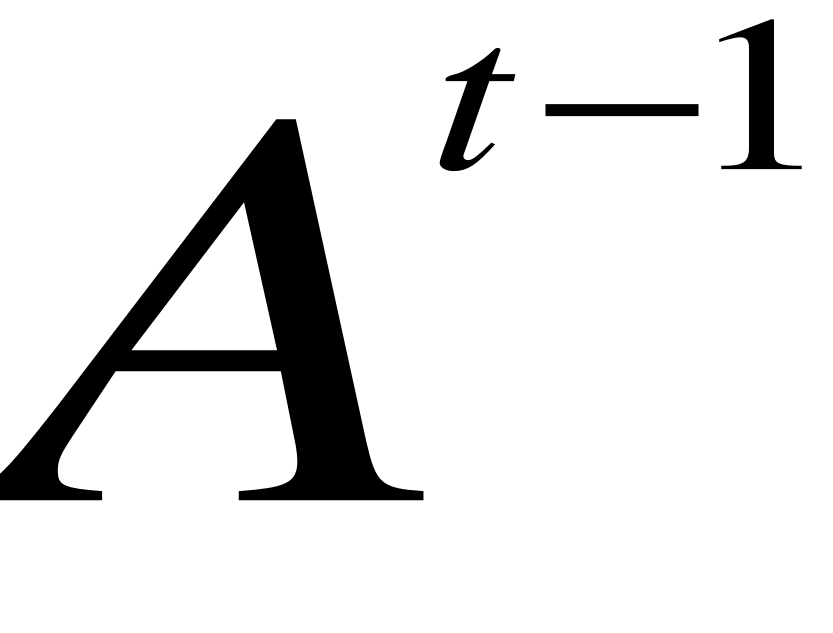
(prognozowanie naiwne); gdy α rośnie => spada istotność starszych okresów

Metoda wykładniczo ważonej średniej ruchomej
(Exponential Weighted Moving Average Model)

Jest rozwinięciem metody wyrównywania wykładniczego.

Uwaga: zamiast ostatniej obserwacji można wstawić średnią ruchomą z ostatnich n miesięcy!

Metoda wykładzania wykładniczego z uwzględnieniem trendu (Exponenential Smoothing with Trend Adjustment), metoda Holta

Prognoza uwzględniająca trend (FIT_t) = (F_t) + (T_t)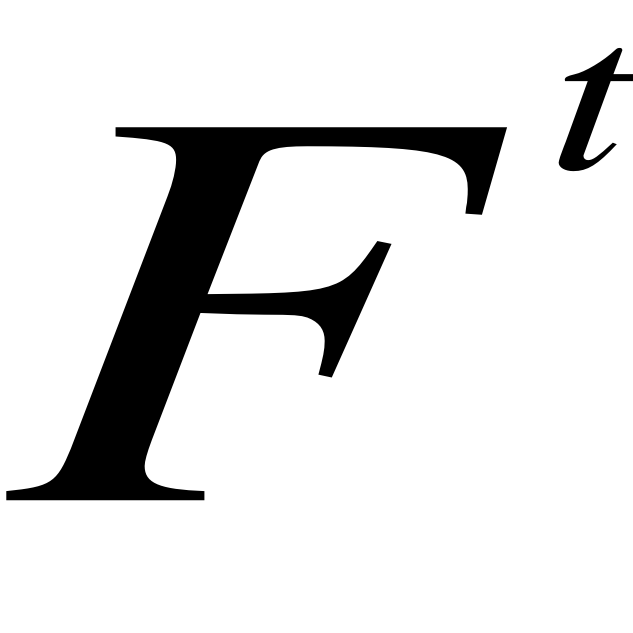

= α (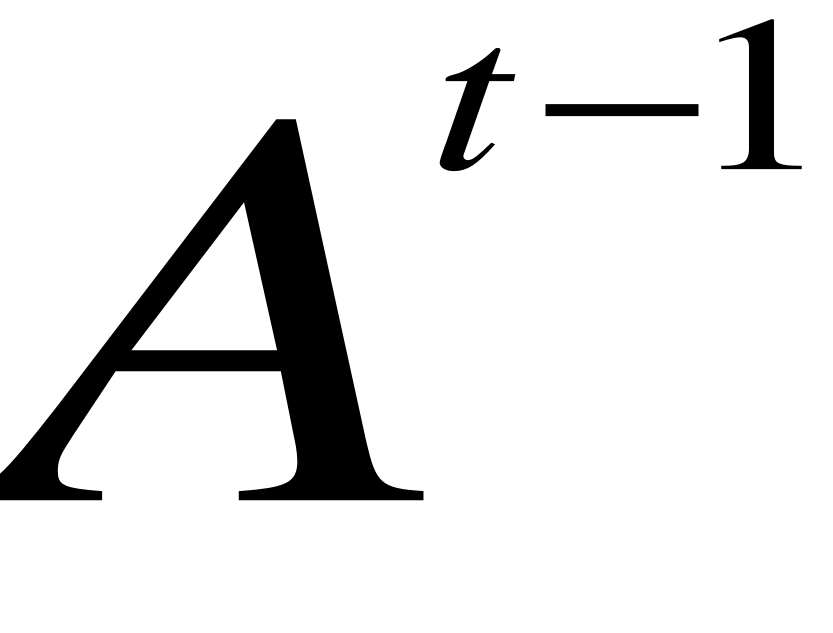
) + (1- α) (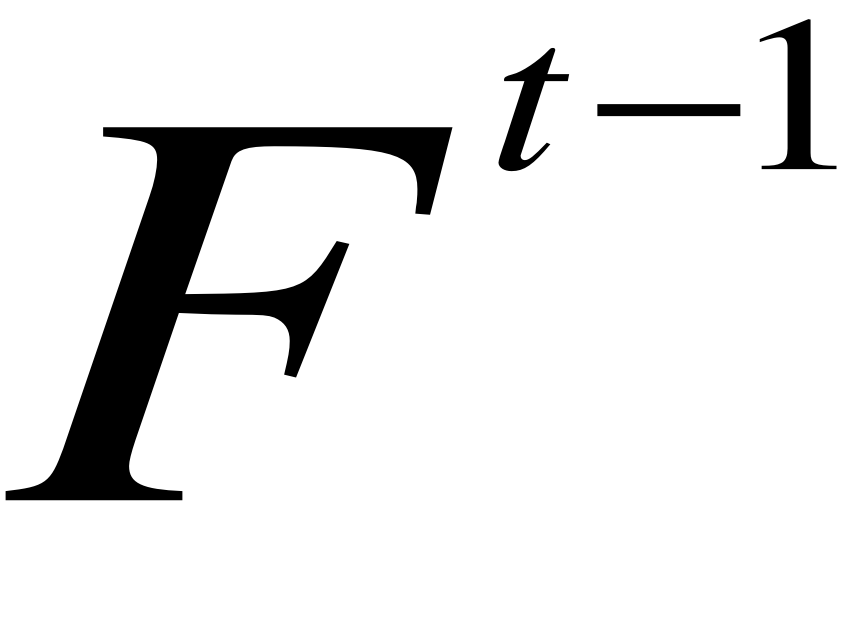
+
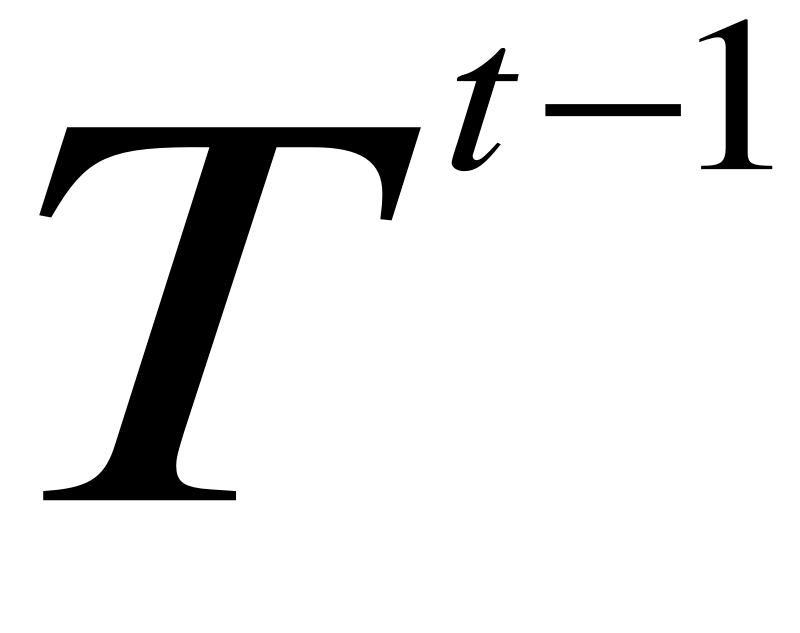
), wygładza część stałą szeregu czasowego

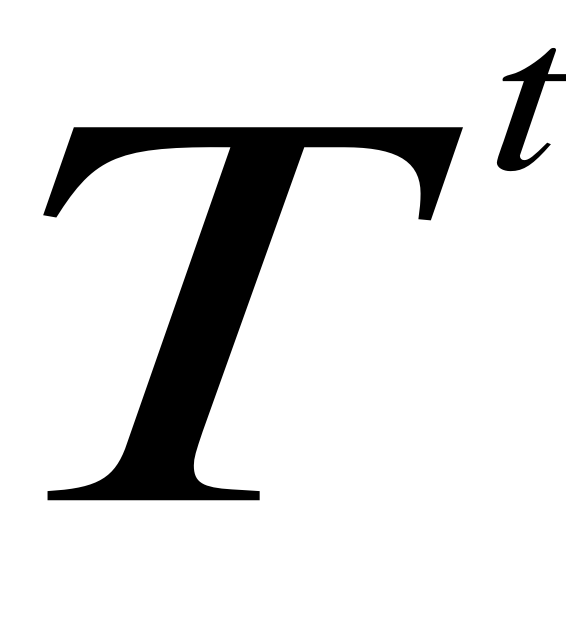
= β (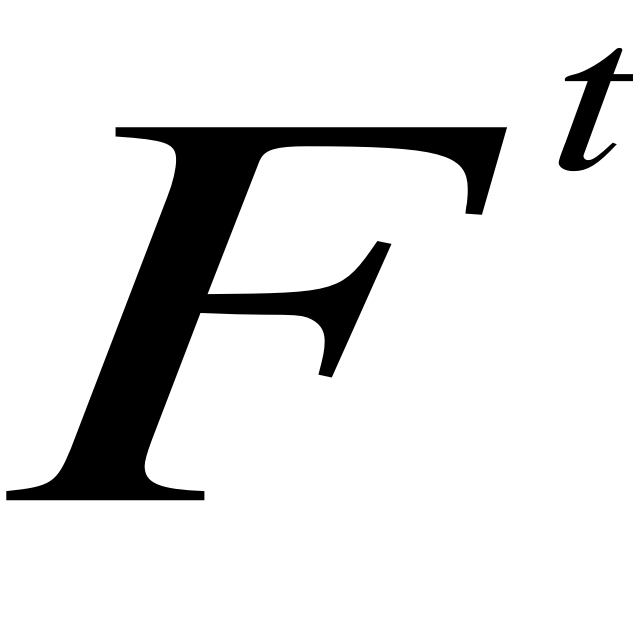
-
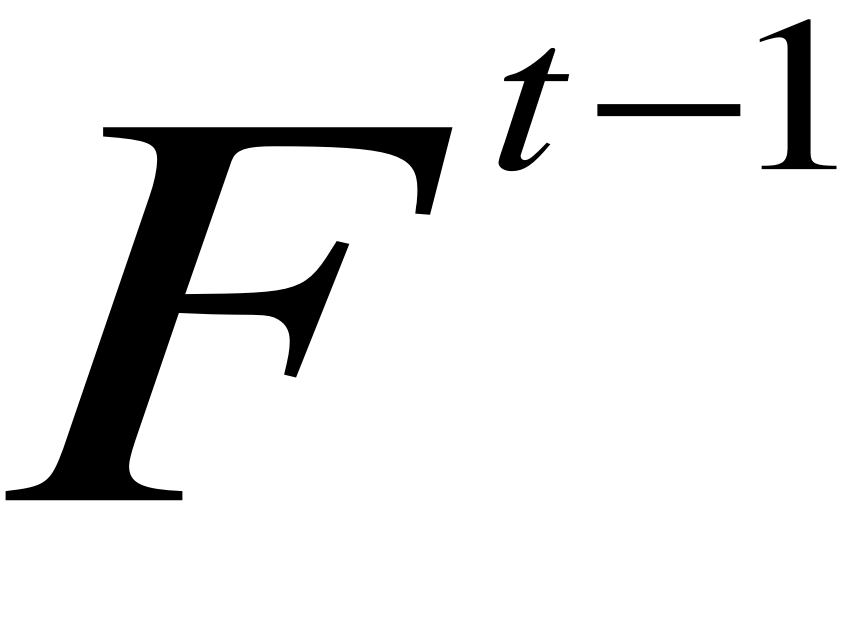
) + (1-β)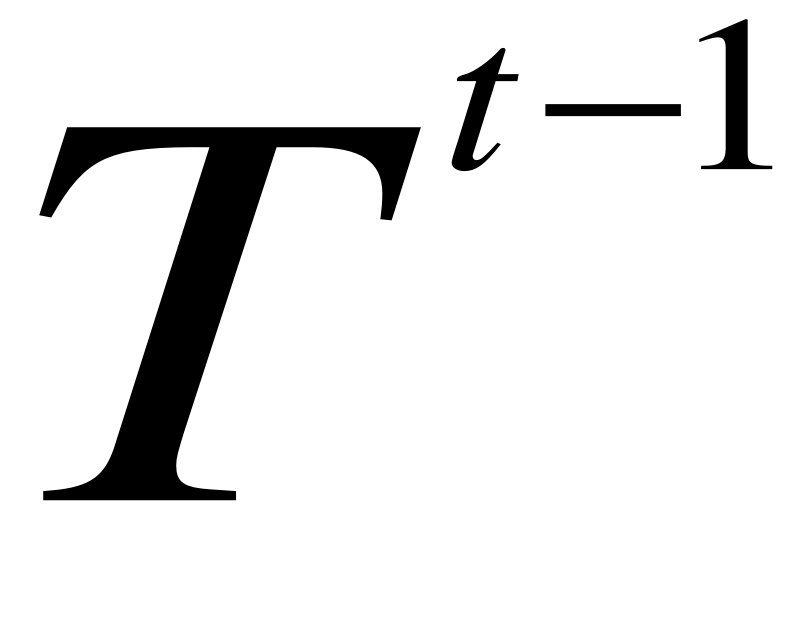
, wygładza przyrost szeregu czasowego w jednostce czasu

stała wygładzania dla średniej (0 ≤ α ≤1)

stała wygładzania dla trendu (0 ≤ β ≤1)

Trzy kroki obliczeń:

Krok 1: obliczyć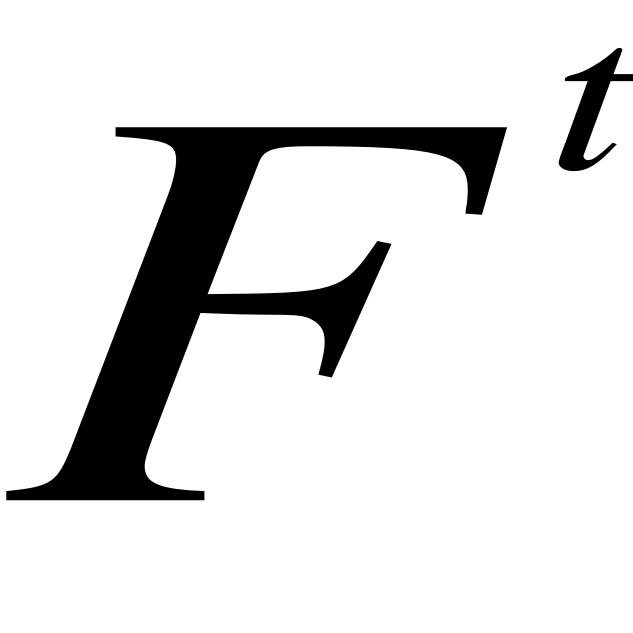
czyli wykładniczo wygładzoną prognozę dla okresu t

Krok 2: obliczyć wykładniczo wygładzony trend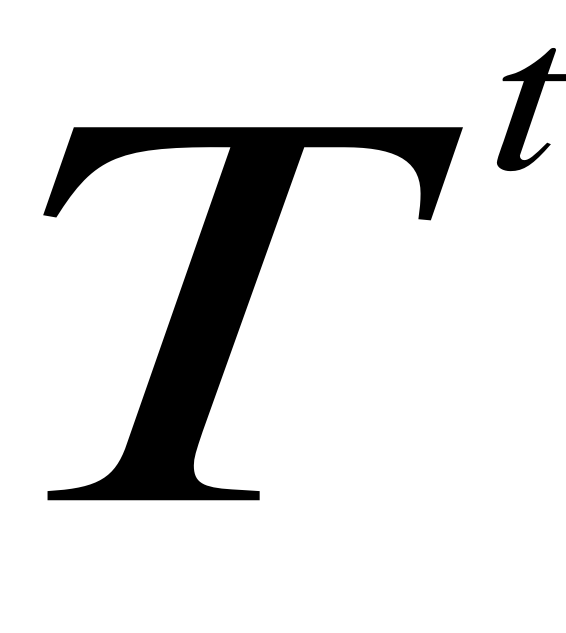

Krok 3. obliczyć skorygowaną prognozę FIT_t

Uwaga1: niska β -> mniejsza istotność aktualnego trendu (wygładza aktualny trend)

Uwaga2: jak dobierać współczynnik β ? Odpowiedź: MAD, prób i błędówBłąd prognozy (np. popytu) = popyt (rzeczywisty) - prognoza

średnie bezwzględne odchylenie,
średni bezwzględny błąd prognozy ex post
(Mean Absolute Deviation)
MAD = =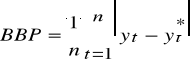

średni błąd kwadratowyex post
(Mean Square Error)
MSE = =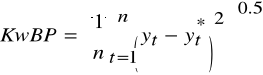

współczynnik Teila, współczynnik rozbieżności
(inequality coefficient);

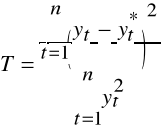
Średni względny błąd prognozy ex post

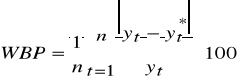
Zadanie 1. Sklep sprzedaje przyczepy kempingowe. Proszę opracować prognozę sprzedaży metodami: naiwną, średniej arytmetycznej, średniej ruchomej trzymiesięcznej, ważonej średniej miesięcznej (trzymiesięcznej) o wagach : 1, 2, 3; wagach liniowych, wagach harmonicznych. Proszę narysować wykres i wyznaczyć błędy prognozy.

Miesiąc	Sprzedaż rzeczywista[sztuk]	Prognozy …
Styczeń	10
Luty	12
Marzec	13
Kwiecień	16
Maj	19
Czerwiec	23
Lipiec	26
Sierpień	30
Wrzesień	28
Październik	18
Listopad	16
Grudzień	14

Zadanie 2. W pewnym porcie obserwowano w ostatnich 2 latach duże opóźnienia w rozładowywaniu ziarna ze statków. Naczelnik pragnie sprawdzić czy metoda wygładzania wykładniczego nadaje się do przewidywania ilości nierozładowanego ładunku. W pierwszym kwartale przewidywano nierozładowanie 175 ton.

Proszę opracować prognozę dla α = 0.1 oraz α = 0.5, obliczyć bezwzględne wartości błędów oraz błędy MAD i MSE.

Kwartał	Nierozładowany ładunek [tony]	Prognoza [tony]
1	180	175
2	168
3	159
4	175
5	190
6	205
7	180
8	182
9	???

Zadanie 3. W pewnej fabryce prognoza kwartalnego zapotrzebowania na części zamienne filtrów zanieczyszczeń wyznaczana jest za pomocą metody wygładzania z uwzględnieniem trendu addytywnego. Niech współczynnik α = 0.2 oraz β = 0.4, pierwsza prognoza (wygładzająca część stałą szeregu czasowego F₁ = 11, pierwsza prognoza trendu T₁ = 2. Proszę wyznaczyć prognozę całkowitą, obliczyć bezwzględne wartości błędów oraz błędy MAD i MSE.

Kwartał	zapotrzebowanie [sztuki]	prognoza cząstkowa [sztuki]	wygładzony trend [sztuki]	FITt prognoza całkowita [sztuki]
1	12	11	2	-
2	19
3	22
4	19
5	25
6	23
7	30
8	29
9	35
10	??

Przykład: α =0.2, β =0.4, F₁=11, T₁=2

miesiąc				FITt
1	12	11,00	2,00	-
2	19	12,80	1,92	14,72
3	22	15,58	2,26	17,84
4	19	18,67	2,60	21,27
5	25	20,81	2,41	23,23
6	23	23,58	2,56	26,14
7	30	25,51	2,30	27,81
8	29	28,25	2,48	30,73
9	35	30,39	2,34	32,73
10	-	33,18	2,52	14,72

Krok 1: F₂ = αA₁ + (1 - α)(F₁ + T₁) = 0,2 * 12 + (1 - 0,2) * (11 + 2) = 12,8

Krok 2: T₂ = β (F₂ - F₁) + (1 - β) T₁ = 0,4 * (12,8 - 11) + (1 - 0,4) * 2 = 1,92

Krok 3: FIT₂ = F₂+ T₂ = 12,8 + 1,92 = 14,72

Krok 1: F₃ = αA₂ + (1 - α)(F₂ + T₂) = 0,2 * 19 + (1 - 0,2) * (12,8 + 1,92) = 15,58

Krok 2: T₃ = β (F₃ - F₂) + (1 - β) T₂ = 0,4 * (15,58 - 12,8) + (1 - 0,4) * 1,92 = 2,26

Krok 3: FIT₃ = F₃+ T₃ = 15,58 + 2,26 = 17,84

8

3

---