ZADANIA Z TECHNOLOGII CHEMICZNEJ

Przykład 1

Chlorek metylu otrzymuje się w procesie chlorowania metanu gazowym chlorem (strumień W_B). Strumień W_A oprócz metanu zawiera azot (2 % molowe).

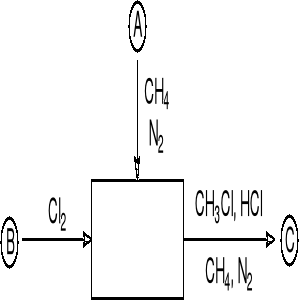
Proces chlorowania metanu prowadzi się stosując nadmiar metanu w stosunku do chloru. W reakcji:

CH₄ + Cl₂ = CH₃Cl + HCl

chlor zużywa się całkowicie.

Wydajność przetwarzania metanu w chlorek metylu wynosi

0≤ η≤1

Oblicz zależność ułamka molowego CH₃Cl w strumieniu W_C od wydajności procesu η.

aCH3Cl = f(η)

Rozwiązanie

Za podstawę bilansu przyjęto natężenie strumienia zawierającego metan i 2 % molowe azotu: W_A = 100 kmol/h.

Na podstawie przyjętej podstawie bilansu obliczamy natężenie strumienia metanu w gazie zasilającym reaktor W_A[CH₄]. Wynosi on 98 kmol/h. Azot stanowi resztę strumienia tj. 2 kmol/h.

Z definicji ၨ obliczamy zawartość CH₃Cl w strumieniu C: W_C[CH₃Cl] = W_A[CH₄] Ⴗ ၨ

czyli

W_C[CH₃Cl] = 98 ၨ

Z bilansu węgla (C) obliczamy zawartość metanu w strumieniu C:

W_A[CH₄] = W_C[CH₄] + W_C[CH₃Cl]

W_C[CH₄] = 98 - 98 ၨ = 98(1-ၨ)

Z bilansu wodoru obliczamy natężenie strumienia HCl w gazach po reakcji.

4 W_A[CH₄] = 4 W_C[CH₄] + 3W_C[CH₃Cl] + W_C[HCl]

W_C[HCl] = 4 W_A[CH₄] - 4 W_C[CH₄] - 3W_C[CH₃Cl]

W_C[HCl] = 98ၨ

Zawartość chloru w strumieniu A obliczamy na podstawie bilansu chloru:

2W_A[Cl₂] = W_C[CH₃Cl] + W_C[HCl]

W_A[Cl₂] = 98ၨ

Ponieważ azot nie bierze udziału w reakcji natężenie strumienia W_A[N₂] jest identyczne jak w strumieniu C:

W_A[N₂] = W_C[N₂]

Bilans reaktora przedstawiono w tabeli 1.

Tabela 1. Bilans masy

Przychód, kmol/h	Rozchód, kmol/h
CH4 98	CH4 98 (1 - )
N2 2	N2 2
Cl2 98	CH3Cl 98
	HCl 98
	100 + 98 = WC

Ułamek molowy chlorku metylu w strumieniu C obliczamy ze wzoru:

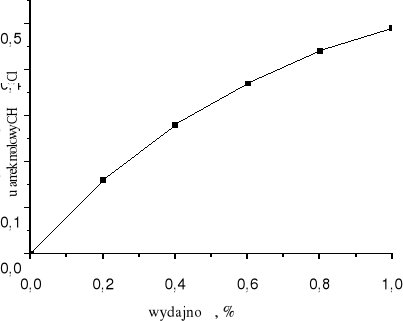
Wartość η może zmieniać się od 0 do 1. Jeżeli η = 0, ułamek molowy chlorku metylu w strumieniu C wynosi 0. Ze wzrostem wydajności rośnie ułamek molowy chlorku metylu w strumieniu C. Dla maksymalnej wydajności (η = 1) wynosi on 0,495.

Przykład 2

Utlenianie SO₂ prowadzi się na katalizatorach wanadowych. Do reaktora doprowadza się gazy uzyskane ze spalania siarki o składzie (w procentach molowych) 10 %, SO₂, 11 % O₂ i 79 % N₂. Stopień przemiany SO₂ w SO₃ uzyskiwany na katalizatorze oznacza się x i definiuje

x =

Zawartość SO₂ w gazach poreakcyjnych wynosi a (% mol.). Schemat instalacji:

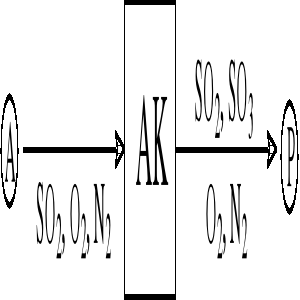
Przyjmując za podstawę bilansu natężenie strumienia A: W_A = 100 kmol/h wyznacz i przedstaw graficznie zależność a = f(x)

Rozwiązanie

Za podstawę bilansu przyjęto natężenie strumienia A (W_A = 100 kmol/h) zawierającego 10 % SO₂, 11 % O₂ i 79 % N₂ (% molowe).

Na podstawie przyjętej podstawy bilansu zawartość SO₂, O₂ i N₂ w strumieniu A wynosi odpowiednio 10, 11 i 79 kmol/h.

Z definicji stopnia przemiany SO₂ do SO₃ obliczono zawartość SO₃ w strumieniu P: W_P[SO₃] = W_A[SO₂] Ⴗ x

czyli:

W_P[SO₃] = 10 x

Z bilansu siarki (S) obliczamy zawartość SO₂ w strumieniu P:

W_A[SO₂] = W_P[SO₃] + W_P[SO₂]

W_P[SO₂] = 10 - 10x = 10(1-x)

Zawartość tlenu w strumieniu P (W_P[SO₂]) obliczamy z bilansu tlenu:

2W_A[SO₂] + 2W_A[O₂] = 3W_P[SO₃] + 2W_P[SO₂] + 2W_P[O₂]

Ponieważ azot nie bierze udziału w reakcji natężenie strumienia W_A[N₂] jest identyczne jak w strumieniu P:

W_A[N₂] = W_P[N₂]

Bilans reaktora przedstawiono w tabeli 2.

Tabela 2. Bilans masy

Przychód, kmol/h	Rozchód, kmol/h
SO2 10	SO2 10(1-x)
N2 79	N2 79
O2 11	SO3 10x
	O2 11- 5x
	100 - 5x = WP

Procent molowy SO₂ w strumieniu P wynosi:

, %

, %

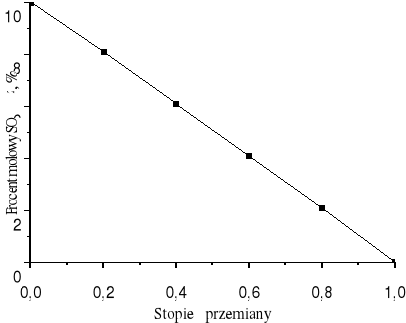
Wartość stopnia przemiany dwutlenku siarki (IV) do dwutlenku siarki (VI) może zmieniać się od 0 do 1. Jeżeli stopień przemiany wynosi 0 procent molowy SO₂ w strumieniu P wynosi 10 czyli tyle ile w strumieniu A. Ze wzrostem x maleje zawartość SO₂ w strumieniu P. Dla x = 1 w strumieniu P występuje wyłącznie SO₃, azot i nieprzereagowany tlen.

Przykład 3

Synteza amoniaku z wodoru i azotu

3H₂ + N₂ = 2NH₃

jest reakcją odwracalną i egzotermiczną, której stała równowagi maleje ze wzrostem temperatury. Ze wzrostem temperatury maleją więc także równowagowe stopnie przemiany wodoru i azotu. W celu uzyskania odpowiednich szybkości reakcji syntezy NH₃ stosuje się katalizator żelazowy, który jest aktywny w zakresie temperatury 400-500 ⁰C. W tym zakresie temperatury wartość stałej równowagi jest mała. W celu zwiększenia równowagowego stopnia przemiany w praktyce przemysłowej stosuje się ciśnienie 10-30MPa. W tych warunkach zawartość amoniaku w gazie opuszczającym reaktor nie przekracza 20 % mol.

Gaz do syntezy amoniaku zawiera, oprócz głównych składników tj. azotu i wodoru, również niewielkie ilości (ok. 2%) gazów obojętnych głównie metanu i argonu (argon pochodzi z powietrza). W celu maksymalnego wykorzystania substratów proces syntezy amoniaku prowadzi się w układzie zamkniętym z recyrkulacją gazu po wydzieleniu z niego otrzymanego amoniaku.

Syntezę amoniaku prowadzi się w reaktorze, do którego doprowadza się wodór i azot z domieszką argonu. Ułamek molowy argonu w strumieniu A wynosi 0,02. Stosunek molowy wodoru do azotu w strumieniu A wynosi 2,7. Przyjmując, że do instalacji doprowadza się 100 kmol/h gazu (W_A = 100 kmol/h) oblicz zależność ułamka molowego amoniaku w strumieniu B od stopnia przemiany wodoru w reaktorze (a_NH3 = f(x)), 0 Ⴃ x Ⴃ 0,2).

Rozwiązanie

Na podstawie przyjętej podstawy bilansu natężenie strumienia argonu (W_A[Ar]) wynosi 2 kmol/h.

Natężenie strumienia wodoru i azotu w strumieniu A wynosi 98 kmol/h. Stosunek natężenia strumienia wodoru do azotu wynosi 2,7.

W_A[H₂] + W_A[N₂] = 98

W_A[H₂] /W_A[N₂] = 2,7

czyli:

W_A[H₂] = 71,5 kmol/h i W_A[N₂] = 26,5 kmol/h

Wykorzystując definicję stopnia przemiany wodoru w reaktorze obliczamy natężenie strumienia wodoru w gazie po reakcji:

W_B[H₂] = W_A[H₂](1-x) = 71,5(1-x)

Natężenie strumienia wyprodukowanego amoniaku obliczamy z bilansu wodoru w obszarze reaktora:

2W_A[H₂] = 2W_B[H₂] + 3W_B[NH₃]

a stąd

W_B[NH₃] = 47,7x

Natężenie strumienia nieprzereagowanego azotu (W_B[N₂]) obliczamy na podstawie bilansu azotu:

2W_A[N₂] = 2W_B[N₂] + W_B[NH₃]

z czego wynika:

W_B[N₂] = 26,5 - 23,9x

Ponieważ argon nie bierze udziału w reakcji natężenie strumienia W_A[Ar] jest identyczne jak w strumieniu B:

W_B[Ar] = W_B[Ar]

W_B[Ar] = 2

Bilans reaktora przedstawiono w tabeli 3.

Tabela 3. Bilans masy

Przychód, kmol/h	Rozchód, kmol/h
H2 71,5	H2 71,5(1-x)
N2 26,5	N2 26,5-23,9x
Ar 2	Ar 2
	NH3 47,7x
	100 - 47,7x = WB

Zależność ułamka molowego amoniaku w strumieniu B od stopnia przemiany wodoru obliczamy ze wzoru:

z którego wynika:

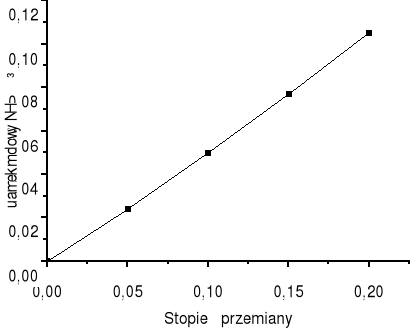
Dla wartości stopnia przemiany wodoru równego 0 w reaktorze nie zachodzi reakcja i skład strumienia B jest taki jak strumienia A. Wraz ze wzrostem wartości stopnia przemiany wodoru zawartość amoniaku w strumieniu B wzrasta. Dla x = 0,2 ułamek molowy amoniaku w gazie po reakcji wynosi 0,105.

Przykład 4

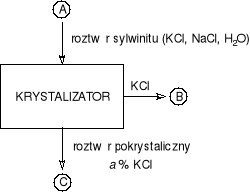
Chlorek potasu otrzymuje się z wodnego roztworu sylwinitu (sól, w której potas występuje w postaci minerału - sylwinu) zawierającego 35 % mas. KCl. W procesie krystalizacji otrzymuje się czysty KCl oraz roztwór pokrystalizacyjny zawierający a % mas. KCl. Oblicz zależność wydajności krystalizacji od stężenia KCl w roztworze pokrystalizacyjnym.

ၨ = f(a)

ၨ =

Obliczenia prowadź zakładając, że w ciągu 1 godziny przerabia się 1000 kg roztworu sylwinitu
(G_A = 1000 kg/h).

Rozwiązanie

Natężenie strumienia KCl w roztworze sylwinitu (G_A[KCl]) wynosi:

G_A[KCl] = 0,35G_A

czyli:

G_A[KCl] = 350 kg/h

Natężenie strumieniu wody i NaCl w roztworze sylwinitu wynosi 650 kg/h.

Natężenie strumienia otrzymywanego KCl (G_B[KCl]) obliczamy z wydajności procesu (ၨ = G_B[KCl]/G_A[KCl]).

Podstawiając otrzymujemy:

G_B[KCl] = 350ၨ

Natężenie strumienia KCl w roztworze pokrystalizacyjny obliczamy z bilansu KCl w obszarze krystalizatora:

G_A[KCl] = G_B[KCl] + G_C[KCl]

z czego wynika:

G_C[KCl] = 350(1-ၨ)

W roztworze pokrystalizacyjnym natężenie strumienia wody i NaCl wynosi 650 kg/h.

Bilans reaktora przedstawiono w tabeli 4.

Tabela 4. Bilans masy

Przychód, kg/h	Rozchód, kg/h
KCl 350	B: KCl 350ၨ
NaCl +H2O 650	C: KCl 350(1-ၨ)
	NaCl +H2O 650

Procent masowy KCl w strumieniu C wynosi:

, %

stąd wynika:

, %

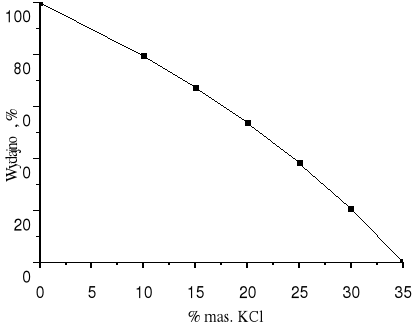
Wydajność krystalizacji może zmieniać się od 0 do 100 %. 35 % KCl w strumieniu C oznacza, że wydajność procesu wynosi 0 (KCl nie wykrystalizował). W tym przypadku skład strumienia C jest taki sam jak strumienia A. Wartość ၨ wzrasta do 100 % gdy w strumieniu C nie występuje KCl.

Przykład 5

Prażąc piryt FeS₂ w strumieniu powietrza otrzymuje się gaz zawierający SO₂, O₂ i N₂ oraz wypałki - Fe₂O₃. Przyjmując, że ułamek molowy tlenu w strumieniu P wynosi
(
= W_P[O₂]/W_P) i ułamek molowy SO₂ w strumieniu P wynosi
(
= W_P[SO₂]/W_P), oblicz zależność
= f(
). Obliczenia przeprowadź przyjmując za podstawę bilansu 10 kmol/h gazu opuszczającego reaktor (W_P = 10 kmol/h).

Uproszczony skład powietrza: 20 % tlenu i 80 % azotu.

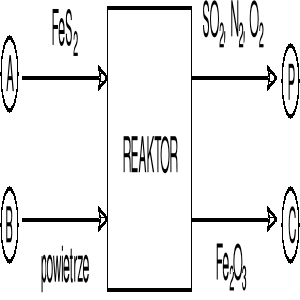
Rozwiązanie

Na podstawie przyjętej podstawy bilansu zawartość dwutlenku siarki (IV) w strumieniu P wynosi 10
kmol/h. Zawartości tlenu i azotu w strumieniu P wynoszą odpowiednio:
10
i 10
.

Z bilansu siarki w obszarze reaktora obliczamy natężenie strumienia pirytu FeS₂ :

2W_A[FeS₂] =W_P[SO₂]

W_A[FeS₂] = 0,5W_P[SO₂]

Z bilansu żelaza w obszarze reaktora obliczamy natężenie strumienia Fe₂O₃ :

W_A[FeS₂] =2W_CFe₂O₃]

W_C[Fe₂O₃] = 0,5W_A[FeS₂] = 2,5

Zawartość tlenu w strumieniu B (W_B[O₂]) obliczamy z bilansu tlenu:

2W_B[O₂] = 2W_P[SO₂] + 2W_P[O₂] +3W_C[Fe₂O₃]

stąd

W_B[O₂] = 13,75
+ 10

Ponieważ azot nie bierze udziału w reakcji natężenie strumienia W_B[N₂] jest identyczne jak w strumieniu P:

W_B[N₂] = W_P[N₂]

W_B[N₂] = 10(1-
-
)

Bilans reaktora przedstawiono w tabeli 5.

Tabela 5. Bilans masy

Przychód, kmol/h	Rozchód, kmol/h
FeS2 5	SO2 10
N2 10(1- - )	N2 10(1- - )
O2 13,75 + 10	O2 10
	Fe2O3 2,5

Zależność ułamka molowego dwutlenku siarki od ułamka molowego tlenu w strumieniu P obliczamy z zależności:

= 4

czyli:

= 0,154 - 0,77a_O2

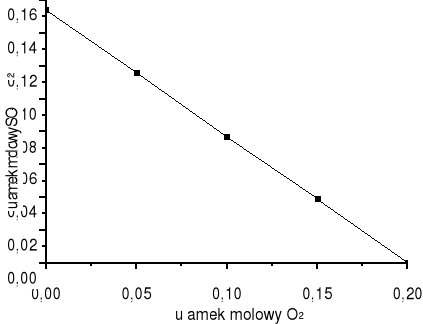
Wartość ułamka molowego SO₂ w strumieniu P może zmieniać się od 0 do 0,154. Gdy

= 0 oznacza to, że reakcja nie zachodzi i skład strumienia P jest taki jak strumienia B (powietrze). Dla
= 0 wartość ułamka molowego SO₂ wynosi 0,154. Oznacza to, że do reaktora wprowadzono stechiometryczną ilość FeS₂ i tlenu. W praktyce stosuje się nadmiar tlenu.

Przykład 6

Gaz zawierający CO, CO₂, H₂ i N₂ poddaje się konwersji parą wodną w celu wzbogacenia go w wodór. Reakcja konwersji zachodzi w/g równania

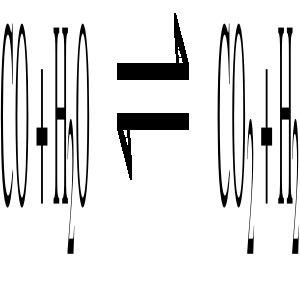
W procesie stosuje się nadmiar pary wodnej. Z gazów po konwersji usuwa się nieprzereagowaną parę wodną (strumień C). Uproszczony schemat instalacji przedstawia rysunek.

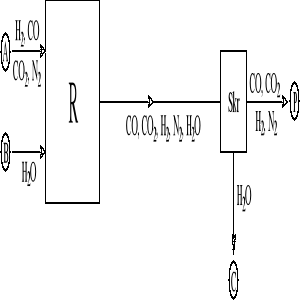
Przyjmując skład strumienia A: H₂ — 34 %, CO — 37 %, CO₂ — 4 %, N₂ — 25% molowych i stosunek natężenia strumienia pary wodnej (strumień B) do strumienia A: W_B/W_A = 1,5 oraz stopień przemiany (konwersji) tlenku węgla (II) w reaktorze 90 % oblicz ułamki molowe wodoru, tlenku węgla (II) i tlenku węgla (IV) w strumieniu P. Za podstawę bilansu należy przyjąć natężenie strumienia A: W_A = 100 kmol/h.

Rozwiązanie

Na podstawie przyjętej podstawy bilansu natężenie strumienia wodoru, tlenku węgla (II), tlenku węgla (IV) i azotu w gazie wprowadzanym do reaktora wynosi odpowiednio:

W_A[H₂] = 34 kmol/h

W_A[CO] = 37 kmol/h

W_A[CO₂] = 4 kmol/h

W_A[N₂] = 25 kmol/h

Z zależności:

= 1,5

obliczamy natężenie strumienia W_B

W_B[H₂O] = 150 kmol/h

Z definicji stopnia przemiany CO:

x =

możemy obliczyć W_D[CO]

W_D[CO] = W_A[CO](1-x) = 37 Ⴗ 0,1 = 3,7 kmol/h

W_P[CO] jest równe natężeniu strumienia CO w strumieniu D (W_D[CO]).

W_P[CO] = W_D[CO]

W_P[CO] = 3,7 kmol/h

Natężenie strumienia CO₂ w gazie po konwersji obliczamy z bilansu węgla.

W_A[CO] + W_A[CO₂] = W_P[CO] + W_P[CO₂]

stąd

W_P[CO₂] = 37,3 kmol/h

Natężenie strumienia nieprzereagowanej pary wodnej obliczamy z bilansu tlenu.

W_A[CO] + 2W_A[CO₂] + W_B[H₂O] = W_P[CO] + 2W_P[CO₂] + W_C[H₂O]

W_C[H₂O] = W_A[CO] + 2W_A[CO₂] + W_B[H₂O] - W_P[CO] - 2W_P[CO₂]

czyli

W_C[H₂O] = 116,7 kmol/h

Natężenie strumienia wodoru w strumieniu P obliczamy z bilansu wodoru.

2W_A[H₂] + 2W_B[H₂O] = 2W_P[H₂] + 2W_C[H₂O]

W_P[H₂] = W_A[H₂] + W_B[H₂O] - W_C[H₂O]

czyli

W_P[H₂] = 67,3 kmol/h

Bilans reaktora przedstawiono w tabeli 6.

Tabela 6. Bilans masy

Przychód, kmol/h	Rozchód, kmol/h
H2 34	H2 67,3
N2 25	N2 25
CO2 4	CO2 37,3
CO 37	CO 3,7
H2O 150	H2O 116,7

Ułamki molowe wodoru, tlenku węgla (II) i tlenku węgla (IV) w strumieniu P wynoszą:

= 0,50

= 0,03

= 0,28

Przykład 7

Stężony kwas siarkowy (95 % mas.) otrzymuje się przez absorpcję SO3 w wieży zasilanej H₂SO₄ o stężeniu b % (strumień C). Strumień C powstaje przez zmieszanie strumienia A (90% H₂SO₄) ze strumieniem D zawierającym kwas siarkowy (90%). Stosunek natężenia strumienia zawracanego D do natężenia strumienia B wynosi n (G_D/G_B = n, kg/h/kg/h). Przyjmując za podstawę bilansu 100 kg 95 % H₂SO₄/h (G_B = 100 kg/h) znajdź zależność pomiędzy stężeniem b % kwasu siarkowego zasilającego wieżę (b % mas.) i n (b = f(n)).

Masy molowe:

H₂SO₄ - 98 kg/kmol

H₂O - 18 kg/kmol

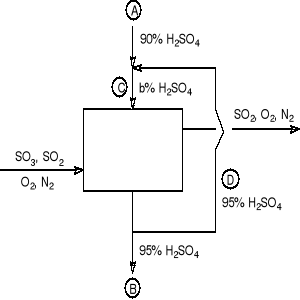
Rozwiązanie

Wodór w strumieniu B pochodzi wyłącznie ze strumienia A (z wody i kwasu). Na podstawie bilansu wodoru (w kg/h) w obszarze zewnętrznym można obliczyć wielkość strumienia A.

0,9G_A ²/₉₈ + 0,1G_A ²/₁₈ = 0,95G_B ²/₉₈ + 0,05G_B ²/₁₈

czyli:

G_A = 84,62 kg/h

W obszarze 1, w którym mieszają się strumienie A i D, w wyniku czego powstaje kwas siarkowy o stężeniu b % (strumień C), przeprowadzamy bilans wodoru:

0,1G_AႷ²/₁₈ +0,9G_AႷ ²/₉₈+0,05G_DႷ²/₁₈+0,95G_DႷ ²/₉₈ = (G_A+G_D)Ⴗ0,01bႷ²/₉₈+(G_A+G_D)Ⴗ(1- 0,01b)Ⴗ²/₁₈

Z definicji n wynika, że:

G_D = G_B Ⴗ n

Ponieważ

G_B = 100 kg/h (przyjęta podstawa bilansu)

a zatem

G_D = 100n

Po podstawieniu G_A = 84,62 kg/h i G_D = 100 n otrzymujemy:

b = (76,158 + 95n)/ (0,8462 + n)

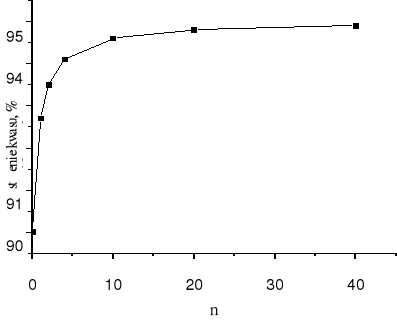
Jeżeli n = 0, na wieżę wprowadza się kwas siarkowy (VI) o stężeniu 90 %. Ze wzrostem n rośnie stężenie wprowadzanego na wieżę H₂SO₄. Dla n → ∞, stężenie kwasu siarkowego wprowadzanego na wieżę dąży do 95 %.

Przykład 8

W procesie półspalania metanu w tlenie powstaje: acetylen, etylen, wodór, para wodna, tlenek i dwutlenek węgla oraz sadza. Gaz po procesie zawiera również nieprzereagowany metan. Całkowity stopień przemiany metanu wynosi 95 %. Stężenie metanu w mieszaninie z tlenem (strumień W_A) wynosi 62 % objętościowych. Uproszczony schemat procesu przedstawiono na rysunku:

Stosunek molowy powstałego tlenku węgla do nieprzereagowanego metanu wynosi 10 (W_E[CO]/W_E[CH₄] = 10). Stopień przemiany metanu w sadzę wynosi 2 % (W_D[C]/W_A[CH₄] = 0,02). Stosunek powstałej w reaktorze pary wodnej do tlenku węgla wynosi 1 (W_D[H₂O]/W_E[CO] = 1).

Przyjmując za podstawę bilansu 100 kmol/s strumienia W_A oblicz zależność ułamka molowego acetylenu (a) w strumieniu W_E od n (n - stosunek molowy wytworzonego acetylenu do sadzy (W_E[C₂H₂]/ W_D[C]= n).

Rozwiązanie

Stężenie metanu w mieszaninie z tlenem (strumień W_A) wynosi 62 % objętościowych. Natężenie strumienia metanu i tlenu w gazie wprowadzanym do reaktora wynosi odpowiednio 62 i 38 kmol/s. Stopień przemiany metanu wynosi 95 % czyli:

= 0,95

czyli:

W_E[CH₄] = 3,1

Ponieważ W_E[CO]/W_E[CH₄] = 10, po podstawieniu otrzymujemy:

W_E[CO] = 31

Stosunek natężenia strumienia pary wodnej (W_D[H₂O]) do natężenia strumienia tlenku węgla (II) (W_E[CO]) wynosi 1, czyli

W_D[H₂O] = 31

Z zależności W_D[C]/W_A[CH₄] = 0,02 otrzymujemy W_D[C] = 1,24

Ponieważ W_E[C₂H₂]/ W_D[C] = n, po podstawieniu otrzymujemy

W_E[C₂H₂] = 1,24n

Natężenie strumienia dwutlenku węgla (IV) obliczamy z bilansu tlenu:

2W_A[O₂] = W_D[H₂O] + W_E[CO] + 2W_E[CO₂]

stąd

W_E[CO₂] = 7

Natężenie strumienia C₂H₄ obliczamy z bilansu węgla:

W_A[CH₄] = W_E[CH₄] + W_D[C] + W_E[CO] + W_E[CO₂] + 2W_E[C₂H₂] + 2W_E[C₂H₄]

czyli

W_E[C₂H₄] = 9,83 - 1,24n

Natężenie strumienia wodoru W_E[H₂] otrzymujemy z bilansu wodoru:

4W_A[CH₄] = 4W_E[CH₄] + 2W_E[C₂H₂] + 4W_E[C₂H₄] + 2W_D[H₂O] + 2W_E[H₂]

W_E[H₂] = 67,14 + 1,24n

Bilans reaktora przedstawiono w tabeli 7.

Tabela 7. Bilans masy

P, kmol/s R, kmol/s

CH₄ 62 CH₄ 3,10

H₂O 31

O₂ 38 C 1,24 C₂H₂ 1,24n CO 31

CO₂ 7

C₂H₄ 9,83 - 1,24n (0 Ⴃn<7,92)

H₂ 67,14 + 1,24n

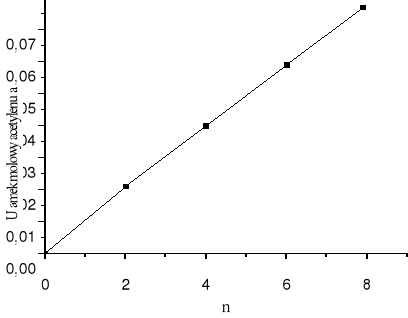
Zależność ułamka molowego acetylenu (a) w strumieniu W_E od n obliczamy ze wzoru:

a =

a =

W_E

CO, CO₂, H₂, CH₄

C₂H₂, C₂H₄

REAKTOR

FILTR

W_A

CH₄, O₂

C (sadza), H₂O

W_D

W_B

---