1. Przedmiot Geodezji.
Geodezja - geōdaisia - nazwa wprowadzona przez Arystotelesa(gē-ziemia, daiomai-dzielę), geodezja jest to nauka o pomiarach Ziemi wykonywanych w celu: -wyznaczenia kształtu i wielkości jej części lub całości, sporządzania map geodezyjnych, wykorzystywania tych pomiarów do rożnych prac inżynierskich i gospodarczych.
Rola geodezji - udział w powstawaniu inwestycji budowlanej, projektowanie aktualny podkład mapy nowy pomiar, pomiar uzupełniający, realizacja opracowanie planu realizacji i sporządzanie szkicu dokumentacji, lokalizacja obiektu, obsługa geodezyjna przy wznoszeniu obiektu], eksploatacja.
Zadania geodezji:
-naukowe- określa kształt i wymiary globu ziemskiego, określa wraz z innymi naukami budowę wnętrza Ziemi.
-praktyczne- wyznaczenie miarowych zależności pomiędzy punktami znajdującymi się na powierzchni Ziemi lub w jej pobliżu. Zależności te powinny być wyznaczane w taki sposób aby można było sporządzić opracowanie graficzne (mapy)
Podział geodezji w zależności od zastosowanej powierzchni odniesienia:
- wyższa- przyjmujemy że Ziemia jest kulą, elipsoidą.
- niższa- przyjmujemy że Ziemia jest płaszczyzną
Geodezja wyższa- zajmuje się wyznaczeniem kształtu i wielkości bryły Ziemskiej, utworzeniem osnowy geodezyjnej jako podstawy do wszelkich pomiarów, prac geodezyjnych.
Geodezja wyższa wiąże się z geologią, geofizyką, są wykonywane pomiary do wyznaczenia wysokości niwelacji precyzyjnej, oznaczenia kierunku linii pomiaru, siły grafometrycznej, siły ciężkości.
Geodezja niższa- na mapie są przedstawione pomiary na ograniczonym obszarze na fizycznej powierzchni Ziemi oraz część obiektów. Są to szczegóły topograficzne.
Szczegóły na mapie:
-osiedla ludzkie (budynki, infrastruktura, szlaki komunikacyjne, budowle w terenie)
- użytki rolne, leśne, sady, kopalnie
- zabytki kultury,
- osobliwości przyrody
-ekstremalne punkty powierzchni
- szczegóły, które nei istnieją w terenie- linie rozgraniczające grunty, linie administracyjne działek, warstwice
W geodezji niższej w zależności od zastosowania dziedziny gospodarki narodowej mamy geodezje gospodarczą:
- inżynieryjno-przemysłowa- pomiary terenów pod budowę dróg, kolei, kanałów, pomiary inwentaryzacyjne, powykonawcze, pomieszczeń budowli.
- górnicza- zajmuje się pomiarami, badaniami geodezyjnymi w związku z poszukiwaniem i wydobywaniem kopalin użytecznych, określeniem wpływu eksploatacji górniczej na powierzchnię terenu, a także obiekty budowlane. Zajmuję się pracami pod powierzchnią i na powierzchni, które są ze sobą związane, projektowanie i budowa tuneli.
- rolna i leśna- pomiary wszelkiego rodzaju urządzenia terenów wiejskich (rolnych i leśnych), scalenie gruntów, wymiana gruntów.
- miejska- pomiary w zakresie postawienia korzenia budowy miast.
Pole informacyjne- przyporządkowanie określonych informacji punktów w czasoprzestrzeni.
Osnowa geodezyjna stanowi usystematyzowany zbór punktów geodezyjnych, utrwalonych w terenie znakami geodezyjnymi, dla których matematycznie określone ich wzajemne położenie i dokładność usytuowania.
Podział pomiarów w geodezji:
pomiary małych obszarów:
sytuacyjne- mają na celu uzyskanie obrazu sytuacji danego terenu (wzajemne rozmieszczanie znajdujących się na nich szczegółów) do pomiarów stosowane są metody poligamizacji i geodezyjnych zdjęć sytuacyjnych, metody pomiarów prostoliniowych (ortogonalna), biegunowa metoda, metoda wcięć kątowych, wcięć liniowych, przecięć, przedłużeń. Przyjmuje się płaszczyznę jako powierzchnie odniesienia.
Wysokościowe (niwelacyjne)- wyznaczenie punktów w terenie na przyjęty poziom odniesienia. Niwelacji podlega wyznaczenie różnicy wysokości. Może być wyznaczona poprzez niwelacje trygonometryczne, hydrostatyczne, geometryczne, barometryczne. W wyniku pomiarów wysokościowych powstaje mapa wysokościowa. Zawiera warstwice (punkty łączące tereny o jednakowej wysokości) pomiar wysokościowy może być stosowany poprzez odbiorniki GPS. Jest wykonywany w kierunku elipsoidy.
Sytuacyjno- wysokościowe- za pomocą tachimetrii-elektroniczna i za pomocą fotogrametrii.
Ze względu na zakres dzieli się na:
Podstawowe- podstawowych osnów geodezyjnych poziome i wysokościowe, magnetyczne, odbiorniki GPS, grawimetryczne.
Szczegółowe- pomiary dotyczące pomiarów sytuacyjnych, wysokościowych oraz rzeźby terenu. Dotyczące pomiarów z wytyczeniem charakterystycznych punktów obiektów realizowanych do projektów (elementy zagospodarowania terenu).
Wykonywany w ramach geodezji przemysłowej- pomiary związane ze ścisłą lokalizacją przestrzenna maszyn przemysłowych (np. turbiny elektronowej).
Ze względu na etapowość:
Polowe
Obliczeniowe
Graficzne (kameralne)
Wielkości podlegające pomiarowi:
- odległość pozioma
- różnica wysokości
- kąt poziomy
- kąt pionowy
- kierunek odniesienia
AB- odległość rzeczywista nachylenia
AoBo- odległość pozioma
BBo- odległość pionowa
L- kąt pionowy
Na mapie są przedstawione odległości zredukowane na poziom.
Odległość pozioma- odległość liczona pomiędzy rzutami tych punktów na płaszczyznę poziomą.
Różnica wysokości- jest to odległość liczona wzdłuż linii pionu, która jest zawarta pomiędzy dwoma punktami równoległymi przechodzącymi przez te punkty.
Kąt poziomy- kąt zawarty pomiędzy rzutami kierunków na płaszczyznę poziomą i liczony w tej płaszczyźnie.
Kąt pionowy- jest to kąt liczony w płaszczyźnie pionowej a rzutem tego kierunku na płaszczyznę.
Kierunek odniesienia- Styczna do południka geograficznego lub magnetycznego przechodzącego przez stanowisko obserwatora.
Błędy przy pomiarach geodezyjnych- odchylenie od wartości pomiarów
Przyczyny błędów:
-instrument
-metoda pomiaru
-warunki środowiska
-dyspozycja obserwatora
Pomiary nadliczbowe- aby zwiększyć dokładność mierzy się kilka razy i liczymy średnią arytmetyczną i błąd.
2. Rola geodezji w budownictwie
Etapy powstawania inwestycji budowlanych
Podkład mapowy
Projekt inwestycji
Geodezyjne opracowanie obiektu
Założenie osnowy realizacyjnej
Tyczenie lokalizacyjne obiektu budowlanego
Tyczenie szczegółów budowli
Obsługa i pomiary kontrolne podczas wznoszenia budowli
Inwentaryzacja powykonawcza
Pomiary przemieszczeń i odkształceń podczas budowy i w czasie eksploatacji.
*pkt 1, 3, 4, 5, 6 -musi wykonać geodeta
*pkt 2, 7, 8, 9- może wykonać kierownik budowy
Udział geodezji w powstawaniu inwestycji budowlanej:
wynikający z definicji geodezji
wykazania na podstawie etapów.
Szkic dokumentacyjny- szkic bez zachowania skali, zawierający osnowę geodezyjna, kierunek północy, obiekty w terenie, obiekt, który będzie wytyczony, wszystkie wymiary do wytyczenia obiektu w terenie.
Projektowanie:
Aktualny podkład mapowy:
-nowy pomiar
-pomiar uzupełniający
Realizacja:
a) geodezyjne opracowanie projektu inwestycji lub zgłoszenie działki i sporządzenie szkicu dokumentacyjnego.
Geodeta musi wykonać ważniejsze obiekty, naroża i osie budowli, określenie współrzędnych.
b) lokalizacja obiektu w terenie (wytyczenie obrysu, osi konstrukcyjnych)
c) obsługa geodezyjna przy wznoszeniu obiektu w terenie:
* tyczenie osi budowli
* pionowanie
* praca kontrolna
- pomiar kontrolny konstrukcji podporowej
- pomiar kontrolny ustawieni elementów konstrukcyjnych
* przeniesienie wysokości na n-tą kondygnację
d) inwentaryzacja powykonawcza
Eksploatacja:
Badanie przemieszczeń (pomiary okresowe)
3. Informacja o mapach, charakterystyka, proces powstawania.
Mapa geograficzna - zmniejszony, matematycznie określony umowny obraz powierzchni terenu przedstawiony na płaszczyźnie, zawierający informację o rozmieszczeniu różnych zjawisk i scharakteryzowany zgodnie z przeznaczeniem każdej mapy. Cechy - zmniejszony, matematycznie określony, umowny, zgeneralizowany, dwuwymiarowy, wymierny.
Skala mapy- jest to stosunek matematyczny odległości „d” między punktami na mapie do odległości „D” na płaszczyźnie odniesienia.
![]()
M - mianownik skali
Skala umożliwia określenie:
- pomiaru odcinków na mapie
- powierzchni
- dokładności danej mapy
Dokładność 1:2000= 0,1mm x 2000= 200mm = 0,2m
- pozwala na określenie różnicy wysokości, współrzędnych geograficznych.
Edycje map zasadniczych wykonuje się w skalach:
1:500
1:1000
1:2000
1:5000 (są to inaczej skale bazowe)
Najmniejszą jednostką obszaru, dla którego określa się skalę bazową mapy zasadniczej zarówno przy postaci klasycznej jak i numerycznej jest obręb ewidencji gruntów i budynków. W wyjątkowo uzasadnionych przypadkach dopuszcza się odmienną skalę dla części obszaru.
Skalę bazową ustala się na podstawie:
stopnia zagęszczenia na mapie elementów stanowiącą jej treść
przewidywanych zamierzeń inwestycyjnych
Jako wytyczne do ustalania skali bazowej przyjmuje się, że niżej wymienione skale powinny być stosowane odpowiednio:
skala 1:500 - dla terenów o znacznym, obecnym lub przewidywalnym zainwestowaniu.
Skala 1:1000 - dla terenów małych miast, aglomeracji miejskich i przemysłowych oraz terenów osiedlowych, wsi będących siedzibami gmin.
Skala 1:2000 - dla pozostałych zwartych terenów osiedlowych, terenów rolnych o drobnej, nieregularnej szachownicy stany władania oraz większych zwartych obszarów rolnych i leśnych na terenie miast.
Skala 1:5000 - dla terenów o rozproszonej zabudowie wiejskiej oraz gruntów rolnych i leśnych na obszarach pozamiejskich.
Podziałka- graficzne przedstawienie skali:
-liniowa
- poprzeczna (transwersalna)
Dokładność podziałki transwersalnej- długość terenowa polowa (terenowa) odpowiadająca wartości najmniejszej działki podziałki.
Znaki umowne- SA przedstawiane graficznie, mogą być jako znaki powierzchniowe ( działki ewidencyjne, działki, budynki) i jako elementy liniowe )drogi, ulice, uzbrojenie terenu) i jako elementy punktowe (latarnie, drzewa) musza być łatwe do zidentyfikowania. Znaki na mapię są dodatkowo uzupełniane za pomocą opisu słownego i liczbowego. Sposób przedstawienia to rzut prostoliniowy szczegółu na płaszczyznę.
Wielkości określane z mapy:
- odległość
- kąt
- współrzędne
- wysokość punktu
- spadek terenu
- różnica wysokości
- linia jednakowego spadku
- profil terenu
- powierzchnie pół: metoda graficzna, analityczna, mechaniczna
Mapa musi być kompletna, aktualna i zgodna z terenem.
Mapa zasadnicza - zgodnie z art. 2, p.7 ustawy z dnia 17 maja 1989 Prawo Geodezyjne i Kartograficzne - jest to wieloskalowe opracowanie kartograficzne zawierające aktualne informacje o przestrzennym rozmieszczeniu obiektów ogólnogeograficznych oraz elementach ewidencji gruntów i budynków, a także sieci uzbrojenia terenu: nadziemnych, naziemnych i podziemnych.
Mapa zasadnicza stanowi:
podstawowy element państwowego zasobu geodezyjnego i kartograficznego w rozumieniu art. 40 ustawy Prawo Geodezyjne i Kartograficzne.
podstawowy materiał kartograficzny, wykorzystywany do zaspokojenia różnorodnych potrzeb gospodarki narodowej, a w szczególności zagospodarowanie przestrzennego.
źródłowe opracowanie kartograficzne do sporządzania map pochodnych i innych wieloskalowych map tematycznych, oraz aktualizacji mapy topograficznej w skali 1:10000 (1:5000).
Mapa zasadnicza służy do celów administracyjnych, prawnych, ewidencyjnych i projektowych oraz stanowi część składową krajowego systemu informacji o systemie.
Mapa tematyczna- opracowanie kartograficzne eksponujące jeden lub kilka wybranych elementów treści mapy ogólno-geograficznej bądź też zagadnienia, zjawiska i procesy społeczno-gospodarcze lub przyrodnicze.
Klasyfikacja map geograficznych:
6mapy ogólno-geograficzne
- topograficzne wielkoskalowe
- topograficzne średnioskalowe
- topograficzne małoskalowe
mapy tematyczne
- społeczno-gospodarcze\
gospodarcze
- mapa zasadnicza
- podstawy zagospodarowania terenu
- uzbrojenie terenu
- komunikacji
- gospodarki mieszanej
- przemysłu
- rolnictwa
- usług
społeczne
- demograficzna
- wybranych elementów socjalno-bytowych
- patologi społecznych
- przyrodnicze
Deformacja mapy- zmiana skali mapy spowodowana zniekształceniem jej podłoża na skutek zmiennych warunków przechowywania, głównie wilgotności i temperatury. Deformacja mapy może być ujeta w dwojaki sposób:
- za pomoca współczynnik deformacji
- deformacji względnej
Deformacja mapy wyraża się w procentach.
Rodzaj podłoża |
Def. wzdłuż włókien w % |
Def. W poprzek włókien w% |
Papier I klasy |
1,0 |
2,5 |
Papier ozalidowy |
5,0 |
12,0 |
Plansza aluminiowa |
0,7 |
0,7 |
Kalka techniczna |
5,0 |
12,0 |
Folia poliestrowa |
0,003 |
0,003 |
Dopuszczalna wielkość współczynnika deformacji:
-do 3% dla odcinka
-do 5% dla powierzchni wykreślonych na mapie.
W przypadku stwierdzenia większych deformacji, celowe może okazać się przetworzenie mapy i doprowadzenie jej do żądanej skali poprzez transformację fotooptyczną.
Spadek terenu- stosunek różnicy wysokości pomiędzy punktami do odległości poziomej tych punktów. Spadek terenu jest równy tangensowi kąta nachylenia terenu.
Warstwica- linia łącząca punkty i jednakowej wysokości.
Skok warstwic- pionowa odległość pomiędzy sąsiednimi warstwicami.
Profil terenu- linia obrazująca rzeźbę terenu wzdłuż obranej trasy lub kierunków do niej poprzecznych, ustalonych na podstawie danych z mapy lub pomiaru w terenie.
Profil zawiera następujące elementy:
-odległości
- rzędne terenu
- poziom porównawczy
- użytkowanie terenu
- skalę
Zapis ![]()
oznacza, że na profilu rzędne terenu SA podane w skali 1:50, a odległości w skali 1:500
Interpolacja warstwic- polega na znalezieniu na linii o jednakowym spadku punktów o zadanych wysokościach i połączeniu punktow o tych samych rzędnych.
W tym celu należy:
- punkty o podanych wysokościach na mapie połaczyć linią prostą;
- wyrysować na kalce technicznej pęk linii równoległych o jednakowych odstępach i opisać wysokościami warstwic jakimi będzie przedstawiona rzeźba terenu.
- wpasować wysokość punktu A pomiędzy odpowiednie linie o pełnych wartościach poprzez przesuwanie kalki z narysowanymi liniami;
- w punkt A wbić szpilkę przez kalkę i obracać nią tak, aby wpasować punkt B;
- zrobić ukłucia w miejscach przecięcia odcinka AB i pęku linii równoległych.
Tak należy postąpić w stosunku do pozostałych spadków, pomiędzy którymi można interpolować. Z kolei połączenie punktów o jednakowych wysokościach wyznaczy przebieg warstwicowy.
4. Odwzorowanie kartograficzne.
Długośc geograficzna- jest to kąt dwuścienny zawarty pomiędzy płaszczyzną przyjętego południka początkowego początkowego płaszczyzna południka przechodzącego przez dany punkt (którego długość chcemy określić)
Szerokośc geograficzna- jest to kąt jaki tworzy kierunek pionu w danym punkcie P (prosta lącząca punkt P ze środkiem kuli 0) z płaszczyzną równika.
Rodzaje powierzchni odniesienia:
Geoida - powierzchnia powstała przez przedłużenie pod lądami i nad depresjami spokojnej powierzchni morza i oceanów (powierzchnia ekwipotencjalna - powierzchnia o stałym potencjale ziemskiego pola grawitacyjnego).
Geoida zerowa - geoida przechodząca przez średni poziom morza wybranej stacji mareograficznej.
Elipsoida trójosiowa - bryła dająca trzy różne elipsy w trzech wzajemnie do siebie prostopadłych przekrojach, której południki są elipsami o jednej osi stałej.
Elipsoida obrotowa spłaszczona - powstaje poprzez obrót elipsy wokół małej osi (elipsoida odniesienia).
Sferoida- elipsoida obrotowa
Siła ciężkości- w każdym miejscu prostopadła do geoidy.
Odwzorowania kartograficzne- przedstawienie obszaru kulistego Ziemi na obraz płaski nazywamy odwzorowaniem kartograficznym.
Kartometryczność mapy ocenia się poprzez porównanie długości odcinka pomierzonego graficznie na mapie zdeformowanej dla poszczególnych odcinków kontrolnych.
Mapa jest kartometryczna gdy deformacja mapy jest mniejsza od wartości dopuszczalnych.
Zadania odwzorowania :
utworzenie obrazu siatki geograficznej - południków i równoleżników ;
wyprowadzenie wzorów matematycznych zależności współrzędnych geograficznych i prostokątnych
Podział odwzorowań:
ze względu na zachowanie pewnych elementów odwzorowywanych figur
wiernokątne (konforemne)
wiernoodległościowe
wernopolowe
dowolne.
ze względu na rodzaj powierzchni odwzorowania, na którą rzutujemy powierzchni odniesienia
płaszczyznowe (azymutalne)
walcowe
stożkowe.
ze względu położenia osi powierzchni odwzorowania względem osi Ziemi
normalne (biegunowe)
poprzeczne (równikowe)
ukośne (horyzontalne)
długość - metr (m)
masa - kilogram (kg)
czas - sekunda (s)
natężenie prądu - amper (A)
temperatura - kelwin (K)
ilość materii - mol (mol)
światłość - kandela (cd)
Jednostką podstawową jest metr
kilometr (km) = 1000m = 103
hektometr (hm) = 100 m = 102
decymetr (dcm) = 0,1 m = 10-1
centymetr (cm) = 0,01 m = 10-2
milimetr (mm) = 0,001m = 10-3
mikron () = 0,000001 m = 10-6
nanometr (nm) = 10-9
angstrem (Ao) = 10-10
ar (a) = 100m2
hektar ( ha) = 100 a = 10 000 m2
kilometr kwadratowy (km2) = 100ha = 1000 000 m2
decymetr kwadratowy (dcm2) = 0,01m2
centymetr kwadratowy (cm2) = 0,0001 m2
milimetr kwadratowy (mm2) = 0,000 001m2
Miary stopniowe
Miary gradowe
Centygrad ( c) = 0,01g
Decymiligrad (cc) = 0,0001g
Miara łukowa
Układ współrzędnych - jest to zespół obiektów geometrycznych, względem których określa się jednoznaczne położenie punktu.
jednowymiarowy
dwuwymiarowy
trzywymiarowy.
Na płaszczyźnie stosujemy:
układ kartezjański (X,Y)
układ biegunowy (ramie bieguna r i kąt biegunowy ).
A
układ kartezjańskie (X,Y,Z)
układy współrzędnych krzywoliniowych (sferycznych, elipsoidalnych)
prostopadła do osi w danym punkcie płaszczyzna równika astronomicznego,
płaszczyzna przechodząca przez kierunek linii pionu w danym punkcie równoległa do chwilowej osi obrotu Ziemi - płaszczyzna południka astronomicznego.
Szerokość geograficzna - astronomiczna -kąt zawarty m/y kierunkiem linii pionu w danym punkcie P a płaszczyzną równika astronomicznego, (0o<<+90o N, 0o<<-90o S)
Długość geograficzna - astronomiczna - jest to kąt dwuścienny zawarty m/y płaszczyznami południków astronomicznych: Greenwich i danego punktu P, (0o<<+180o E, 0o<<-180o W)
szerokość geograficzna geodezyjna (elipsoidalna)- kąt zawarty m/y normalną do elipsoidy w danym punkcie P a płaszczyzną równika geodezyjnego
długość geograficzna geodezyjna (L elipsoidalna) - kąt dwuścienny zawarty m/y płaszczyzną geodezyjnego południka zerowego a płaszczyzną południka geodezyjnego przechodzącego przez dany punkt P.
typ układu
położenia jego początku
orientacji osi współrzędnych
parametry elipsoidy odniesienia.
cztery strefy w pasach południków 15o, 18o, 21o, 24o dla map wielkoskalowych zniekształcenie około +15 cm/km.
jednostkowe odwzorowanie Gausaa - Krügera z południkiem środkowym 19o dla map topograficznych
czterostrefowe odwzorowanie Gausaa - Krügera w pasach 3o dla map wielkoskalowych.
błędy grube (omyłki) - mają dużą wartość liczbową, spowodowane nieuwagą lub omyłką obserwatora,
błędy systematyczne - powstają wskutek działania ustalonych prawidłowości w określonych warunkach pomiaru (instrumentalne, osobowe, środowiskowe),
błędy przypadkowe - mają charakter losowy i są nie możliwe do wyznaczenia lub wyeliminowania ze względu na ich losową zmienność wartości liczbowych oraz znaku. Można zmniejszyć wpływ błędów przypadkowych poprzez wyrównanie - doprowadzając obserwację do wzajemnej matematycznej zgodności z jednoczesnym dokonaniem oceny dokładności po wyrównaniu.
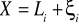
Najbardziej prawdopodobne jest pojawienie się błędów przypadkowych równych zero.
Prawdopodobieństwo błędu mniejszego jest większe niż prawdopodobieństwo błędu większego.
Prawdopodobieństwo błędów o tej samej wartości bezwzględnej lecz o przeciwnych znakach jest jednakowe.
Zwiększenie dokładności pomiaru powoduje zmniejszenie prawdopodobieństwa pojawienia się błędów o dużych wartościach liczbowych.
Przy zwiększeniu ilości obserwacji suma błędów przypadkowych dąży do zera.
Liczba przybliżona- Wynikiem każdego pomiaru są wyniki liczbowe, które wobec nieznanej wartości prawdziwej są liczbami przybliżonymi i ich dokładność jest ograniczona.
0,00345 - 3 cyfry znaczące;
3450 - 4 cyfry znaczące;
0,3145 - 3 cyfry znaczące;
34,5004 - 6 cyfr znaczących
Błąd „krańcowy”(granica błędu) - jest to połowa ostatniej nie napisanej cyfry znaczącej
X - liczba przybliżona
0,70711 - 0,000005 < sin 45o < 0,70711 + 0,000005
Jaki jest błąd krańcowy zapisu liczby (3,14):
wskazują rząd wielkości liczby
charakteryzują dokładność liczby
Jeżeli pierwszą z odrzuconych cyfr jest mniejsza od 5, to liczbę zaokrąglamy „w dół”, pozostawiając ostatnią cyfrę znacząca bez zmian;
Jeżeli pierwsza z odrzuconych cyfr jest większa od 5 - liczbę zaokrąglamy „w górę”, powiększając ostatnią cyfrę znaczącą o jeden;
Jeżeli pierwszą z odrzuconych cyfr jest 5 lecz następuje po niej co najmniej jedna cyfra inna niż zero, to ostatnią pozostawioną cyfrę zwiększamy o 1.
Jeżeli odrzuconą cyfra jest 5 a po niej nie występuję inna cyfra niż zero, to ostatnią pozostawiona cyfrę zwiększamy do najbliższej parzystej.
1233,6545m 1233,65 m ( odległość)
1233,6545 m2 1234 m2 ( powierzchnia)
1233,65450 m 1233,654 m (rzędna wysokości)
1233,654501m 1233,655 m
1233,6535 m 1233,654m
W Polsce obowiązuje układ Gaussa - Krügera konforemny, walcowy, poprzeczny.
Metody wyznaczania powierzchni: w kolejności od najmniej do najbardziej dokładnych:
-kombinowana
- mechaniczna
- graficzna
- analityczna.
5. Jednostki miar stosowane w geodezji i ich przeliczanie.
Jednostka miary- wartość określonej wielkości fizycznej lub innej teoretycznej lub umownej wielkości przyjętej jako jednostka porównawcza do pomiarów wielkości tego samego rzędu.
Wielkość fizyczna- cecha ciała, zjawiska lub pojęcia, którą można mierzyć.
Podstawowe jednostki układu SI:
Miary długości
Metr - odcinek w którym mieści się 1 650 763,73 długości fal świetlnych wysyłanych w próżni przez rozżarzony gaz krypton. Stanowi w przybliżeniu 10-7 ćwiartki południka ziemskiego.
Metr jest to długość drogi przebytej w próżni przez światło w czasie 1/299 792 458 sekundy.
Wielokrotności:
podwielokrotności:
Miary pola powierzchni
Jednostka podstawowa - metr kwadratowy
Jednostki wielokrotności:
jednostki podwielokrotności:
Miary objętości:
Jednostka podstawowa- m3-metr sześcienny
Jednostki wielokrotności
1) kilometr sześcienny = 109 m3
jednostki podwielokrotności
1) decymetr sześcienny- 10-3m3
2) centymetr sześcienny= 10-6m3
3) milimetr sześcienny= 10-9m3
Miary masy:
Jednostka podstawowa- kilogram (kg)
Jednostki wielokrotności\
1) 1 decytona (dt)= 100kg
2) tona=1000kg
Miary kąta
Układ sześćdziesiętny.
Podstawowa jednostka - stopień
1o = 60' = 3600''
Układ dziesiętny.
Podstawowa jednostka - grad (g)
Podwielokrotności:
1g = 100 c = 10 000 cc
Jednostką miary łukowy jest radian (rad lub ρ)
Jest to kąt środkowy oparty na łuku, długość którego równa się jego promieniowi.
Miara analityczna
Kąt wyrażony w mierze łukowej (analitycznej) jest to stosunek luku Kola na którym on się wspiera do przynależnego promienia r.
Jednostka miary jest radian
Radian-kąt plaski środkowy, zawarty pomiędzy dwoma promieniami wycinającymi z okręgu tego koła odcinek łuku o długości równej promieniowej.
Grad- to kąt środkowy wsparty na 1/400 części obwodu koła.
Stopień- kąt środkowy wsparty na 1/360 części obwodu koła.
6. Elementy rachunku współrzędnych
Współrzędne- Wielkości liniowe lub kątowe określające położenie punktu na płaszczyźnie lub dowolnej powierzchni w sposób względny w stosunku do przyjętych za początek układu płaszczyzn lub linii.
Rodzaje układów współrzędnych:
-układ współrzędnych biegunowy (przestrzenny, płaski)
- układ współrzędnych prostokątny (przestrzenny, płaski)
Inny podział układów współrzędnych:
a) trójwymiarowe układy odniesienia
- układ współrzędnych na kuli (geograficzny, prostokątny)
- układ współrzędnych na elipsoidzie (geodezyjny, prostokątny)
b) płaskie układy odniesienia:
-prostokątny
- plaski
B
r
W przestrzeni stosujemy:
Układ globalny (współrzędne naturalne):
Podstawowa oś - chwilowa oś obrotu Ziemi przechodząca przez środek masy Ziemi.
Podstawowe płaszczyzny:
Współrzędne:
W geodezji stosujemy Umowny Układ Ziemski (CTS - Conventional Terrestial System) z początkiem w środku mas Ziemi.
układ współrzędnych geograficznych - geodezyjnych (B, L)
Układ do określenia położenia punktu na elipsoidzie jest układ współrzędnych geograficznych - geodezyjnych (B, L)
Współrzędne:
ETRS, ETRF-89 - europejskie systemy odniesień przestrzennych powierzchnią odniesienia - elipsoida GRS-80 .
ITRS - światowy system odniesień przestrzennych.
Państwowy system odniesień przestrzennych w Polsce.
Geodezyjny układ odniesień określa się poprzez:
W Polsce po 2001r będzie obowiązywało: układ odniesień „EUREF -89”,powierzchnia elipsoidy GRS-80 o parametrach:
Promień równikowy a=6 378 137 m
Spłaszczenie geometryczne p= 1:298,257222101
Ziemska stała grawitacyjna GM=3 986 005*108 m3s-2
Współczynnik dynamiczny kształtu Ziemi j2= 108263*10-8
Prędkość obrotu Ziemi = 7 292 115*10-11 rad s-1.
Obowiązywał:
Układ współrzędnych prostokątnych „1942” - do połowy lat 60, zastosowano odwzorowanie Gaussa -Krügera na elipsoidzie Krasowskiego. Obejmowało dwa podsystemy:
- dwie strefy w pasach południków 15o i 21o dla map małoskalowych i średnioskalowych z zniekształceniem około +59 cm/km
Obowiązuje:
Układ współrzędnych prostokątnych „1965” - od 1968 roku, odwzorowanie quasi-stereograficzne w czterech strefach w 5 strefie (katowicka) zmodyfikowane odwzorowanie Gaussa - Krügera.
Będzie obowiązywał:
Układ współrzędnych „1992” i „2000” - przyjęto dwa nowe systemy odwzorowawcze na elipsoidę GRS 80 :
Azymut - kąt poziomy zawarty między kierunkiem północy a danym kierunkiem linii, ma punkt docelowy mierzony w prawo zgodnie z ruchem wskazówek zegara wystawiony w miejscu obserwacji.
Azymut geograficzny- kąt poziomy zawarty pomiędzy kierunkiem północy geograficznej a dowolnym kierunkiem na cel w terenie liczony zgodnie z ruchem wskazówek zegara.
Azymut magnetyczny- kąt poziomy zawarty pomiędzy kierunkiem północy magnetycznej a dowolnym kierunkiem na cel w terenie liczony zgodnie z ruchem wskazówek zegara.
Azymut topograficzny- kąt zawarty miedzy kierunkiem osi X przyjętego układu współtrzędnych geodezyjnych a drugim kierunkiem, mierzony od osi X zgodnie z ruchem wskazówek zegara.
Czwartak- kąt ostry zawarty miedzy kierunkiem południka (osią X) a kierunkiem lini mierzony w prawo lub w lewo od tej linii.
Zależności między azymutem a czwartakiem
Układ współrzędnych biegunowych płaskich- określa przyjęty na płaszczyźnie punkt początkowy (biegun) O oraz kierunek osi biegunowej OZ. Położenie punktu P wyznaczają w tym układzie dwie współrzędne: r i β
7. Błędy pomiarowe, ich podział, przenoszenie, błąd średni.
Błąd- odchylenie odchylenie od wielkości standardowej.
Miary dokąłdności:
-błąd średni
- błąd przeciętny
- błąd prawdopodobny
- błąd graniczny
-błąd absolutny
-błąd względny
Błąd średni- wskaźnik dokładności w geodezji. Pozwala na ocene dokaldności wykonanej pracy. Rozróżniamy błędy średnie:
- błąd średni pojedynczego spostrzeżenia wyrażony przez błędy prawdziwe określony jest wzorem
m=± 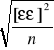
W praktyce stosujemy zazwyczaj błąd średni pojedynczego spostrzeżenia wyrażony przez błędy pozorne
m=± 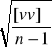
Błąd średni m pozwala ocenić dokładność wykonania poszczególnego, pojedynczego pomiaru, czyli przy kilku pomiarach tej samej wielkości charakteryzuje nam dokładność każdego z nich.
-błąd Średniej arytmetycznej- jeśli mamy n obserwacji (spostrzeżeń) X, np. l1, l2,….ln to najprawdopodoniejsza wartością tej mierzonej wielkości będzie średnia arytmetyczna.
![]()
Średni błąd średniej arytmetycznej jest ![]()
razy mniejszy od błędu średniego pojedynczego spostrzeżenia. Błąd ten pozwala ocenić dokładność przyjętej przez nas najprawdopodobniejszej wartości wyrównanej.
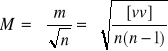
Błąd prawdziwy - różnica miedzy wartością prawdziwą a obserwowaną [![]()
].
Błąd pozorny - różnica między wartością najprawdopodobniejszą[średnia arytmetyczna] a wartością obserwowaną [].Prawdopodobieństwo popełnienia błędu prawdziwego w granicach określonych błędem średnim wynosi 0,68. ![]()
Błąd absolutny - błędy przypadające na całą mierzoną wielkość.
Błąd względny - stosunek absolutnego do wielkości mierzonej, a więc są to błędy przypadające na jednostkę wielkości mierzonej, błędy względne służą do oceny dokładności pomierzonych wielkości.
Błąd prawdopodobny r - jest to błąd którego prawdopodobieństwo przekroczenia równe jest prawdopodobieństwu nieprzekroczenia i wynosi 0,5.
Błąd przeciętny t - jest to średnia arytmetyczna z bezwzględnych wartości błędów pozornych (poprawek) lub błędów prawdziwych:
![]()
![]()
Spostrzeżenie- jest to obserwacj wykonana w celu określenia wartości najprawdopodobniejszej.
Precyzja- stopień doskonałości narzędzia pomiarowego, metod pomiarowych, cecha stała danej metody
doskonałość- stopień najwyższych cech dodatnich.
Źródła błędów w pracach geodezyjnych:
- niedokładność zmysłów obserwatora (wzroku, słuchu)
- niedokładność narzędzi i instrumentów pomiarowych
- warunki środowiska pracy różnie wpływają na wyniki pomiarów (topografia terenu nasłonecznienie temperatura, wilgotność, wiatr itd)
Błędy pomiarowe:
Właściwości błędów przypadkowych - prawdopodobieństwo popełnienia błędu małego jest większe od prawdopodobieństwa popełnienia błędu większego, - liczba błędów ze znakami + równa się w przybliżeniu liczbie błędów ze znakami -, - wystąpienie błędów o tych samych wartościach, lecz o znakach przeciwnych, jest równie prawdopodobne, - wartość błędów nigdy nie przekracza pewnej wartości granicznej.
Prawo błędów Gaussa .
Wartość prawdziwa mierzonej wielkości:
gdzie: X - wartość prawdziwa
Li - obserwacja (spostrzeżenie)
i - błąd prawdziwy
Prawdopodobieństwo występowania błędów przypadkowych - prawo błędów Gaussa - Laplace΄a:
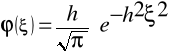
gdzie:
() - funkcja określająca szybkość zmiany prawdopodobieństwa pojawienia się błędu przypadkowego ξ
- przypadkowy błąd prawdziwy
h - parametr związany z warunkami wpływającymi na
dokładność pomiaru
e - podstawa logarytmu naturalnego e= 2,718 281 828...
= 3,141 592 653....
Wnioski na podstawie analizy krzywej Gaussa:
Błąd graniczny- nazywamy największą liczbową wartość błędu dopuszczalną dla danego szeregu spostrzeżeń. Z teorii błędów wynika, że na 1000 spostrzeżeń (dotyczących tej samej wielkości) należy się spodziewac zaledwie 3 spostrezżeń spostrzeżeń błędami większymi od trzykrotnego błędu średniego. Stąd przyjęto uważać trzykrotny błąd średni za błąd graniczny, czyli dopuszczalny
mmax= 3m
błędy większe od błędu granicznego uważa się już za błędy grube .
Prawo przenoszenia się błędów
Błędy wielkości obserwacyjnych powodują, że funkcje tych wielkości też są obarczone błędami (wyrównanie pośredniczących spostrzeżeń).
Dla funkcji nieliniowych:
![]()
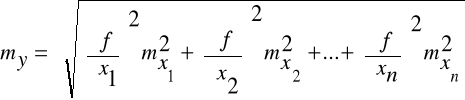
Dla funkcji liniowych:
![]()
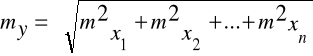
![]()
![]()
Waga- Wagi są to liczby dodatnie, które wyrażają ilość jednakowo dodatnich spostrzeżeń i których użycie pozwala wyznaczyć dokładniej mierzone wielkości.
p1: p2:p3 = n1 : n2 : n3
W praktyce wagę traktuje się jako pewien arytmetyczny wyraz zaufania do danego spostrzeżenia.
Waga II- wagi spostrzeżeń Są to liczby dodatnie odwrotnie proporcjonalne do kwadratów błędów średnich tych spostrzeżeń.
![]()
Często w praktyce stosujemy obie omawiane definicje wag jednocześnie. Ma to miejsce wówczas, gdy przy obserwacjach tej samej wielkości stosujemy instrumenty o różnej dokładności i różna jest liczba obserwacji każdym instrumentem. Wówczas wagi obserwacji każdym narzędziem będą wprost proporcjonalne do liczby obserwacji oraz jednocześnie odwrotnie proporcjonalne do kwadratów błędów średnich tych narzędzi.
![]()
8. Elementy rachunku wyrównawczego.
Przedmiotem rachunku wyrównawczego są obliczenia związane z uzgodnieniem ze sobą wyników pomiarów wykonywanych w większej ilości niż zachodzi potrzeba.
Rachunek wyrównawczy- na podstawie teorii błędów ma zniekształcić wyniki obserwacji α,β,γ poprzez dodanie do niej poprawek v, aby uzyskane (poprawione) rezultaty obserwacyjne spełniały także związki funkcyjne jakie spełniałyby prawdziwe, nieznane wartości mierzonej wielkości.
Lwyr= li+vi
Cel rachunku wyrównawczego- jest zniekształcenie wartości spostrzeżeń, aby je można było uznać za wartości najbardziej prawdopodobne.
Zadania rachunku wyrównawczego-
- wyrównanie spostrzeżeń poprzez dodanie do obserwacji poprawek otrzymanych w toku wyrównania. Poprawki powinny mieć wartość najprawdopodobniejszą.
- określenie dokładności każdego spostrzeżenia oraz dokładności wartości uzyskanych z wyrównania i ich funkcji.
- podanie sposobów kontroli wykonanych obliczeń
- wstępna analiza dokładności projektowanych szczegółów, celem ustalenia warunków potrzebnych do uzyskania założonych dokładności pomiarów lub ich funkcji.
Zasada rachunku wyrównawczego- Prawdopodobieństwo P jednoznacznego pojawienia się błędów v1,v2…vn w przedziałach vi do vi+ dvi równa się iloczynowi poszczególnych prawdopodobieństw. Oznacza to, że:
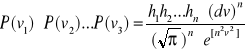
Prawdopodobieństwo iloczynu osiąga maksimum dla
[n2vv] = minimum
Zasada rachunku wyrównawczego
[pvv]= minimum
[pvv]= p1* v12+ p2*v22+…..=min
Suma iloczynów kwadratów poprawek spostrzeżeń i odpowiadających im wag powinna być jak najmniejsza.
Najprawdopodobniejsze wartości mierzonych wielkości uzyska się wtedy gdy błędy podlegające rozkładowi normalnemu będą spełniały warunek [pvv]=minimum
Metoda najmniejszych kwadratów opiera się na prostej recepcie, którą można streścić następująco:
Wynik kolejnego pomiaru xi można uważać za sumę wielkości x(mierzonej) oraz błędu pomiarowego ɛi
xi= x + ɛi
Dobieramy następnie tak wielkości ɛi aby suma kwadratów błędów ɛi była najmniejsza.
![]()
Rodzaje zagadnień wyrównawczych (podział)
a) w zależności od sposobu wyrównania dzieli się na:
- spostrzeżenia bezpośrednie- takie, których najprawdopodobniejsze wartości określa się wprost z rezultatów pomiarów w terenie.
- spostrzeżenia pośrednie- takie gdy inne wielkości podlegały pomiarowi a inne wyrównaniu
- zawarunkowane- takie które musza spełnić warunek
b) pod względem dokładności dzieli się na:
- jednakowo dokładne- gdy będzie ten sam obserwator dokonywał pomiarów lub o zbliżonych umiejętnościach, lub gdy będzie używany do pomiaru jednakowy sprzęt lub o podobnej precyzji, będą te same warunki pomiaru, stosowana ta sama metoda lub o podobnej dokąłdności
Jeżeli choć jeden z warunków będzie zmieniony to będą to niejednakowo dokładne spostrzeżenia (wtedy konieczność wprowadzenia wag)
- niejednakowo dokładne
Wyrównanie obserwacji bezpośrednich.
Wszystkie obserwacje dzielą się na bezpośrednie i pośredniczące.
Obserwacje otrzymane w wyniku porównania wielkości mierzonej z podziałką przyrządu mierniczego podczas wielokrotnych pomiarów tej samej wielkości mierzonej nazywamy spostrzeżeniem bezpośrednim.
Spostrzeżenia, które nie odnoszą się bezpośrednio do wielkości szukanych, lecz służą do wyznaczenia niewiadomych za pomocą ustalonych związków funkcyjnych, nazywamy pośredniczącymi.
10. Ogólne zasady obliczen geodezyjnych. Działanie na liczbach przybliżonych.
Liczba dokładna-Liczba znana z dokładnością nieograniczoną i dająca się zapisać bez błędu nazywa się liczbą dokładną.
V= 4/3 R3 ; M = 1005
Cyfry dziesiętne - wszystkie cyfry położone na prawo od przecinka dziesiętnego.
Cyframi znaczącymi (pewnymi) nazywamy wszystkie cyfry liczby przybliżone, z wyjątkiem zer położonych na lewo od pierwszej różnej od zera cyfry, a także z wyjątkiem wszystkich cyfr niepewnych (obniżonych lub dopisanych drobnym drukiem). Cyfry znaczące określają stopień przybliżenia.
Przykład:
Przeważnie mamy do czynienia z liczbami przybliżonymi o znanym stopniu przybliżenia :
(X0 - x)<X<(X0 + x)
X0 - znane przybliżenie
x - błąd krańcowy (granica błędu)
Zapis błędu krańcowego: ± 5*10-k
Przykład:
0,707105< sin 45o < 0,707115
3,135 < < 3,145
Odpowiedz: ± 5 *10 -3
W zapisie dziesiętnym liczby, zera końcowe mogą mieć dwojakie znaczenie:
Przykład:
100km = 100 000m
x = 0,5 km x = 0,5 m
Prawidłowy zapis: 100 km = 100 * 103 m
Zapis licz niepewnych
- mniejszą czcionką, obniżenie
147,2
-do liczb przybliżonych nie wolno dopisywać zer
- w geodezji ostatnie cyfry są niepewne „w granicach zaokrąglenia dziesiętnego” Oznacza to, że błędy krańcowe nie przekraczają co do wartości bezwzględnej połowy jednostki ostatniego miejsca np. 127, 45m to |Δx| < 0,005m
Reguły zaokrąglenia.
Przykład:
Ocena dokładności funkcji liczb przybliżonych- oszacowanie błędów obliczeń.
a) metody
- podwójnego obliczenia
- wielocyfrowości
- różniczkowa
6
Wyszukiwarka
Podobne podstrony:
geodezja, uczelnia, BL, Geodezja, egzamin
pyt. egzamin07, uczelnia, BL, Geodezja, egzamin
geodezja - egzamin pytania, uczelnia, BL, Geodezja, egzamin
Fotogrametria i teledetekcja 3, uczelnia, BL, Geodezja, zagadnienia z geodezji
Pomiar sytuacyjny metodą domiarów prostokątnych, uczelnia, BL, Geodezja, zagadnienia z geodezji
Obliczanie powierzchni, uczelnia, BL, Geodezja, zagadnienia z geodezji
Niwelacja reperów, uczelnia, BL, Geodezja, zagadnienia z geodezji
Kąt poziomy, uczelnia, BL, Geodezja, ściągi
Kąt pionowy, uczelnia, BL, Geodezja, ściągi
Geodezja-ściąga (3), uczelnia, BL, Geodezja, ściągi
Pytania egzaminacyjne sem.IV.Bud.Og, uczelnia, BL, BO
geodezja sciaga 4, uczelnia, BL, Geodezja, ściągi
Geodezja 10 IŚ, uczelnia, BL, Geodezja, laboratorium
Metoda kierunkowa pomiaru kątów, uczelnia, BL, Geodezja, zagadnienia z geodezji
Fotogrametria i teledetekcja 2, uczelnia, BL, Geodezja, zagadnienia z geodezji
Ćwiczenie 6, uczelnia, BL, Geodezja, ćwiczenia
więcej podobnych podstron