1. Zbiór rozmyty, zbiór normalny, wysokość zbioru

Zbiorem rozmytym A w pewnej (niepustej) przestrzeni X, co zapisujemy jako A ⊆ X, nazywamy zbiór uporządkowanych par

gdzie:

jest to funkcja przynależności zbioru rozmytego A. Funkcja ta każdemu elementowi x ∈ X przypisuje jego stopień przynależności do zbioru rozmytego A, przy czym można wyróżnić 3 przypadki:

1. μ_A(x) = 1 oznacza pełną przynależność do zbioru rozmytego A, tzn. x ∈ A,

2. μ_A(x) = 0 oznacza brak przynależności elementu x do zbioru rozmytego A, tzn. x ∉ A,

3. 0 < μ_A(x) < 1 oznacza częściową przynależność elementu x do zbioru rozmytego A.

Symboliczny zapis zbiorów rozmytych.

Ponieważ niewygodnie jest posługiwać się uporządkowanymi dwójkami zapisywanymi np. w nawiasach, stosuje się zapis symboliczny. I tak, jeżeli X jest przestrzenią o skończonej liczbie elementów, X = {x₁, ..., x_n}, do zbioru rozmytego A określonego na przestrzeni X stosujemy zapis:

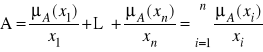
Warto tu zauważyć, że elementami zbioru X mogą być nie tylko liczby, ale również inne przedmioty, osoby lub pojęcia. Zapis ten ma charakter symboliczny. Kreska ułamkowa nie oznacza dzielenia a przyporządkowanie poszczególnym elementom zbioru stopni przynależności. Podobnie znak „+” nie oznacza dodawania, a sumę mnogościową elementów.

Jeżeli X jest przestrzenią o nieskończonej liczbie elementów, to zbiór A ⊆ X symbolicznie zapiszemy jako:

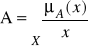
Zbiór rozmyty normalny

Normalnym nazywamy zbiór rozmyty wtedy i tylko wtedy, gdy h(A) = 1. Jeśli zbiór rozmyty A nie jest normalny, to możemy go znormalizować poprzez przekształcenie:

gdzie h(A) jest wysokością tego zbioru.

Wysokość zbioru rozmytego

Wysokość zbioru rozmytego A oznaczamy przez h(A) i określamy jako:

W przypadku zbiorów przeliczalnych jest to maximum funkcji przynależności.

2. Tworzenie populacji początkowej (algorytmy genetyczne) - Przykład

Inicjacja jest to utworzenie początkowej populacji chromosomów, polega na losowym wyborze żądanej liczby chromosomów (osobników) reprezentowanych przez ciągi binarne o określonej długości.

Przykład.

Zgodnie z algorytmem zaczynamy od wylosowania populacji początkowej. Zakładamy, że liczebność naszej populacji będzie wynosić 8 osobników. W wyniku losowania otrzymujemy:

ch₁ = [00110] ch₂ = [00101]

ch₃ = [01101] ch₄ = [10101]

ch₅ = [11010] ch₆ = [10010]

ch₇ = [01000] ch₈ = [00101]

Teraz rozpoczyna się główna pętla algorytmu genetycznego. Najpierw obliczamy przystosowanie poszczególnych osobników. Trzeba zdekodować informacje zawarte w chromosomach, otrzymujemy następujące fenotypy:

ch₁* = 6 ch₂* = 5

ch₃* = 13 ch₄* = 21

ch₅* = 26 ch₆* = 18

ch₇* = 8 ch₈* = 5

Następnie obliczamy wartość funkcji przystosowania, która jest taka sama jak funkcja optymalizowana. Za x podstawiamy wyliczone właśnie fenotypy:

F(ch₁) = 2 ⋅ ch₁ + 1 = 13

F(ch₂) = 2 ⋅ ch₂ + 1 = 11

F(ch₃) = 2 ⋅ ch₃ + 1 = 27

F(ch₄) = 2 ⋅ ch₄ + 1 = 43

F(ch₅) = 2 ⋅ ch₅ + 1 = 53

F(ch₆) = 2 ⋅ ch₆ + 1 = 37

F(ch₇) = 2 ⋅ ch₇ + 1 = 17

F(ch₈) = 2 ⋅ ch₈ + 1 = 11

3. Suma zbiorów rozmytych

Sumą zbiorów rozmytych A i B jest zbiór rozmyty A ∪ B określony funkcją przynależności:

μ_A∪B(x) = max(μ_A(x), μ_B(x)) dla każdego x ∈ X.

Suma większej ilości zbiorów A₁, A₂, A₃, …, A_n określona jest podobną funkcją przynależności:

μ_{A1∪A2∪A3… ∪An} (x) = max(μ_A1(x), μ_A2(x) , μ_A3(x), …, μ_An(x)) dla każdego x ∈ X.

Ilustracja operacji sumy.

Działanie operacji sumy zbiorów rozmytych możemy przedstawić na rysunku:

Rysunek 1. Operacja sumy zbiorów rozmytych.

4. Zbiory rozmyte równe

Zbiór rozmyty A jest równy zbiorowi rozmytemu B, co zapisujemy A = B, wtedy i tylko wtedy, gdy: μ_A(x) = μ_B(x) dla każdego x ∈ X.

5. Poziom równości zbiorów rozmytych

Stopień równości.

Poprzednia definicja jest definicją sztywną. Mamy do czynienia ze zbiorami rozmytymi, dlatego jeśli funkcje przynależności dwu zbiorów rozmytych są podobne, możemy powiedzieć, że zbiory są prawie równe i wprowadzić pojęcie stopnia równości zbiorów rozmytych A i B jako:

gdzie T = {x ∈ X: μ_A(x) ≠ μ_B(x)}.

Nie jest to jedyna możliwość, można spotkać różne definicje stopnia równości lub też stopnia inkluzji zbiorów rozmytych.

6. Wartość bezwzględna liczby rozmytej

Wartość bezwzględną liczby rozmytej A ⊆ R oznaczamy |A| ⊆ R i określamy jako:

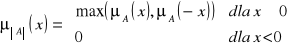
Liczba rozmyta |A| jest liczbą rozmytą dodatnią.

7. Mutacja w algorytmach genetycznych

Mutacja polega na zmianie wartości genu na przeciwną w przypadku binarnego kodu w chromosomach. Zmiany tej dokonuje się dla każdego genu z prawdopodobieństwem mutacji, które jest bardzo małe, dlatego też zachodzi bardzo rzadko.

Możemy np. losować liczbę z przedziału [0, 1] i jeśli jest mniejsza od wartości prawdopodobieństwa mutacji, mutacja zachodzi i zmieniamy wartość genu. Jeśli wylosowana liczba jest większa, mutacja nie zachodzi. Podobnie jak dla krzyżowania.

Wpływ mutacji.

Rozważmy teraz wpływ mutacji. Mutacja zachodzi albo w puli populacji potomków, albo w populacji rodzicielskiej. Możemy zatem rozważać wpływ tej mutacji tylko na pulę rodzicielską, gdyż populacja potomków będzie pulą rodzicielską w następnej generacji, a właśnie o wpływ na pulę rodzicielską nam chodzi.

Operator mutacji zmienia z prawdopodobieństwem p_m zmienia wartość jakiegoś bitu na przeciwną. Jeżeli schemat ma przetrwać mutację, to ustalone pozycje w schemacie, czyli zera i jedynki powinny pozostać niezmienione. Mutacja może zachodzić dla każdego bitu. Prawdopodobieństwo mutacji wynosi p_m, czyli prawdopodobieństwo, że mutacja nie zajdzie to 1 - p_m. Prawdopodobieństwo tego, że mutacja zajdzie na kilku bitach jest iloczynem poszczególnych prawdopodobieństw, a tego, że nie zajdzie też jest odpowiednim iloczynem.

p_m∙ p_m∙ p_m∙ p_m p_m∙…= p_m^L - jest prawdopodobieństwem zajścia mutacji na wszystkich bitach chromosomu.

(1 - p_m) ∙(1 - p_m)…= (1 - p_m)^L - jest prawdopodobieństwem nie zajścia mutacji na wszystkich bitach chromosomu.

Ostatecznie prawdopodobieństwo tego, że mutacja nie zajdzie dla żadnej ustalonej pozycji w schemacie wynosi:

Wniosek 4 - wpływ mutacji.

Dla danego chromosomu ze zbioru M(t) ∩ S, czyli z populacji rodzicielskiej pasującego do schematu S, prawdopodobieństwo, że chromosom ten będzie należał do schematu S po operacji mutacji, jest dane przez

Jest to prawdopodobieństwo przetrwania mutacji przez schemat S.

Wniosek 5 - wpływ mutacji.

Jeżeli prawdopodobieństwo mutacji p_m jest małe, (p_m << 1), to można przyjąć, że prawdopodobieństwo przetrwania mutacji przez schemat S, jest w przybliżeniu równe:

Mutacja.

Operacja mutacji jest dokonywana jest na pojedynczym osobniku. Jako pierwszy mutacji poddawany jest chromosom odchyleń standardowych zgodnie z formułą:

gdzie:

n - długość chromosomu

N(0, 1) - liczba losowa z rozkładu normalnego losowana dla całego chromosomu

N_i(0, 1) - liczba losowa z rozkładu normalnego losowana dla każdego genu osobno

τ', τ - parametry strategii ewolucyjnej

Najczęściej spotykaną postacią tych parametrów jest:

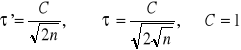
C najczęściej przyjmuje wartość 1.

W ten sposób obliczone nowe zakresy mutacji wpływają na zmianę wartości genów niezależnych x tak jak w poprzedniej strategii:

gdzie znowu N_i(0, 1) jest liczbą losową z rozkładu normalnego.

Mutacja binarna.

Operator mutacji ma za zadanie wprowadzenia pewnego urozmaicenia w populacji. W klasycznym algorytmie genetycznym jego rola jest raczej mała, natomiast w strategiach ewolucyjnych jest on podstawowym operatorem.

W przypadku mutacji binarnej, operacji mutacji podlegały wszystkie geny z założonym bardzo małym prawdopodobieństwem. Mutacja w takim wypadku może polegać na negacji wartości bitu, lub na zamianie wartości bitu na wartość losową.

Mutacja zmiennoprzecinkowa.

Jeżeli chromosom jest kodowany za pomocą liczb rzeczywistych nie można przeprowadzić zwykłej mutacji.

Jeżeli wartość i - tego genu jest ograniczona przedziałem [a_i, b_i], to jeżeli gen podlega mutacji, to przeprowadzamy ją według wzoru:

y_i = a_i + (b_i - a_i)U_i(0,1)

gdzie U_i(0,1) - zmienna losowa wygenerowana z rozkładu równomiernego w przedziale (0, 1).

W tym wypadku nowa wartość genu nie zależy od wartości poprzedniej. Możliwa jest też mutacja, gdzie do starej wartości genu dodajemy losową wartość, najczęściej z rozkładu normalnego.

y_i = x_i + z_i

Inwersja działa na pojedynczym chromosomie zmieniając kolejność alleli pomiędzy dwoma losowymi pozycjami w chromosomie.

Operator ten został zdefiniowany poprzez analogię do biologicznego procesu inwersji chromosomowej, jednak jest on raczej stosowany bardzo rzadko. Jego działanie dla chromosomu przedstawionego niżej z punktami inwersji 4 i 11, wygląda tak:

[0010 1000111 10001] → [0010 1110001 10001]

8. Standardowe funkcje przynależności w Zbiorach rozmytych

Singelton.

W różnych zastosowaniach zbiorów rozmytych używa się standardowych funkcji przynależności. I tak mamy funkcję singelton, zdefiniowaną wzorem:

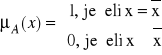
Jest to specyficzna funkcja przynależności, gdyż przyjmuje wartość 1 tylko w jednym punkcie przestrzeni, w pozostałych punktach przyjmuje wartość 0. Ta funkcja charakteryzuje jednoelementowy zbiór rozmyty, jedynym elementem tego zbioru jest punkt x-kreska. Funkcja ta jest stosowana głównie do operacji rozmywania w rozmytych systemach wnioskujących. W sumie jest bardzo podobna do delty Diracka stosowanej w przetwarzaniu sygnałów, która to delta Diracka też przyjmuje wszędzie 0, poza jednym punktem, gdzie ma wartość nieskończoną.

Funkcja Gausowska.

Gausowska funkcja przynależności jest opisana wzorem:

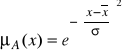
gdzie x-kreska jest środkiem, a sigma określa szerokość krzywej gausowskiej. Ta funkcja jest najczęściej spotykana w różnych zastosowaniach. Wykres funkcji:

Rysunek 2. Gaussowska funkcja przynależności.

Funkcja przynależności typu dzwonowego.

Wzór:

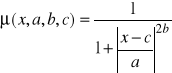
gdzie parametry a, b, c określają wygląd funkcji. a określa szerokość, b nachylenie, c środek. Wykres:

Rysunek 3. Funkcja typu dzwonowego.

Funkcja przynależności klasy s.

Definiujemy ją jako:

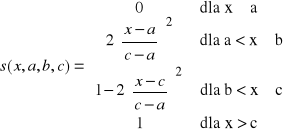
gdzie b=(a+c)/2

Wykres tej funkcji przypomina literę s, stąd jej nazwa. Jej kształt zależy od parametrów a, b, c i w punkcie x = b funkcja przyjmuje wartość 0,5. Wykres:

Rysunek 4. Funkcja typu s.

Funkcja przynależności klasy π.

Tą funkcję przynależności definiuje się poprzez funkcję klasy s:

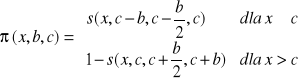
Funkcja ta przyjmuje wartości zerowe dla ­x ≥ c+b oraz x ≤ c - b, natomiast w punktach x = c ± b/2 jej wartość wynosi 0,5. Wykres:

Rysunek 5. Funkcja przynależności typu pi.

Funkcja przynależności klasy γ.

Wzór:

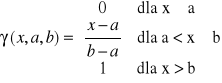
Wykres funkcji gamma jest podobny do wykresu funkcji s.

Rysunek 6. Funkcja typu gamma.

Funkcja przynależności klasy t.

Wzór:

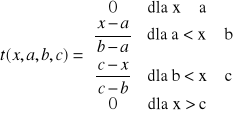
Wykres tej funkcji z kolei jest analogiczny do funkcji klasy pi.

Rysunek 7. Funkcja typu t.

Funkcja przynależności klasy L.

Wzór:

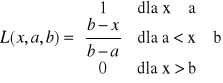
Wykres:

Funkcja klasy Π.

Dotychczasowe funkcje przynależności były określone na przestrzeni jednowymiarowej, jeśli zbiór rozmyty jest określony na przestrzeni wielowymiarowej, to trzeba rozróżnić dwa przypadki. Jeśli poszczególne wymiary są niezależne, to zbiory tworzymy poprzez iloczyn kartezjański oraz korzystamy z jednowymiarowych funkcji przynależności. Drugi przypadek jest wówczas, gdy mamy zmienne zależne. Trzeba wtedy stosować wielowymiarowe funkcje przynależności. Funkcja klasy Π jest zdefiniowana następująco:

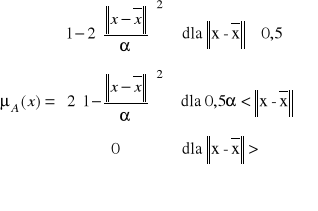
gdzie x-kreska jest środkiem funkcji, a α > 0 określa jej szerokość.

Radialna funkcja przynależności.

Wzór:

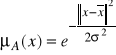
Elipsoidalna funkcja przynależności.

Wzór:

9. operacja Skalowania - liczby rozmyte

W wyniku operacji f(x) = λx, λ ≠ 0, otrzymujemy liczbę rozmytą przeskalowaną w stosunku do liczby rozmytej A ⊆ R. Liczbę tą oznaczamy λA ⊆ R, a jej funkcja przynależności jest równa:

10. Odwrotność liczby rozmytej. Przykład

W wyniku operacji f(x) = x^-1 otrzymujemy liczbę rozmytą odwrotną do liczby rozmytej A ⊆ R. Liczbę tę oznaczamy A^-1 ⊆ R, a jej funkcja przynależności jest równa:

Zakładamy tutaj, że liczba rozmyta A jest albo dodatnia albo ujemna. Jeśli liczba rozmyta nie jest ani dodatnią ani ujemną, to zbiór rozmyty B nie jest wypukły, a więc B nie jest liczbą rozmytą.

Mamy liczbę rozmytą
. Liczba rozmyta:

przeciwna - A :

(1)

odwrotna A^-1:

(2)

Możemy sprawdzić, że
, oraz
. Zatem liczby rozmyte charakteryzują się brakiem liczby rozmytej przeciwnej i odwrotnej względem dodawania i mnożenia, co uniemożliwia np. zastosowanie metody eliminacji do rozwiązywania równań zawierających liczby rozmyte.

przeskalowana ×0,5:

(3)

przeskalowana ×2:

Liczbę rozmytą „mniej więcej 5” możemy zapisać jako:

A = (5, 3, 3)_LP

11. Mnożenie liczb rozmytych

Mnożenie dwu liczb rozmytych A₁ i A₂ oznaczamy

przy czym funkcja przynależności jest określona wzorem wynikającym z zasady rozszerzania przybierającym postać:

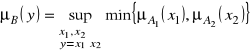
12. Liczby rozmyte - pozostałe działania

Liczby rozmyte

Liczbą rozmytą nazywamy zbiór rozmyty A określony na zbiorze liczb rzeczywistych
A ⊆ R, którego funkcja przynależności:

μ_A: R → [0, 1]

spełnia warunki:

1. sup_x∈μ_A(x) = 1, tzn. zbiór rozmyty A jest normalny,

2. μ_A[λx₁ + (1 - λ)x₂] ≥ min{μ_A(x₁), μ_A(x₂)}, tzn. zbiór A jest wypukły,

3. μ_A(x) jest funkcją przedziałami ciągłą.

Liczby rozmyte.

Na rysunku przedstawione są różne przykłady liczb rozmytych.

Rysunek 8. Przykłady liczb rozmytych.

Liczby dodatnie i ujemne

Liczba rozmyta A ⊆ R jest dodatnia, jeżeli μ_A(x) = 0 dla wszystkich x < 0.

Liczba rozmyta A ⊆ R jest ujemna, jeżeli μ_A(x) = 0 dla wszystkich x > 0.

Na rysunku przedstawiony jest przykład liczby rozmytej dodatniej, ujemnej oraz liczby, która nie jest ani dodatnia, ani ujemna.

Rysunek 9. Liczba dodatnia i ujemna.

Operacje arytmetyczne.

Definicje operacji arytmetycznych są konsekwencją zasady rozszerzania II, w której odwzorowanie przybiera postać:

(4)

Dodawanie dwu liczb rozmytych A₁ i A₂ oznaczamy

przy czym funkcja przynależności jest określona wzorem wynikającym z zasady rozszerzania przybierającym postać:

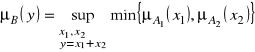
Odejmowanie

Odejmowanie dwu liczb rozmytych A₁ i A₂ oznaczamy

przy czym funkcja przynależności jest określona wzorem wynikającym z zasady rozszerzania przybierającym postać:

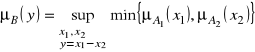
Dzielenie

Dzielenie dwu liczb rozmytych A₁ i A₂ oznaczamy

przy czym funkcja przynależności jest określona wzorem wynikającym z zasady rozszerzania przybierającym postać:

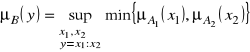
Twierdzenie Dubois i Prade.

Jeżeli liczby rozmyte A₁ i A₂ mają ciągłe funkcje przynależności, to wynikiem operacji arytmetycznych dodawania, odejmowania, mnożenia i dzielenia są liczby rozmyte.

Operacje jednoargumentowe.

Operacje jednoargumentowe przeprowadza się również za pomocą zasady rozszerzania. Jeśli f jest odwzorowaniem f: R → R oraz A ⊆ R, y = f(x), to zgodnie z zasadą rozszerzania mamy:

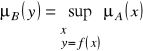
gdzie B = f(A).

Zmiana znaku

W wyniku operacji f(x) = - x otrzymujemy liczbę rozmytą przeciwną do liczby rozmytej A ⊆ R. Liczbę tę oznaczamy - A ⊆ R, a jej funkcja przynależności jest równa:

Liczby rozmyte A i - A są symetryczne względem osi y.

13. Przecięcie zbiorów rozmytych

Przecięciem zbiorów rozmytych A, B ⊆ X jest zbiór rozmyty A ∩ B o funkcji przynależności:

μ_A∩B(x) = min(μ_A(x), μ_B(x))

dla każdego x ∈ X.

Przecięcie większej ilości zbiorów A₁, A₂, A₃, …, A_n określone jest podobną funkcją przynależności:

μ_{A1∩A2∩A3… ∩An} (x) = min(μ_A1(x), μ_A2(x) , μ_A3(x), …, μ_An(x))

dla każdego x ∈ X.

Ilustracja operacji przecięcia.

Działanie operacji przecięcia zbiorów rozmytych możemy przedstawić na rysunku:

Rysunek 10. Operacja przecięcia zbiorów rozmytych.

14. Eksponenta liczby rozmytej.

Operacja eksponent. W wyniku operacji f(x) = e^x, x > 0, otrzymujemy potęgę liczby rozmytej A ⊆ R. Liczbę tą oznaczamy e^A ⊆ R, a jej funkcja przynależności jest równa:

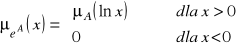
Liczba rozmyta e^A jest liczbą rozmytą dodatnią.

x

μ_A(x)

μ_B(x)

x

μ_A(x)

μ_B(x)

---