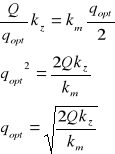ZAOPATRYWANIE W CZĘŚCI ZAMIENNE I MATERIAŁY EKSPLOATACYJNE

System zaopatrywania systemu eksploatacji

Procesy zaopatrywania stanowią istotną fazę procesów logistycznych zapewniających zasilanie systemów eksploatacji w energię i materiały niezbędne do ich funkcjonowania.

Dla systemów eksploatacji maszyn rozważać można procesy zaopatrywania w całe maszyny, części wymienne oraz materiały eksploatacyjne i techniczne, niezbędne w procesach użytkowania i obsługiwania maszyn w aspekcie planowania optymalnych wielkości zapasów.

Zgodnie z zasadami prakseologicznego modelowania działania człowieka proces zaopatrywania jest realizowany w systemie zaopatrzenia poprzez odpowiednie łańcuchy działania

Łańcuch działania procesu zaopatrywania składa się z:

- dostawcy,

- przedmiotu zaopatrywania,

- odbiorcy.

Przedmiotem zaopatrywania mogą być:

- całe maszyny służące odnowie lub powiększeniu potencjału eksploatacyjnego (systemu użytkowania, operacyjnego) parku maszyn

- maszyny obsługowo-naprawcze i narzędzia służące odnowie lub powiększeniu potencjału produkcyjnego bazy obsługowej systemu eksploatacji

- części zamienne (elementy, które można zastosować w maszynie zamiast analogicznych uszkodzonych lub zużytych) służące odnowie potencjału konkretnych maszyn

- materiały eksploatacyjne (substancje potrzebne do prawidłowego działania maszyn, np. paliwa, oleje, smary, płyny chłodnicze, hydrauliczne, hamulcowe itp.) służące zapewnieniu ciągłości procesu użytkowania maszyn

- materiały techniczne (farby, środki konserwujące, kleje, środki czystości, materiały warsztatowe (ślusarskie, spawalnicze, stolarskie itd.) służące realizacji procesu obsługi maszyn

System zaopatrywania tworzy odpowiednia baza (zbiór komórek organizacyjnych) oraz relacje występujące między jej elementami i określające strukturę systemu. Struktura systemu zaopatrzenia powinna być dostosowana do struktury i potrzeb systemu eksploatacji. W zależności od sposobu wzajemnego przyporządkowania elementów struktury systemów eksploatacji i zaopatrzenia wyróżnia się struktury:

- terytorialne - o przyporządkowaniu ściśle związanym z miejscem rozlokowania elementów systemu eksploatacji (zaopatrywanie wszystkich odbiorców znajdujących się na określonym obszarze);

- funkcjonalne - związane z relacjami organizacyjnymi w systemie eksploatacji (zaopatrywanie tylko przydzielonych odbiorców);

- mieszane.

Wybór struktury systemu zaopatrywania (głównie rozmieszczenia źródeł zaopatrzenia względem ośrodków eksploatacji) może także stanowić ważny problem optymalizacyjny rozwiązywany pod kątem minimalizacji czasu lub kosztów transportu związanego z zaopatrywaniem.

Otoczenie systemu zaopatrzenia stanowią:

- system produkcji, który jest dla niego systemem zabezpieczenia

- system eksploatacji maszyn, który jest dla niego przedmiotem działań operacyjnych.

Stąd też, celem działania systemu zaopatrzenia jest zapewnienie prawidłowości i ciągłości działania systemu eksploatacji. Podstawowymi cząstkowymi zadaniami stanowiącymi składowe zaopatrywania są:

- gromadzenie (pozyskiwanie od producentów lub sprzedawców) zapasów;

- utrzymywanie (przechowywanie i magazynowanie) zapasów;

- dystrybucja (rozdzielanie i dostawa do odbiorców, np. stanowisk obsługowo-naprawczych, lub do innych magazynów) zapasów.

Kryteria optymalizacji zaopatrywania

Istnienie zapasów jest zjawiskiem niepożądanym w sensie gospodarczym (koszty gromadzenia i utrzymania elementów w danej chwili zbędnych w systemie eksploatacji), jednakże w wielu dziedzinach działalności człowieka, w tym także i eksploatowaniu maszyn o zadanym odpowiednio wysokim bezpieczeństwie, nieuniknionym. Konieczność gromadzenia zapasów przedmiotów zaopatrywania jest bezpośrednim wynikiem na ogół losowego zużywania maszyn oraz braku możliwości dostarczania odpowiednich przedmiotów zaopatrywania w chwili, w której powstaje na nie zapotrzebowanie.

Konsekwencją celu działania i zadań zaopatrywania jest występująca w systemach zaopatrywania tendencja zwiększania zapasów. Czynnikiem podstawowym przeciwdziałającym gromadzeniu nadmiernej ilości zapasów, są koszty ich utrzymywania oraz straty jakościowe i ilościowe podczas przechowywania.

Biorąc pod uwagę wielkość i potrzebę gromadzenia zapasu można wyróżnić:

• zapas prawidłowy - zapas ekonomicznie uzasadniony, zgodny z potrzebami systemu pod względem ilości i struktury asortymentowej;

• zapas nieprawidłowy - zapas ekonomicznie nieuzasadniony pod względem ilości (nazywamy zapasem nadmiernym) i struktury asortymentowej (zapas zbędny).

Uwzględniając inne kryteria klasyfikacyjne można dokonać podziału zapasów na:

- zapasy początkowe, bieżące, rezerwowe, sezonowe;

- zapas minimalny, średni, maksymalny.

Ustalenie właściwych wielkości zapasów powinno następować w oparciu o strukturę systemu, wielkości zapotrzebowań i dostaw, rachunek kosztów, możliwości transportowe przemieszczania zapasów, itp. Dla określenia wielkości zapotrzebowań części wymiennych i materiałów eksploatacyjnych niezbędna jest znajomość zadań wykonywanych przez system eksploatacji.

Najważniejszy z ekonomicznego punktu widzenia element analizy efektywności działania systemów zaopatrzenia stanowią koszty. Przyjmując jako kryterium klasyfikacji miejsce powstawania kosztów wyróżnia się następujące ich rodzaje:

1. koszty zamówień - związane z kosztami realizacji czynności prowadzących do oceny wielkości zapotrzebowań i przygotowania zamówień. Istnieje część stała i zmienna tej grupy kosztów, niezależna i zależna od wielkości zapotrzebowań;

2. koszty transportu - związane z koniecznością transportowania zapasów. Można również wyodrębnić ich część stałą (utrzymanie pojazdów - środków transportu, płace kierowców i operatorów) i zmienną związaną z ilością wykonanej pracy przewozowej i przeładunkowej (zużycie resursów, koszty paliw, itp.);

3. koszty utrzymania zapasu o następujących składowych:

- koszty finansowania - obejmujące środki finansowe przeznaczone na zakup części i materiałów stanowiących zapasy;

- koszty magazynowania - związane z utrzymaniem bazy magazynowej i personelu magazynów;

- koszty starzenia - zależne od wielkości strat części wymiennych i materiałów w czasie przechowywania;

4. koszty braku zapasu - są to koszty powstające w systemie eksploatacji maszyn lub systemach zabezpieczanych przez system eksploatacji wywołane przez skutki przestoju maszyn i nie wykonania określonych zadań operacyjnych z powodu braku części zamiennych lub materiałów eksploatacyjnych.

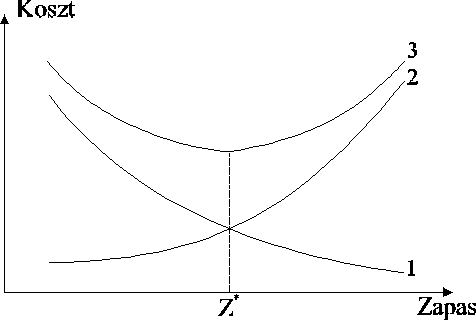
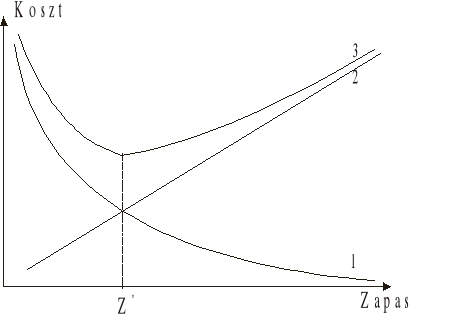
Decydujący wpływ na efektywność działania systemu mają koszty utrzymania i koszty braku zapasu. Ich zależność od poziomu (wartości) zapasu średniego przedstawiono obok. Z przedstawionych zależności wynika, że w oparciu o analizę kosztów można tak określić wielkość zapasu średniego Z*, aby koszt całkowity osiągnął wartość minimalną

1 - koszt braku zapasu; 2 - koszt utrzymania zapasu; 3 - całkowity koszt zaopatrywania

Na sprawność i poprawność działania systemu zaopatrywania ma wpływ szereg ograniczeń, które można podzielić na:

• informacyjne - związane z brakiem informacji w zakresie rzeczywistych zapotrzebowań odbiorców lub obiegiem informacji między systemem zaopatrywania a jego otoczeniem;

• zasileniowe - związane z ograniczeniem przepływu środków finansowych lub materiałowych.

Stąd budowa dokładnego modelu matematycznego opisującego system zaopatrywania i uwzględniającego wszystkie występujące w nim zależności jest praktycznie niemożliwa. Brak jest uniwersalnej metody pozwalającej kompleksowo rozwiązywać problemy zaopatrywania.

Istniejące metody planowania zapasów można podzielić na:

1. metody statystyczne - planowane wielkości zapasów wyznaczane są na podstawie danych z ubiegłych okresów. Zakłada się, że procesy eksploatacji powtarzają się cyklicznie. Metody statystyczne charakteryzuje znaczna prostota obliczeń, jednakże otrzymywane wyniki obarczone są znacznym błędem;

2. metody techniczne - wielkości zapasów obliczane są na podstawie założeń technicznych, np. intensywności zużycia materiałów i zużycia części wymiennych oraz intensywności eksploatacji dla okresu planowania, od których zależne jest zużycie części zamiennych i materiałów eksploatacyjnych. Metody te nie uwzględniają czynników losowych zakłócających działanie systemu eksploatacji jak i systemu zaopatrywania. Charakteryzuje je znaczna pracochłonność procesu planowania i błędy w przewidywaniu zapotrzebowań;

3. metody techniczno-ekonomiczne - przy ustalaniu poziomu średniego zapasów lub wielkości partii dostaw uwzględniane są, poza założeniami technicznymi, także czynniki ekonomiczne;

4. metody statystyczno-analityczne - podstawę do obliczeń stanowią założenia techniczno-ekonomiczne oraz dane o wielkościach zapotrzebowań w okresach ubiegłych. Mogą być traktowane jako połączenie metod wyżej przedstawionych.

W procesie zaopatrywania magazyn może być traktowany jako tzw. element sumujący dynamicznie. Wielkość zapasu w chwili t wyraża się zależnością

gdzie: - Z₀ - zapas początkowy w chwili t = 0;

- q_i(t_i) - strumień dostaw zaopatrzenia do magazynu w kolejnych chwilach czasu t_i w przedziale od 0 do t;

- y_j(t_j) - strumień zrealizowanych zapotrzebowań odbiorców (zapasów zaopatrzenia wydanych z magazynu) w chwilach czasu t_j w przedziale od 0 do t.

Każdy z wymienionych strumieni dostaw i zrealizowanych zapotrzebowań może być:

• ciągły: zmienny lub stały;

• dyskretny: regularny lub nieregularny (ze względu na odstępy czasu między kolejnymi dostawami) oraz stały lub zmienny (ze względu na wartość jednorazowej dostawy do magazynu);

• zdeterminowany lub losowy.

W oparciu o powyższą klasyfikację strumieni można zbudować 144 podstawowe modele procesów zaopatrywania.

Metody wyznaczania optymalnych wielkości zapasów

Metoda Wilsona i jej modyfikacje

Metoda Wilsona, opracowana w 1915 roku przez F.W. Harris'a, jest klasyczną metodą teorii zapasów. Dotyczy przypadku, gdy strumienie dostaw i zapotrzebowań na określony asortyment są zdeterminowane i mają parametry stałe. W modelu zaopatrywania przyjmuje się następujące założenia:

• zużycie asortymentu jest ciągłe i równomierne w czasie;

• wielkość jednorazowej dostawy q jest stała;

• dostawa realizowana jest w chwili gdy poziom zapasu w magazynie osiąga wartość zero;

• kolejne dostawy następują w jednakowych odstępach czasu τ;

• średni zapas asortymentu w magazynie jest równy
  ;

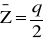
• koszt zaopatrywania w okresie T jest sumą kosztów zamówień i kosztów magazynowania;

• jednostkowy koszt zamówienia jest stały i niezależny od wielkości zamówienia i jest równy k_z;

• jednostkowy koszt magazynowania jest równy k_m.

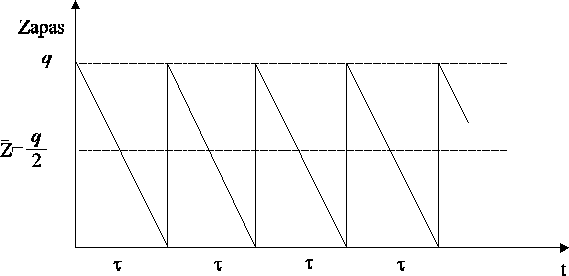
Zależność wartości zapasu w magazynie od czasu dla modelu Wilsona.

Podstawowym zadaniem dla modelu jest wyznaczenie wartości jednorazowej dostawy q na podstawie analizy kosztów zaopatrywania. Załóżmy, że sumaryczne zapotrzebowanie na dany asortyment w okresie T wynosi Q. Zgodnie z przedstawionymi założeniami modelu:

- liczba partii dostaw w okresie T jest równa

- koszt zamówień w okresie T wynosi
(jest hiperboliczną, malejącą funkcją wielkości dostawy)

- koszt magazynowania jest proporcjonalny do poziomu zapasu średniego i wynosi
(jest liniową, rosnącą funkcją wielkości dostawy)

- całkowity koszt zaopatrywania w okresie T wyraża się zależnością

W celu określenia wielkości dostawy, dla której koszty zaopatrywania są najmniejsze, wyznaczamy pierwszą pochodną kosztów całkowitych i przyrównujemy jej wartość do zera:

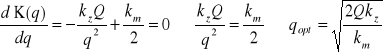
albo porównujemy koszty zamówień 1 i magazynowania 2:

Model Wilsona mimo przyjęcia znacznych uproszczeń procesu zaopatrywania znajduje praktyczne zastosowania do chwili obecnej. Zwiększenie dokładności obliczeń jest możliwe dzięki bardziej precyzyjnemu określeniu kosztów zamówień i kosztów magazynowania poprzez wyodrębnienie:

• części stałej k_z0 i zmiennej k_z1 kosztów zamówień (niezależnej i zależnej od wielkości dostawy). Wówczas całkowity koszt zamówień jest równy
  

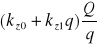
• części stałej k_m0 i części zmiennej k_m1 kosztów jednostkowych magazynowania (niezależnej i zależnej od zapasu średniego). Wtedy koszt magazynowania jest równy
  

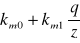
Całkowite koszty zaopatrywania można wyrazić zależnością

Stąd można wyznaczyć wartość dostawy zapewniającej minimum kosztów zaopatrywania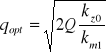

Optymalna wielkość dostawy zależy tylko od części stałej kosztów zamówienia k_z0 oraz zmiennej części kosztów magazynowania k_m1.

Jako modyfikacje metody Wilsona pozwalające na dostosowanie jej założeń do losowego charakteru zapotrzebowania na części wymienne i materiały eksploatacyjne mogą być rozpatrywane:

- metoda stałej wielkości zamówień;

- metoda stałego cyklu zamawiania.

Metoda stałej wielkości zamówień polega na zamawianiu kolejnych dostaw o stałej wielkości q w chwilach, gdy zapas w magazynie zmniejszy się do wartości zapasu minimalnego Z_min. Zapas minimalny powinien z żądanym prawdopodobieństwem zapewnić zaspokojenie potrzeb odbiorców w okresie między złożeniem zamówienia a dostawą. Powinien być dostosowany do warunków, w których występuje maksymalna intensywność zapotrzebowania i najdłuższy czas między chwilą złożenia zamówienia a chwilą nadejścia dostawy:

Z_min = D_max T_max

D - prognozowana intensywność zapotrzebowania odbiorców, np. zapotrzebowanie dzienne

T = t_d - t_z - czas realizacji zamówienia - przedział czasu między chwilą złożenia zamówienia t_z i chwilą nadejścia dostawy t_d

lub

Z_min = D T' + Z_r

T' - średni czas realizacji zamówienia

= - zapas rezerwowy (bezpieczeństwa)

k - współczynnik bezpieczeństwa

d - średni błąd prognozy intensywności zapotrzebowania odbiorców

Wyznaczenie odpowiedniego poziomu Z_min ma tu znaczenie zasadnicze.

Zależność wartości zapasu w magazynie od czasu dla modelu Wilsona dla stałej wielkości zamówień.

Wielkość jednorazowej dostawy może być określona na podstawie modelu Wilsona. Aby nie występował brak zapasów powinien być spełniony warunek: q > Z_min.

Zaletą tej metody jest jednorazowe, dla dostatecznie długiego przedziału czasu, wyznaczenie wartości zapasu minimalnego Z_min i wielkości dostawy q.

Wadą jest konieczność stałej kontroli poziomu zapasu lub jego podziału na dwie części (wyodrębnienie Z_min) w celu określenia chwili złożenia kolejnego zamówienia.

Możliwość sterowania chwilą składania zamówienia pozwala na uwzględnianie wpływu losowych wahań popytu na poziom zapasu w magazynie.

Metoda stałej długości cyklu zamawiania polega na przyjęciu stałego odstępu czasu między chwilami składania kolejnych zamówień, nazywanego cyklem zamawiania T_c. W kolejnych cyklach zamawia się taką ilość asortymentu jaką zużyto w poprzednim cyklu zamawiania. W metodzie tej należy wyznaczyć wielkość zapasu maksymalnego Z_max, który zabezpiecza z żądanym prawdopodobieństwem zapotrzebowanie odbiorców w okresie przyjętego cyklu zamawiania. Zapas maksymalny wyznacza się dla warunków, w których występuje maksymalna intensywność zapotrzebowania z uwzględnieniem nieregularności dostaw:

Z_max = D_max [T_c + (T_max - T_min)]

D - prognozowana intensywność zapotrzebowania odbiorców, np. zapotrzebowanie dzienne

T_c - długość cyklu zamawiania

T = t_d - t_z - czas realizacji zamówienia - przedział czasu między chwilą złożenia zamówienia t_z i chwilą nadejścia dostawy t_d

lub

Z_max = D (T_c + T') +

T' - średni czas realizacji zamówienia

k - współczynnik bezpieczeństwa

d - średni błąd prognozy intensywności zapotrzebowania odbiorców

Zależność wartości zapasu w magazynie od czasu dla modelu Wilsona dla stałej długości cyklu zamawiania

W metodzie tej może być także wyznaczony zapas minimalny - pozwoli to zminimalizować ryzyko powstania braku zapasu.

Metoda stałego cyklu zamawiania wymaga każdorazowego obliczania wielkości zamówienia. Kolejne dostawy są równe q(t_z) = Z_max - Z(t_z), gdzie Z(t_z) jest wielkością zapasu w magazynie w chwili t_z składania zamówienia.

Metoda ABC planowania zapasów

Zazwyczaj magazyn jako element systemu zaopatruje odbiorców w różne części wymienne lub materiały. W przypadku dużej liczby asortymentów dokładne planowanie wielkości zapasów każdego z nich jest praktycznie niemożliwe. Często w takich przypadkach dla wielu asortymentów wykonuje się obliczenia przybliżone, przyjmując orientacyjnie wskaźniki dla procesu zaopatrywania.

Metoda ABC podaje pewne zasady postępowania w przypadku planowania zapasów wielu asortymentów. Dokonuje się podziału wszystkich asortymentów na trzy grupy według kryterium udziału asortymentu w ogólnej ilości i wartości zapasów. Sposób i dokładność planowania zapasu danego asortymentu jest zależna od tego, w której z trzech grup dany asortyment się znajduje.

Podział asortymentów zapasów na grupy A, B, C:

a) udział ilościowy, b) udział wartościowy

asortymentów w ogólnej ilości zapasów

Grupa A - pozycje asortymentowe stanowiące 5 - 10% ogólnej ilości zapasu i wyczerpujące 70 - 80% wartości zapasu. Wymagają one szczególnie dokładnego planowania i kontroli. Ustalana się dla nich indywidualne normy ilościowe, wyrażone w jednostkach miar właściwych dla danego asortymentu.

Grupa B - pozycje asortymentowe stanowiące około 20% ogólnej ilości zapasu i wartości zapasu. Opracowuje się dla nich wartościowe normy grupowe lub grupowe wskaźniki zapasu. Normy wartościowe wyrażane są w jednostkach finansowych. Wskaźniki zapasu są to czasowe normy zapasu wyrażane w jednostkach czasu, np. ilość dni przeciętnego zużycia na które planowany zapas powinien wystarczać. Grupy asortymentów, których dotyczą wymienione normy i wskaźniki ustalane są zwykle według branż - gałęzi materiałowych.

Grupa C - pozostałe pozycje asortymentowe stanowiące 70 - 80% ogólnej ilości zapasu i 5 - 10% wartości zapasu. Wymagają najmniej dokładnego planowania wielkości zapasu. Ustala się dla nich wspólny wskaźnik zapasu, wyrażany w jednostkach czasu i zbiorczą normę zapasu wyrażoną wartościowo.

Metoda ABC może być stosowana w warunkach, gdy znane są wielkości zapotrzebowań w ubiegłych okresach planowania (w celu dokonania podziału) i jest szczególnie przydatna, gdy zapas różnych asortymentów jest zużywany w sposób zdeterminowany, stały (zapotrzebowanie ma jednakową intensywność).

Metody statystyczne planowania zapasów

Zapotrzebowanie na części zamienne i materiały eksploatacyjne ma najczęściej charakter losowy w związku z losowym przebiegiem procesów eksploatacji, stąd dla wyznaczania zapasów stosuje się metody uwzględniające ten fakt. Podstawę do określania zapotrzebowania stanowią dane o zużyciu asortymentów w okresach ubiegłych. Podstawowymi parametrami charakteryzującymi zapotrzebowanie jako proces stochastyczny są wartość oczekiwana (średnia) i odchylenie standardowe wielkości zapasów i zapotrzebowań.

Wartość oczekiwaną zapotrzebowania E(Y) można wyznaczyć z zależności

gdzie: y_i - znana wartość zapotrzebowania w i-tym okresie;

p_i - prawdopodobieństwo, że wartość zapotrzebowania jest równa y_i.

Odchylenie standardowe jest miarą rozproszenia (dyspersji) zapotrzebowania od wartości średniej:

Wartość p_i szacuje się jako prawdopodobieństwa w sensie częstości względnych na podstawie ilości obserwacji n_i, w których wystąpiło zapotrzebowanie o wartości y_i:

gdzie n jest ilością znanych obserwacji zapotrzebowania.

Jeżeli każdą z wartości y_i obserwowano jeden raz, wówczas wartość oczekiwaną i odchylenie standardowe obliczamy jako średnie z n obserwacji:
i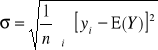

W najprostszym przypadku, wykorzystując dane statystyczne, wielkość zapasu można określić na poziomie wartości średniej: Z = Y₁ ⋅ t_n

gdzie: - Y₁ - średnie zużycie jednostkowe asortymentu (w jednostkowym czasie, np. dzień, miesiąc itp);

- t_n - czas normowania zapasu (liczba dni, miesięcy).

Jeżeli znany jest rozkład prawdopodobieństwa wielkości zapotrzebowań, to na podstawie własności dystrybuanty można określić taką normę zapasu, która z żądanym prawdopodobieństwem zapewni spełnienie zapotrzebowania odbiorców: F(y) = P{Y < y}

Równoczesna możliwość wyznaczenia poziomu zapasu i wartości wymienionego wyżej prawdopodobieństwa jest podstawową zaletą metod statystycznych. W przedstawionej formie są one przydatne, gdy wartość średnia zapotrzebowania odbiorców w dostatecznie długim czasie jest stała.

Do grupy metod statystycznych należy też wykorzystanie teorii masowej obsługi w procesach planowania zapasów. Może być ona wykorzystana w tym aspekcie jedynie na najniższym, podstawowym szczeblu zaopatrywania. W procesie zaopatrywania jako kolejkę można traktować maszyny oczekujące na części wymienne lub materiały eksploatacyjne a także zapas asortymentu w stanie oczekiwania na zużycie. Teorię masowej obsługi można zastosować jeśli charakterystycznym parametrom systemu obsługi: λ (intensywności zgłoszeń do obsługi),
(intensywności obsługi zgłoszeń) i n (liczbie kanałów obsługi) przyporządkujemy odpowiednie parametry procesu zaopatrywania. Przyjmujemy zatem, że:

1. zapasowa część zamienna jest traktowana jako kanał obsługi;

2. strumień zapotrzebowań użytkowników na części zamienne odpowiada strumieniowi zgłoszeń do obsługi;

3. jako czas obsługi τ przyjmujemy czas, w którym zostanie zrealizowane zapotrzebowanie.

Planowanie zapasu części zamiennych metodami teorii masowej obsługi jest analogiczne jak projektowanie liczby stanowisk systemu obsługi i powinno przebiegać według tych samych procedur.

Metoda wyrównywania wykładniczego

Metody statystyczne nie mogą być bezpośrednio stosowane, jeśli średnie zapotrzebowanie na dany asortyment jest zmienne w czasie. Można wyróżnić trzy podstawowe składowe zależności zapotrzebowania na dany asortyment jako funkcji czasu:

1. wahania losowe - zmiany wielkości zapotrzebowania w krótkich przedziałach czasu (np. dzienne) wynikające z działania czynników losowych i wyrażające stochastyczny charakter procesów zużycia części zamiennych i materiałów;

2. wahania okresowe - zmiany wielkości zapotrzebowań występujące w dostatecznie długich okresach czasu, związane są najczęściej z porami roku lub działaniem innych powtarzanych cyklicznie czynników;

3. trend - zmiany średniej wartości zapotrzebowania występujące w długich okresach czasu (miesiące, lata).

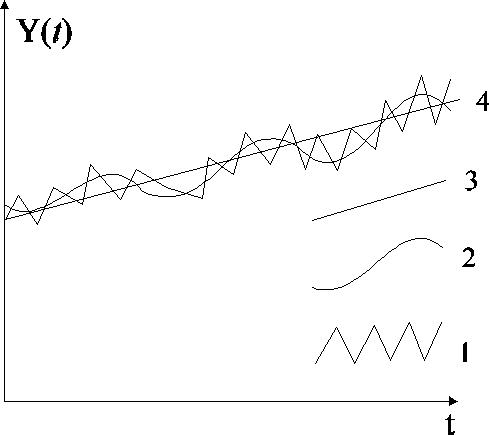
Składniki zapotrzebowania na asortyment części wymiennych lub materiałów:

1) wahania losowe, 2) wahania okresowe, 3) trend, 4) zależność zapotrzebowania od czasu.

Sumaryczny przebieg zapotrzebowania uzyskuje się więc w wyniku syntezy jego trzech składowych. Metoda wyrównywania wykładniczego pozwala uwzględnić istniejące trendy zapotrzebowania poprzez wyznaczenie i przyporządkowanie pewnych współczynników wagowych a_i wartościom realizowanych zapotrzebowań odbiorców z ubiegłych okresów, przy czym
. Współczynniki wagowe determinują wpływ kolejnych okresów poprzednich na planowaną wielkość zapasu w okresie planistycznym. Planowaną wielkość zapasu V można wyrazić ogólną zależnością:

gdzie - V_j - planowane wielkości zapasów dla okresu j;

- Y_i - rzeczywiste, zaobserwowane zapotrzebowanie odbiorców w okresie i.

W celu wyznaczenia wartości zapasu dla okresu planowanego można przyjąć następujący sposób kolejnego obliczania:

1) wartość średnia zapotrzebowania w okresach minionych to wartość prognozy dla okresu j = 1:

2) wartość prognozy dla okresu j = 2: V₂ = V₁ + a(Y₁ - V₁) = aY₁ + (1 - a)V₁

3) wartość prognozy dla okresu j = 3: V₃ = V₂ + a(Y₂ - V₂) = aY₂ + (1 - a)V₂ = aY₂ + a(1 - a)Y₁ + (1 - a)²V₁

4) wartość prognozy (planowany zapas) dla okresu w okresie k:

Z zależności tej wynika, że:

• wpływ na planowaną wielkość zapasu w okresie k poprzednich okresów jest tym mniejszy im bardziej są one odległe od okresu planowania;

• im większa jest wartość a (0 < a < 1), tym większy jest wpływ na prognozę zapotrzebowania danych z ostatnich okresów, jeżeli zaś a jest bliskie zera zwiększa się wpływ danych ze wszystkich okresów.

Jeżeli przyjąć założenie, że trend jest liniową funkcją czasu, to po wyznaczeniu jej postaci analitycznej, średnia wartość prognozy zapasu może być wyznaczona metodą ekstrapolacji.

Planowanie zapasów w wielopoziomowych systemach zaopatrywania

W wielopoziomowym systemie zaopatrywania wyróżniamy:

• magazyny szczebla podstawowego (j = 0), na którym odbywa się proces eksploatacji maszyn;

• magazyny szczebla wyższego, występujące na kolejnych szczeblach (j = 1, 2, ..., J) struktury hierarchicznej systemu zaopatrywania.

Zadaniem każdego magazynu szczebla podstawowego jest pokrycie z odpowiednim prawdopodobieństwem zapotrzebowania na części zamienne i materiały systemu eksploatacji, na rzecz którego pracuje. Określona liczba magazynów szczebla podstawowego jest podporządkowana (zgodnie ze strukturą organizacyjną terytorialną lub funkcjonalną) magazynowi szczebla wyższego. Zależność taka ma miejsce na każdym szczeblu struktury organizacyjnej systemu. Zadaniem magazynu szczebla nadrzędnego (na każdym poziomie) jest pokrycie ewentualnego niedoboru - różnicy między rzeczywistymi potrzebami a przewidywanym poziomem zapasu w magazynach szczebla niższego.

Rozpatrzymy proces planowania zapasów w magazynie j szczebla nadrzędnego względem poziomu podstawowego, na którym znajduje się i = 1, 2, ..., J podległych mu magazynów. Wielkość zapasów w każdym z magazynów szczebla podstawowego można wyznaczyć jedną ze znanych metod planowania zapasów. W danym magazynie szczebla podstawowego może wystąpić w planowanym okresie niedobór części wymiennych równy: X_i = Y_i - N_i

gdzie: - Y_i - możliwe rzeczywiste zapotrzebowanie na określony typ części;

- N_i - planowana wielkość zapasu w magazynie.

Wielkość niedoboru X_i jest zmienną losową, która może przyjmować wartości k = 0, 1, 2, 3,... z prawdopodobieństwami równymi:
(prawdopodobieństwo wystąpienia niedoboru o wartości k jest definiowane jako prawdopodobieństwo warunkowe tego, że wielkość rzeczywista zapotrzebowania Y_i będzie większa niż planowana wielkość zapasu N_i o k.

Prawdopodobieństwo P{Y_i > N_i} jest uzupełnieniem dystrybuanty rozkładu do jedności:

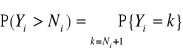
Wartość niedoboru części zamiennych w okresie planowania w danym magazynie szczebla podstawowego należy przewidywać na poziomie wartości oczekiwanej zmiennej losowej X_i, którą oznaczamy M_i:

Jeżeli niezawodność części zamiennej jest opisana rozkładem wykładniczym, to proces uszkodzeń jest prostym strumieniem Poissona o funkcji rozkładu prawdopodobieństwa

gdzie: λ - intensywność uszkodzeń danego typu części zamiennej;

l - planowana wartość zużycia miary eksploatacji przez maszyny w okresie planistycznym.

W tym przypadku wartość oczekiwana niedoboru w i - tym magazynie szczebla podstawowego jest równa:

gdzie F(N_i - 1) i F(N_i) są wartościami dystrybuanty rozkładu Poissona dla k = N_i - 1 oraz k = N_i i argumentu λl.

Sumaryczne zapotrzebowanie na brakujące elementy wszystkich magazynów szczebla podstawowego podporządkowanych magazynowi nadrzędnemu j jest równe :

Taka musiałaby być dodatkowa wielkość zapasu w magazynach szczebla podstawowego zabezpieczająca system eksploatacji przed możliwością powstania niedoboru części. Jeżeli zaś magazyny szczebla podstawowego mogą być zaopatrywane przez magazyn j szczebla nadrzędnego, to zgodnie z twierdzeniem o sumie wariancji, wielkość zapasu N_j w tym magazynie powinna być równa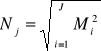

Zapas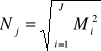
daje taki sam stopień zabezpieczenia ryzyka braku zapasu jak poziom zapasu dodatkowego
zgromadzonego w magazynach szczebla podstawowego.

Planowanie zapasu w magazynie szczebla nadrzędnego można także przeprowadzić na bazie zależności empirycznych. Załóżmy, że określony poziom zapasu w magazynach szczebla podstawowego jest równy N_i. Dla każdego magazynu przyjmujemy dodatkowy zapas αN_i, tzn. ze współczynnikiem bezpieczeństwa α. Stąd: M_i = αN_i, a wielkość zapasu w magazynie szczebla nadrzędnego: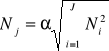

Jeżeli poziom zapasu w magazynach jest wyrażany za pomocą liczb całkowitych, to obliczane wielkości powinny być doprowadzone do liczb całkowitych jedną ze znanych metod zaokrąglania liczb (w dół, w górę, kombinowane).

W analogiczny sposób można wyznaczyć wielkości zapasów na wszystkich szczeblach struktury systemu zaopatrzenia rozpoczynając od poziomu podstawowego.

Przedstawione metody planowania zapasów wyczerpują w niewielkim stopniu wiedzę w tym zakresie. Wymienione jak i bardziej zaawansowane metody planowania są stosowane z szerokim wykorzystaniem komputerów. Szerokie zastosowanie znajdują wielokryterialne metody planowania, pozwalające na uwzględnianie wielu kryteriów efektywności gospodarowania zapasami takich jak:

• intensywność zużycia zapasu;

• koszt zaopatrywania;

• współczynnik gotowości zabezpieczanego parku maszyn;

• czas oczekiwania na dany asortyment;

• warunki eksploatacji maszyn;

• właściwości użytkowe części zamiennych;

• jakość eksploatacji maszyn.

Wprowadza się wówczas kryteria cząstkowe umożliwiające w określonym stopniu uwzględnienie wpływu na wielkość zapotrzebowania poszczególnych czynników.

Odrębną dziedzinę w zakresie planowania zapasów stanowią metody symulacji komputerowej. Umożliwiają przeanalizowanie większej ilości czynników charakteryzujących działanie systemu oraz rozpatrywanie wielu wariantów możliwych decyzji. Zastosowanie symulacji komputerowej wymaga dokładnej znajomości warunków działania systemu, umożliwiającej zbudowanie jego modelu matematycznego. Szczególne zastosowanie mają tutaj rezultaty badań niezawodności, pozwalające określić rozkłady prawdopodobieństwa uszkodzeń i zużycia części wymiennych i materiałów eksploatacyjnych. Istnieją pakiety oprogramowania służące do sterowania zapasami.

Przykład

Obliczyć wielkość optymalnej dostawy paliwa dla przedsiębiorstwa eksploatującego N = 100 pojazdów, jeżeli:

- przeciętna intensywność eksploatacji α_e pojedynczego pojazdu jest równa 50 km/dobę;

- przeciętne zużycie paliwa przez pojazd wynosi α_z = 40 l/100 km;

- pojazdy są użytkowane przeciętnie d = 20 dni w miesiącu;

- kwartalny koszt utrzymania zapasu paliwa wynosi średnio k_m = 2 zł/litr;

- koszt jednego zamówienia jest równy k_z = 1 500 zł;

- transport dokonywany jest za pomocą cystern o pojemności p_o = 5000 l.

Przy danych wartościach kosztów utrzymania zapasu i zamówień oraz danych pozwalających wyznaczyć całkowite zapotrzebowanie paliwa problem może być rozwiązany metodą Wilsona. Wyznaczymy wielkość zapotrzebowania w ciągu kwartału (dla tego okresu podana jest wartość kosztów utrzymania zapasu):

Q = 3 ⋅ α_e ⋅ α_z ⋅ N ⋅ d = 120 000 l

Wielkość optymalnej dostawy jest równa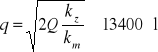
.

Liczba dostaw w ciągu kwartału byłaby równa
.

Ponieważ dostawy paliwa realizowane są za pomocą cystern o pojemności p, optymalna wielkość dostawy powinna stanowić wielokrotność pojemności środka transportowego. Wyznaczona wielkość dostawy q zawiera się w przedziale [2p = 10000 l, 3p = 15000 l]. Do wyznaczenia wielkości dostawy spełniającej warunek wielokrotności oraz minimum kosztów zaopatrywania rozważmy całkowity koszt zaopatrywania w modelu Wilsona dany wyrażeniem

Założona optymalna wielkość dostawy będzie równa 2p lub 3p (ponieważ K(q)) jest funkcją ciągłą i ma minimum w przedziale [2p,3p]. Podstawiając do powyższego wyrażenia obydwie wartości dostaw otrzymuje się odpowiednio wartości kosztu:

K(2p) = 28 000 zł

K(3p) = 27 000 zł

Optymalna wielkość dostawy powinna być równa 3p_o.

q

q

q

Z_min

Z

t_z1

t_z2

t_z3

t

t_d3

t_d2

t_d1

Z

t_z1

t_d1

t

q₄

q₃

q₂

q₁

T_c

Z_max

T_c

T_c

t_z2

t_z3

t_z4

t_d3

t_d2

C

B

A

C

B

A

udział

procentowy

asortymentu

a) b)

---