Ćwiczenie 7

TEMAT:

Wyznaczanie współczynnika lepkości dynamicznej cieczy.

Gęstość (masa właściwa) - jest wielkością służącą do porównywania ciężarów różnych materiałów, jako stosunek masy pewnej ilości substancji do zajmowanej przez nią objętości.

Wzór:

ρ =

Gdzie:

m - masa [kg]

V - objętość [m³]

Ciśnienie - wielkość skalarna określona jako wartość siły działającej prostopadle do powierzchni podzielona przez powierzchnię na jaką ona działa.

Wzór:

p =
[Pa]

Gdzie:

Fn - składowa siły prostopadła do powierzchni [N]

S - powierzchnia [m²]

Prędkość - jest wielkością informującą o tym jak szybko porusza się ciało.

Wzór:

V =

,

Gdzie:

ΔS - droga [m, km]

Δt - czas przebywania drogi S [s, h]

Przyspieszenie - jest wielkością informującą o tym jak szybko zmienia się

prędkość ciała.

Wzór:

a =
=

Gdzie:

V_p - prędkość początkowa

V_k - prędkość końcowa

Δt - czas, w jakim prędkość zmieniła się od V_p do V_k [s]

ΔV - różnica prędkości końcowej i początkowej

Ciśnienie hydrostatyczne - ciśnienie jakie wywiera na otaczające ciała ciecz nie będąca w ruchu

Wzór:

p = ρgh [Pa]

Gdzie:

ρ - gęstość cieczy

g - przyspieszenie ziemskie

h - głębokość zanurzenia w cieczy (od poziomu zerowego) [m]

Siła ciężkości - siła z jaką Ziemia lub inne ciało niebieskie przyciąga dane ciało. Ciężar jest wypadkową sił przyciągania grawitacyjnego i siły odśrodkowej wynikającej z ruchu obrotowego określonego ciała niebieskiego.

Wzór:

F = m * g [N]

Gdzie:

m - masa ciała [kg]

g - przyspieszenie ziemskie

Ruch laminarny cieczy - jest to przepływ uwarstwiony (cieczy lub gazu), w którym kolejne warstwy płynu nie ulegają mieszaniu. Ruch laminarny może odbywać się w cieczach o niskiej lepkości, takich jak woda, przy bardzo małych prędkościach. Przy ruchu laminarnym woda porusza się warstewkami (laminami) do siebie równoległymi, które się ze sobą nie krzyżują ani nie mieszają. Każda warstewka wody porusza się z prędkością większą niż przylegająca do niej warstewka niższa, ale mniejszą niż prędkość warstewki wyższej.

Lepkość (tarcie wewnętrzne) - cecha płynów, pojawienie się siły tarcia pomiędzy warstwami cieczy lub gazu, poruszającymi się równolegle względem siebie z różnymi co do wartości prędkościami. Warstwa poruszająca się szybciej działa przyspieszająco na warstwę poruszającą się wolniej i odwrotnie.

Zgodnie z laminarnym modelem przepływu, lepkość wynika ze zdolności płynu do przekazywania pędu pomiędzy warstwami poruszającymi się z różnymi prędkościami.

Wzór na współczynnik lepkości dynamicznej:

η =
[Pa * s]

Gdzie:

τ - naprężenie styczne [Pa]

γ - szybkość ścinania [s^-1]

Zasady dynamiki Newtona (prawa ruchu)

I Zasada Dynamiki Newtona (zasada bezwładności) - jeżeli na ciało nie działają żadne siły lub siły działające na ciało się równoważą to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.

II Zasada Dynamiki Newtona - jeżeli na ciało działają siły, które nie równoważą się (lub działa tylko jedna siła) to ciało porusza się ruchem przyśpieszonym, przy czym przyśpieszenie jakie posiada to ciało jest wprost proporcjonalne do siły wypadkowej działającej na ciało i odwrotnie proporcjonalne do masy ciała.

a =

Gdzie:

a - przyspieszenie

Fw - siła wypadkowa [N]

m - masa ciała [kg]

III Zasada Dynamiki Newtona (zwana zasadą akcji i reakcji) - jeżeli pierwsze ciało działa siłą na drugie ciało, to drugie ciało działa na pierwsze siłą o takiej samej wartości lecz przeciwnie skierowaną.

Prawo Archimedesa - na każde ciało zanurzone w płynie działa siła wyporu Fw skierowana pionowo do góry i co do wartości równa ciężarowi płynu (cieczy lub gazu) wypartego przez to ciało. Wartość tej siły jest równa:

Fw = ρgV [N]

Gdzie:

Fw - siła wyporu

ρ - gęstość

g - przyspieszenie ziemskie

V - objętość zanurzonego ciała [m^3­­­]

Prawo Stokesa - siła oporu F działająca na kulkę, poruszającą się w lepkim płynie jest wprost proporcjonalna do lepkości dynamicznej płynu η, promienia kulki r i do prędkości względnej kulki v. Wynika z tego następujący wzór:

F = 6π * η * r * V [N]

Gdzie:

η - lepkość dynamiczna cieczy [Pa * s]

r - promień kuli [m]

V - prędkość ciała względem cieczy

OBLICZENIA

Gęstość kulki:

ρ­₁ = 1,060 * 10³

Średnica kulki:

1. 2,13mm

2. 2,05mm

3. 2,16mm

4. 2,13mm

5. 2,10mm

	Kulka
Lp	2r [mm]	s1 [cm]	s­2 [cm]	l=s1-s2 [cm]	Τ [s]	2R [cm]
1		29,4	14,6	14,8	34,5
2					34,0
3					34,0
4					33,9
5					34,4
6					33,6

Lp	h1 [cm]	h2 [cm]	h3 [cm]	h1-h3 [cm]	h2-h3 [cm]	ρw[kg*m^-3]	t [ºC]	ρ2[kg*m^-3]
	47,7	56,1	23,7	24	32,4		24

Ćwiczenie 11

TEMAT:

Wyznaczanie równoważnika elektrochemicznego.

Rekombinacja - połączenie się dwóch różnoimiennych ładunków elektrycznych, proces odwrotny do jonizacji. Zjawisku rekombinacji jonu dodatniego i elektronu towarzyszy zazwyczaj wypromieniowanie nadwyżki energii elektronu w formie fotonu.

Przewodnictwo elektryczne w elektrolitach - związane jest z przepływem prądu, który jest związany z ruchem jonów. Powoduje to zmiany chemiczne i zmiany stężeń elektrolitów

przewodzących. Wraz ze wzrostem temperatury opór właściwy

elektrolitów na ogół maleje. Wielkość przewodności roztworów elektrolitów zależy od ich stężenia, temperatury, charakteru chemicznego substancji rozpuszczonej

(zdolności do dysocjacji na jony) i rodzaju rozpuszczalnika.

Elektroliza - ogół zjawisk występujących w warunkach przepływu prądu przez celę elektrolityczną (składającą się z naczynia zawierającego roztwór elektrolitu i

zanurzone w nim elektrody, podłączone do zewnętrznego obwodu. W obwodzie zewnętrznym znajduje się źródło prądu).

Do zjawisk tych należą:

• procesy transportu (wędrówka jonów do elektrod),

• procesy przejścia ładunku (między elektrodami, a składnikami roztworu: na elektrodzie ujemnej (katodzie) zachodzi redukcja kationów, na elektrodzie dodatniej (anodzie) - utlenianie anionów),

• reakcje chemiczne poprzedzające lub następujące po procesach przejścia ładunku.

Elektrolit - substancja, która po rozpuszczeniu w odpowiednim rozpuszczalniku, a niekiedy po stopieniu ulega dysocjacji jonowej i wskutek tego w stanie ciekłym lub w roztworach wodnych przewodzi prąd elektryczny dzięki obecności w niej swobodnie poruszających się jonów.

Dysocjacja elektrolityczna­ - jest to proces rozpadu cząsteczek kwasów, zasad i soli na jony swobodne pod wpływem wody. Dzięki temu procesowi w roztworach

wodnych powstają kationy i aniony, które stają się nośnikami prądu elektrycznego.

Pierwsze prawo elektrolizy Faradaya - masa m substancji wydzielonej na elektrodzie jest wprost proporcjonalna do natężenia prądu I płynącego przez elektrolit i do czasu t przepływu prądu, tj. do ładunku elektrycznego Q, który przepłynął przez elektrolit.

Wzór:

m = k * I * t = k * Q [g]

Gdzie:

k - równoważnik elektrochemiczny substancji

I - natężenie prądu elektrycznego [A]

t - czas przepływu prądu [s]

Q - ładunek elektryczny [C]

Drugie prawo elektrolizy Faradaya - stosunek mas m­­­₁ oraz m₂ substancji wydzielonych na elektrodach podczas przepływu jednakowych ładunków elektrycznych jest równy stosunkowi ich równoważników elektrochemicznych k₁ oraz k₂ i stosunkowi ich mas równoważnikowych R₁ oraz R₂.

Wzór:

Gdzie:

m - masa substancji [g]

k - równoważnik elektrochemiczny substancji

R - masa równoważnikowa substancji [g]

Stała Faradaya - stała fizyczna, która oznacza ładunek elektryczny przypadający na jeden mol elektronów. Stała Faradaya wynosi ok. 96 500 kulombów.

Wzór:

F = N_Ae

Gdzie:

N_A - stała Avogadra

e - ładunek elektronu [C]

Sens fizyczny stałej Faradaya - równoważniki elektrochemiczne różnych pierwiastków są wprost proporcjonalne do ich równoważników chemicznych. Innymi słowy, wydzielenie jednego gramorównoważnika jakiejkolwiek substancji wymaga zawsze tego samego ładunku elektrycznego.

Gęstość (masa właściwa) - jest to stosunek masy pewnej ilości substancji do zajmowanej przez nią objętości.

Wzór:

ρ =

Gdzie:

m - masa ciała [kg]

V - objętość ciała [m³]

Równanie Clapeyrona (równanie stanu gazu doskonałego) - to równanie stanu opisujące związek pomiędzy temperaturą, ciśnieniem i objętością gazu doskonałego, a w sposób przybliżony opisujący gazy rzeczywiste.

Wzór:

pV = nRT

Gdzie:

p - ciśnienie [Pa]

V - objętość [m³]

n - liczba moli gazu

T - temperatura (bezwzględna) [K]

R - uniwersalna stała gazowa:

R = N_Ak, gdzie: N_A - stała Avogadra, k - stała Boltzmanna, R = 8,314

Równanie to jest wyprowadzane na podstawie założeń:

• brak oddziaływań międzycząsteczkowych z wyjątkiem odpychania w momencie zderzeń cząsteczek

• objętość cząsteczek jest znikoma w stosunku do objętości gazu

• zderzenia cząsteczek są doskonale sprężyste

• cząsteczki znajdują się w ciągłym chaotycznym ruchu

Ciśnienie hydrostatyczne - ciśnienie jakie wywiera na otaczające ciała ciecz nie będąca w ruchu

Wzór:

p = ρgh [Pa]

Gdzie:

ρ - gęstość cieczy

g - przyspieszenie ziemskie

h - głębokość zanurzenia w cieczy (od poziomu zerowego) [m]

Ćwiczenie 12

TEMAT:

Pomiar oporu elektrycznego i wyznaczenie oporu właściwego metali.

Prawo Ohma - natężenie prądu elektrycznego płynącego przez przewodnik jest wprost proporcjonalne do wartości napięcia elektrycznego na jego końcach i odwrotnie proporcjonalne do rezystancji przewodnika.

Prawo Ohma wyraża się wzorem:

I =

Gdzie:

I - natężenie prądu elektrycznego [A]

U - napięcie elektryczne [V]

R - opór; rezystancja [Ω]

Po przekształceniu tego wzoru można uzyskać inne, równoważne wzory:

U = I*R

R =

Opór jest wielkością charakteryzująca dany element obwodu elektrycznego, określa jak dany element przeszkadza w przepływie prądu elektrycznego. Zależy więc od jego wymiarów, rodzaju przewodnika i warunków zewnętrznych np. temperatury, ciśnienia czy w niewielkim stopniu wilgotności.

Opór właściwy przewodnika - informuje nas o tym, jak duży jest opór tego przewodnika o długości 1 m i przekroju 1m². Najmniejszy opór właściwy mają przewodniki, a największy izolatory. Najlepszymi przewodnikami są metale.

Wzór na opór właściwy przewodnika:

R = ρ
[Ω * m]

Gdzie:

ρ - opór właściwy przewodnika [Ω * m]

l - długość przewodnika [m]

S - pole przekroju poprzecznego przewodu [m²]

W tabeli podano opory właściwe różnych ciał, wynika z niej, że opór właściwy różnych ciał zawiera się w bardzo szerokim przedziale.

Materiał	Rezystywność (Ω * m)
Srebro	1,59 * 10^-8
Miedź	1,70 * 10^-8
Złoto	2,44 * 10^-8
Aluminium	2,82 * 10^-8
Nikiel	6,99 * 10^-8
Żelazo	10 * 10^-8
Cyna	10,9 * 10^-8
Platyna	11 * 10^-8
Ołów	22 * 10^-8
Węgiel	3,5 * 10^-5
German	0,46
Krzem	640
Szkło	10^10 - 10^14
Guma	ok. 10^13
Siarka	10^15

^{Tabela rezystywności niektórych substancji (w temp. 20 °C)}

Prawa Kirchhoffa

Pierwsze prawo Kirchhoffa - suma natężeń prądów wpływających do węzła jest równa sumie natężeń prądów wypływających z tego węzła.

Pierwsze prawo Kirchhoffa można więc zapisać w postaci:

I₁ + I­­­­­­­­­­­­­­₂ + I_{3 ­}= I₄ + I₅

Drugie prawo Kirchhoffa - w dowolnym obwodzie zamkniętym suma sił elektromotorycznych jest równa sumie spadków napięć na elementach obwodu.

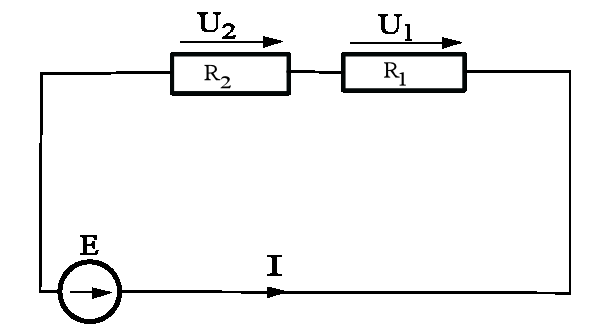
Wzór dla drugiego prawa Kirchoffa:

=

Gdzie:

ε_k - siła elektromotoryczna (SEM) k-tego źródła napięcia [V]

U_i - spadek napięcia na i-tym elemencie oczka [V]

OBLICZENIA

	Drut 1				Drut 2
Lp.	RN [Ω]	l1 [m]	l2 [m]	Rx [Ω]	RN [Ω]	l1 [m]	l2 [m]	Rx [Ω]
1	5,2	0,497	0,503	5,138	20,1	0,492	0,508	19,467
2	5,3	0,491	0,509	5,113	20,2	0,491	0,509	19,486
3	5,4	0,485	0,515	5,085	20,3	0,49	0,51	19,504
	= 5,112				= 19,486

= R_N *

	Drut 1		Drut 2
Lp	l [m]	d [mm]	l [m]	d [mm]
1	1,010	0,590	1,765	0,410
2	1,010	0,580	1,765	0,400
3	1,010	0,600	1,765	0,410
4	1,010	0,600	1,765	0,410
5	1,010	0,590	1,765	0,400
6	1,010	0,590	1,765	0,400
7	1,010	0,590	1,765	0,410
8	1,010	0,600	1,765	0,410
9	1,010	0,580	1,765	0,400
10	1,010	0,600	1,765	0,400
	= 1,010	= 0,592	= 1,765	= 0,405

ρ =
=

ρ₁ =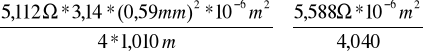

ρ₂ =

Ćwiczenie 16

TEMAT:

Wyznaczanie naprężeń za pomocą tensometru oporowego.

Prawo Hooke'a - zakładamy tu, że pewna siła odkształcająca (F) wywołuje odkształcenie Δl . W takim przypadku:

Odkształcenie jest wprost proporcjonalne do wywołującej je siły.

Wzór:

Δl =

Gdzie:

F - siła powodująca odkształcenie

l₀ - początkowa długość pręta [m]

S - pole przekroju poprzecznego [m]

E - moduł Younga (moduł sprężystości) - charakteryzuje twardość materiału

Prawo Ohma - natężenie prądu elektrycznego płynącego przez przewodnik jest wprost proporcjonalne do wartości napięcia elektrycznego na jego końcach i odwrotnie proporcjonalne do rezystancji przewodnika.

Prawo Ohma wyraża się wzorem:

I =

Gdzie:

I - natężenie prądu elektrycznego [A]

U - napięcie elektryczne [V]

R - opór; rezystancja [Ω]

OBLICZENIA

k = 2,15		E = 2,1*10
R = 0,20		R = 100,0
x = 59,7		L = 100cm
r [m]	x [cm]		Δx=x-x [cm]	δ
obciążenie własne belki	65,3		5,6	21,8
obciążenie z 1kg na ramię a1 = 20cm	67,5		7,8	30,4
a2 = 30cm	68,8		9,1	35,5
a3 = 40cm	69,9		10,2	39,8
a4 = 50cm	70,9		11,2	43,7
a5 = 60cm	71,9		12,2	47,6
a6 = 70cm	73,0		12,3	51,9
a7 = 80cm	73,9		14,2	55,4

Ćwiczenie 28

TEMAT:

Siatka dyfrakcyjna

Długość fali - najmniejsza odległość dwóch punktów będących w jednakowej fazie.

Zjawisko interferencji - polega na nakładaniu się pewnej liczby fal akustycznych, dając w ten sposób wzmocnienie lub osłabienie natężenia fali wypadkowej.

Zjawisko dyfrakcji - inaczej nazywana ugięciem fali, jest zjawiskiem polegającym na zmianie kierunku promieni fali na skutek pokonania przez falę przeszkody. Zjawiska dyfrakcji występują dla każdego typu ruchu falowego.

Siatka dyfrakcyjna - tworzy ją układ dużej liczby równych, równoległych i jednakowo rozmieszczonych szczelin oddzielonych nieprzeźroczystymi przerwami.

Stała siatki dyfrakcyjnej - to parametr charakteryzujący siatkę dyfrakcyjną. Wyraża on rozstaw szczelin siatki (odległość między środkami kolejnych szczelin).

Wzór na stałą siatki dyfrakcyjnej:

nλ = d * sinα

Gdzie:

n - rząd ugięcia (widma)

λ - długość fali

d - długość siatki

---