77 Fale świetlne i ich właściwości.

1.D)

2.E)

Jeżeli źródło umieści się w ogniskowej to da ono po odbiciu wiązkę równoległą.

R- promień Krzywizny,

R=2f , f- ogniskowa.

R=2⋅5=10cm

3.D)

Ognisko zwierciadła wklęsłego to punkty, w którym przecinają się odbite promienie równoległe. Ogniskowa zwierciadła to odległość ogniska od wierzchołka zwierciadła. Długość ogniskowej jest równa połowie promienia krzywizny zwierciadła.

4.E)

n₂<n₁

n₂<n₃>n₂<n₁i n₃

n₂sinβ=n₁sinα

n₂sinβ=n₃sinγ

n₁sinα=n₃sinγ

α>γ

sinα>sinγ

n₃=xn₁ x>1 n₂<n₁=n₃

5.C)

6.A)

r₁, r₂- prom. krzywizny

r₂=∝

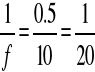
....f=20cm

7.C)

Z rysunków widać, że jeżeli będzie się zmniejszać przedmiot s do rozmiarów źródła światła, to wówczas jego obraz ciągle będzie powstawał na osi AB i będzie się zbliżał do punktu F₂-ogniskowej, oraz będzie malał do rozmiarów punktowych.

8.B)

D= -3+7=4 dioptrie

9.D)

p- powiększenie

l
f₁+f₂

ϕ₁-oko ogląda przedmiot pod tym samym kątem,

ϕ₂-widziany przedmiot przy pomocy lunety.

ϕ₁≅tgϕ₁

f₁=pf₂

f₁=16⋅4=64cm

10.B)

Jeżeli szerokość szczeliny d będzie w porównaniu równa λ długości fali świetlnej, wówczas nastąpi jej ugięcie po przejściu przez szczelinę. Ugięcie nastąpi w kierunku prostopadłym do szczeliny.

-linie przerywane - pozorny bieg promieni, jaki wydaje się obserwatorowi.

11.E)

730nm- odpowiada barwie czerwonej światła w próżni.

12.A)

Prawo Brewstera:

Jeżeli światło pada na granicę dwóch ośrodków tak, że promień odbity jest prostopadły do promienia załamanego, to promień odbity jest całkowicie spolaryzowany.

β#α, α+β=90^o

78 Fale świetlne i ich właściwości.

1.E)

R=1m, I=2cd,

φ=IΩ=8Π

2.D)

Z prawa Lamberta:

E₁=9E₂

3.B)

p<1 pozorny odwrócony

wiązka światła padając na zwierciadło kuliste wyp. Ulega rozproszeniu, więc obraz powstanie po drugiej stronie zwierciadła (należy przedłużyć promienie odbite), obraz zawsze jest pozorny: p<1

4.D)

Przy wyjściu szkło-powietrze, promień 3 powinien się załamać.

5.E)

η_s=1.5, η_w=1.33

6.D)

α₁-kąt padania,

α₂-kąt wyjścia,

E- kąt łamiący,

δ-odchylenie.

δ=α₁+α₂-E

Najmniejsze odchylenie zachodzi wówczas, gdy α₁=α₂ symetryczne przejście światła przez pryzmat.

7.D)

Mówi samo za siebie.

8.C)

9.A)

A''B-obraz w mikroskopie

p>1

urojony (przedłużenie promieni)

odwrócony (w stosunku do przedmiotu)

10.A)

Doświadczenie Younga -polegało na przepuszczeniu światła przez dwie szczeliny. Jedynie fale spójne mogą interferować i tworzyć obraz interferencyjny. Fale będą spójne, jeśli będą posiadać stałą w czasie, różnicę faz wynikającą z różnicy dróg.

11.A)

fioletowa- 0.40-0.45μm

niebieska- 0.45-0.49

zielona- o.49-o.56

żółta- 0.56-0.58

pomarańczowa-0.58-0.61

czerwona- 0.61-0.70

ad pytanie- odległość od prążka zerowego zależy od długości fali (dł. Koloru fali)0, im długość krótsza , odległość mniejsza.

12.B)

ϕ=kcl

ϕ-kąt skręcenia polaryzacji,

k- współczynnik (zależy od rodzaju substancji i st. procent. i od dł. fali)

c- st. procentowy,

l- dł. roztworu.

α=kc₁l₁

4α=kc_xl₂ 4kc₁l₁=kc_xl₂

81 Fotony, emisja i absorpcja promieniowania.

1.E)

E=hν,

,

dla λ małego - E -duże

λ najmniejszą mają promienie fioletowe.

2.A)

E=hν

E=6.62⋅10^-34⋅10¹⁴J⋅s⋅

E=6.62⋅10^-20J

Foton przekaże całą swoją energię E elektronowi.

3.A)

Jeżeli v jest dostatecznie duże, prąd fotoelektryczny osiąga pewną graniczną wartość. Jeżeli zmienimy znak v natężenie prądu fotoelektrycznego nie spadnie gwałtownie do zera. Dowodzi to, ze z płytki A emitowane są elektrony o prędkościach różnych od zera. Niektóre w nich , dochodzą do naczynia B, pomimo faktu, że pole elektryczne przeciwdziała ich ruchowi. Jeżeli odwróconą różnicę potencjałów dostatecznie zwiększymy, to osiągniemy taką wartość v₀, przy której natężenie prądu fotoelektrycznego spada do zera.

4.C)

, n=1,2,3, n- nr.powłoki

5.C)

Elektron może przejść z powłoki k na n k>n oddając energię E_k-E_n, albo z n na k n<k dostając energię E_k-E_n

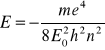
Albo:

, R-stała Rydeberga

2→1 4→2 6→3

,

E₁= - hcR,

ΔE>ΔE'>ΔE''

6.E)

7.A)

8.D)

Linie Fraunhofera:

Jest to różnica wsp. załamania η_F-η_C długości światła fioletowego i czerwonego.

LF są miarą dyspersji światła. LF w widmie Słońca są odwróceniem widm emisyjnych pierwiastków gazowych znajdujących się w zewn. warstwach Słońca, tak więc są one widmem absorpcyjnym Słońca.

9.C)

Rozgrzane do wysokiej temp. ciała stałe oraz ciecze, wysyłają one nie poszczególne linie, ale jasne nieprzerywalne pasmo, w którym poszczególne barwy płynnie przechodzą w siebie (przykład zmiana barwy ciał stałych - metali podczas ogrzewania T- wysokie.)

10.C)

Dł. fali czerwonej - 0.61-0.70 [ν_c 4.9⋅10¹⁴-4.3⋅10¹⁴]

Dł. Fali zielonej -0.49-0.56 [ν_z 6.10¹⁴-5.4⋅10¹⁴]

W wyniku nałożenia się fali czerwonej i zielonej powstanie fala żółta (mieszanie barw).

11.D)

Przedmiot pokryty idealnym zielonym barwnikiem będzie pochłaniał fale innego koloru, a odbijał koloru zielonego. Jeżeli zostanie oświetlony światłem koloru czerwonego (jednorodnym) wówczas dokona on absorpcji tego światła nie odbijając żadnego, dlatego jego kolor będzie wydawał się być czarnym.

12.A)

W miarę wzrostu temp. bezwzględnej ciała doskonale czarnego coraz większe ilości wypromieniowanej energii odpowiada falom krótkim. Prawo Wiena.

Ciało doskonale czarne.

Iloczyn długości fali λ_max odpowiadający największemu natężeniu i jego temp. bezwzgl. T ma wartość stałą.

λ_maxT=2897(=C) μmK

Jeżeli T rośnie, λ- maleje.

82 Fotony, emisja i absorpcja promieniowania.

1.C)

p=mv

E=mc²

E=hγ

p_⊥=

2.D)

W=4.8⋅10^-19J

pr. Einsteina-Millikana

dla najwolniejszych v→0

hγ=w

,

λ=0.4⋅10^-6m

3.E)

Dla fotokom. próżniowej:

r₁=1m

I₁=10mA

r₂=2m φ₁=E₁S

φ₂=E₂S

φ₁=IS

φ₂⇒φ₁-zależność liniowa, wobec tego I₂=2.5 mA

4.C)

γ-częstotliwość

5.D)

_p>n

Dla serii Paschena n=3 , aby energia prążka minimalna (E=hγ), to γ musi być minimalne

n=3

γ_minimalne dla

czyli dla p=4 n=3

6.B)

k=2,3,4... n=1

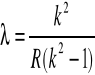
dla k=2 R=1.097⋅10⁷

λ=122 nm nadfiolet

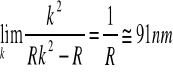
promienie Roentgena λ_górna

7.B)

SERIE: Elektrony przeskakują na orbitę n=... z orbit wyższych

Lymana n=1 bliskie nadfioletu

Balmera n=2 4y pierwsze
-światło widzialne, reszta bliskie nadfioletu

Paschena n=3

Bracketta n=4 bliskie podczerwieni.

8.C)

Pochłaniane są te długości fal, które dane źródło emituje świecąc. Stąd po przejściu światła żółtego przez pary jakiegoś pierwiastka nie daje już widma odpowiedniego, tylko brakuje tej długości fali jaka jest emitowana.

9.E)

Natężenie promieniowania E_C ciała doskonale czarnego jest wprost proporcjonalna do czwartej potęgi jego temperatury bezwzględnej.

E_C=δT⁴ δ-stała Stefana Boltzmana

Stosunek natężenia E promieniowania wysyłanego przez dowolne ciało do natężenia E_c promieniowania ciała doskonale czarnego (w tej samej temp. bezwzgl.T) jest równe współczynnikowi pochłaniania „a” tego ciała :

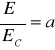
(c.d.c. a=1)

Im większa zdolność absorpcyjna tym większa zdolność emisyjna.

10.E)

Filtry-pochłaniane barwy i odbijane.

11.D)

Biały kolor odbije falę niebieską i przyjmie ten kolor, natomiast kolor czerwony pochłonie i będzie czarny.

12.E)

Widmo pierw. pozwala określić i zidentyfikować jakie atomy wysyłają promieniowanie. Należy znać dł. fal poszczególnych linii, którą można określić z położenia poszczególnych linii znając krzywą dyspersji.

---