Poz. 1 Dach

Dane:

• Nachylenie połaci dachowej: α = 45°,

• Konstrukcja dachu: płatwiowo - kleszczowa, drewno sosnowe,

• Maksymalny rozstaw krokwi: a_max=1,00m. (średnio 0,80 m. ) ,

• Pokrycie: blacha trapezowa gr. 0,75 mm, wysokości 55mm,

• Obciążenie śniegiem: strefa 4,

• Obciążenie wiatrem: strefa 3,

• Położenie budynku: 350m. n.p.m.

Poz. 1.1 Podkład pod pokrycie - łata

1. Zestaw obciążeń

Przyjęto:

• Rozstaw łat co 0,5 m

• Łaty o wymiarach 45⋅63 mm => A = 2,835⋅10^-3 m², ρ_sosny = 5,5 kN/m³

# Obciążenia stałe

Tabela 1.1.Zestawienie obciążeń stałych

Obciążenia	Wartość Charakterystyczna [kN/m]	Współczynnik obciążenia γf	Wartość Obliczeniowa [kN/m]
Ciężar własny łaty 0,002835⋅5,5 Ciężar dachówki: 0,091⋅0,5	0,016 0,046	1,1 1,2	0,018 0,055
Razem :	0,062		0,073

# Obciążenie skupione (człowiek z narzędziami)

P_k = 1,0 kN, γ_f = 1,2 => P_d = 1,0⋅1,2 = 1,2 kN.

#Obciążenie zmienne

Obciążenie charakterystyczne śniegiem S _na na 1 m² powierzchni rzutu dla 4 strefy (wg PN- 80/B-02010):

S_k = Q_k⋅ C

gdzie:

Q_k = 0,003 H ≥ 0,9 kN/m², w tym: H - wysokość w m. n.p.m.

Q_k = 0,003 ⋅ 350 = 1,05 kN/m.

C₁ = 0,8⋅ [ (60 - α) / 30 ] = 0,8⋅ [(60 - 45)/30] = 0,4

C₂ = 1,2⋅[ (60 - α) / 30] = 1,2⋅[ (60 -45) / 30] = 0,6

S_k = 1,05⋅ 0,4 = 0,42

Obciążenie charakterystyczne wywołane działaniem wiatru (wg PN-77/B-02011) dla 3 strefy:

p_k = q_k⋅ C_e⋅ C⋅ β

gdzie:

q_k = 250 + 0,5 ⋅ H ≥ 350

q_k = 250 + 0,5⋅ 350 = 425 Pa => q_k = 0,425kN/m

C_e = 0,8

C = Cz = 0,015α - 0,2 = 0,475 - połać nawietrzna

C_z = -0,4 - połać zawirtrzna

β = 1,8

Tabela 1.2. Zestawienie obciążeń zmiennych

Obciążenie	Wartość charakterystyczna [kN/m]	Współczynnik obciążenia γf	Współczynnik jednoczesności Obciążeń Zmiennych ψ°	Wartość obliczeniowa [kN/m]
Śnieg Sk⋅0,5 m = 1,05⋅0,4⋅0,5 Wiatr pk⋅0,5 m = 0,425⋅0,8⋅0,475⋅1,8⋅0,5	0,21 0,14535	1,4 1,3	0,9	0,294 0,17

1. Schemat statyczny I - ciężar własny + człowiek

Przyjęłam średni rozstaw miedzy krokwiami lśr = 0,80 m.

Składowe obciążenia charakterystycznego:

P_k⊥ = P_k⋅cosα = 0,7071⋅ P_k

P_k = P_k sinα = 0,7071⋅P_k

g_k⊥ = g_k⋅cosα = 0,7071⋅ g_k

g_k = g_k⋅sinα = 0,7071 g

#Sprawdzenie stanu granicznego nośności (zginanie)

• Wykres momentów zginających dla składowych prostopadłych obciążenia

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Obciążenie skupione" Zmienne 1 1,00 1,20

C -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

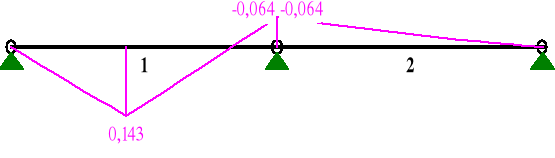
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABC

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 0,423 0,000

0,43 0,346 0,143* -0,443 0,000

0,43 0,346 0,143* 0,405 0,000

1,00 0,800 -0,064 -0,467 0,000

2 0,00 0,000 -0,064 0,100 0,000

1,00 0,800 0,000 0,059 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

• Wykres momentów zginających dla składowych równoległych obciążenia

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Obciążenie skupione" Zmienne 1 1,00 1,20

C -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

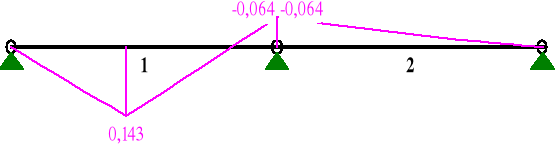
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABC

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 0,423 0,000

0,43 0,346 0,143* -0,443 0,000

0,43 0,346 0,143* 0,405 0,000

1,00 0,800 -0,064 -0,467 0,000

2 0,00 0,000 -0,064 0,100 0,000

1,00 0,800 0,000 0,059 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

• Sprawdzenie wyników:

k_m ( σ_m,y,d / f_m,y,d ) + σ_m,z,d / f_m,z,d ≤ 1,

lub

σ_m,y,d / f_m,y,d + k_m ( σ_m,z,d / f_m,z,d) ≤ 1,

gdzie:σ_m,y,d i σ_m,z,d - naprężenia obliczeniowe od zginania w stosunku do osi głównych,

f_m,y,d i f_m.,z,d - odpowiadające tym naprężeniom wytrzymałości obliczeniowe na zginanie,

k_m = 0,7 - dla przekrojów prostokątnych,

σ _m,y,d = M_y / W_y, σ_m,z,d = M_z / W_z gdzie:

W_y, W_z - wskaźniki wytrzymałości.

Wy = 0,045⋅ 0,063² / 6 = 29,77⋅10^-6 m³, W_z = 0,063⋅0,045² / 6 = 21,26⋅10^-6 m³.

σ _m,y,d = 0,143 / 29,77⋅10^-6 = 4803,49 KPa = 4,80349 MPa

σ_m,z,d = 0,143 / 21,26⋅10^-6 = 6726,2465 KPa = 6,7265 MPa

f_m,y,d = k_mod ⋅ f_m,y,k / γ_M ,

gdzie:

f_m,y,k - wytrzymałość charakterystyczna na zginanie. Dla klasy drewna C30 f_m,y,k = 30 MPa,

γ_M. = 1,3 - częściowy współczynnik bezpieczeństwa,

k_mod = 1,1 - współczynnik kodyfikujący dla klas użytkowania i czasu trwania obciążenia (człowiek z narzędziami - obciążenie chwilowe),

f_m,y,d = f _m,z,d = 1,1⋅ 30,0 / 1,3 = 25,38 MPa.

k_m⋅( σ _m,y,d /f_m,y,d ) + σ_m,z,d / f _m,z,d = 0,7⋅ ( 4,80349 / 25,38 ) + 6,7265 / 25,38 = 0,3975 < 1,

lub

σ _m,y,d / f_m,y,d + k_m⋅(σ_m,z,d / f _m,z,d ) = 4,80349 / 25,38 + 0,7⋅ ( 6,7265 / 25,38 ) = 0,3748 < 1.

W odniesieniu do powyższego schematu, warunek stanu granicznego nośności został spełniony.

# Sprawdzenie stanu granicznego użytkowalności

u _net.fin = L / 150 = 800 / 150 = 5,3(3) mm.

Wariant I (obliczenia dokładne)

Po wykonaniu obliczeń w programie RM-Win dla obciążeń charakterystycznych otrzymano następujące wartości ugięcia:

Wykresy ugięcia dla składowych prostopadłych obciążenia

• Od obciążenia siłą skupioną (obciążenia krótkotrwałe):

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

B -"Obciążenie skupione" Zmienne 1 1,00 1,20

------------------------------------------------------------------

PRZEMIESZCZENIA:

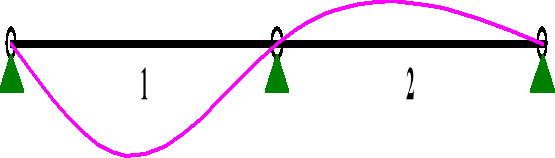
DEFORMACJE: T.I rzędu

Obciążenia char.: B

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,114 0,067 0,0005 1665,9

2 -0,0000 0,0000 0,067 -0,034 0,0002 4416,6

------------------------------------------------------------------

u_inst1,y = 0,0005 m = 0,5 mm,

k_def = 0 ( obciążenie krótkotrwałe),

u_fin1,y = u _inst1,y ⋅ (1 + k_def ) = 0,50 mm.

• Od obciążenia ciężarem własnym (obciążenie stałe)

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

C -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

PRZEMIESZCZENIA:

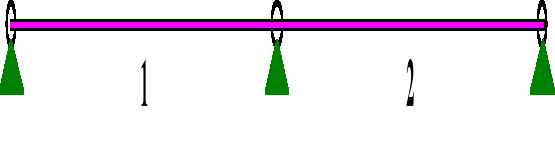
DEFORMACJE: T.I rzędu

Obciążenia char.: AC

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 0,0000 -0,002 0,000 0,0000 92791,2

2 -0,0000 0,0000 0,000 0,002 0,0000 92791,2

-----------------------------------------------------------------

u_inst2,y = 0 mm

k_def = 0,8 ( klasa trwania obciążenia = stałe, klasa użytkowania = 2 )

u_fin2,y = u_fin2,y ( 1 + k_def ) = 0 mm.

Ugięcie sumaryczne:

u_fin,y = u_fin1,y + u_fin2,y = 0,5 + 0 = 0,5 mm,

Wykresy ugięcia dla składowych równoległych obciążenia

• Od obciążenia siłą skupioną (obciążenia krótkotrwałe):

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

B -"Obciążenie skupione" Zmienne 1 1,00 1,20

------------------------------------------------------------------

PRZEMIESZCZENIA:

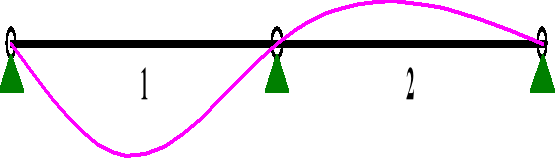
DEFORMACJE: T.I rzędu

Obciążenia char.: B

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,114 0,067 0,0005 1665,9

2 -0,0000 0,0000 0,067 -0,034 0,0002 4416,6

------------------------------------------------------------------

u_inst1,z = 0,0005 m = 0,5 mm,

k_def = 0 ( obciążenie krótkotrwałe),

u_fin1,z = u _inst1,y ⋅ (1 + k_def ) = 0,50 mm.

• Od obciążenia ciężarem własnym (obciążenie stałe)

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

C -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

PRZEMIESZCZENIA:

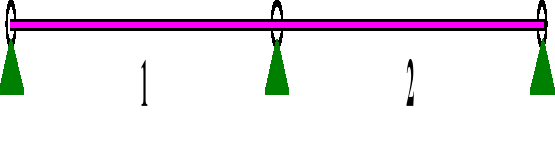
DEFORMACJE: T.I rzędu

Obciążenia char.: AC

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 0,0000 -0,002 0,000 0,0000 92791,2

2 -0,0000 0,0000 0,000 0,002 0,0000 92791,2

------------------------------------------------------------------

u_inst2,z = 0 mm

k_def = 0,8 ( klasa trwania obciążenia = stałe, klasa użytkowania = 2 )

u_fin2,z = u_fin2,y ( 1 + k_def ) = 0 mm.

Ugięcie sumaryczne:

u_fin,z = u_fin1,z + u_fin2,z= 0,5 + 0 = 0,5 mm,

Ugięcie całkowite:

u _fin = 0,71mm < u _net.fin = 5,3(3)mm

Stan graniczny użytkowalnośći został spełniony.

1. Schemat statyczny II - ciężar własny + śnieg + wiatr

Składowe obciążenia charakterystycznego:

g_k⊥ = g_k ⋅ cosα = 0,707⋅g_k,

g _k|| = g_k ⋅sinα = 0,707⋅g_k,

S_k⊥ = S_k ⋅cos²α = 0,707²⋅S_k = 0,5⋅S_k,

S_k|| = S_k ⋅sinα⋅cosα = 0,7071² S_k = 0,5⋅S_k,

p_k⊥ = p_k⋅ ψ_° = p_k⋅ 0,9*,

p_k|| = 0

*Uwzględniam współczynnik jednoczesności obciążeń ψ_° =0,9 ( wg PN-82/B-02000)

# Sprawdzenie stanu granicznego nośności (zginanie)

• Wykres momentów zginających dla składowych prostopadłych obciążenia

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Śnieg" Zmienne 1 1,00 1,40

C -"Wiatr" Zmienne 1 1,00 1,30

D -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

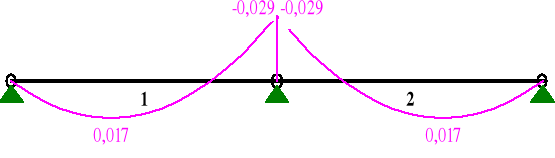
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABCD

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 0,111 0,000

0,38 0,306 0,017* -0,002 0,000

0,37 0,297 0,017* 0,001 0,000

1,00 0,800 -0,029 -0,184 0,000

2 0,00 0,000 -0,029 0,184 0,000

0,63 0,506 0,017* -0,002 0,000

0,62 0,497 0,017* 0,001 0,000

1,00 0,800 0,000 -0,111 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

• Wykres momentów dla składowych równoległych obciążenia

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"Ciężar własny łaty" Stałe 1,10

B -"Śnieg" Zmienne 1 1,00 1,40

D -"Ciężar własny blachy trap." Stałe 1,20

------------------------------------------------------------------

MOMENTY:

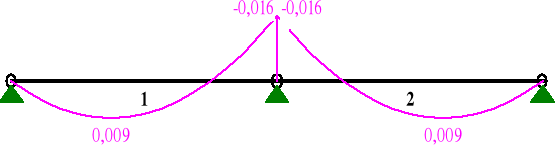
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABD

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 0,060 0,000

0,39 0,313 0,009* -0,002 0,000

0,36 0,291 0,009* 0,002 0,000

1,00 0,800 -0,016 -0,099 0,000

2 0,00 0,000 -0,016 0,099 0,000

0,64 0,513 0,009* -0,002 0,000

0,61 0,491 0,009* 0,002 0,000

1,00 0,800 0,000 -0,060 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

Wniosek:

Jak widać otrzymane wartości momentów zginających, zarówno w przypadku obciążeń działających prostopadle jak i równolegle do połaci dachowej są mniejsze od wartości otrzymanych w schemacie I ( ciężar własny + człowiek). Wynika z tego, że ta kombinacja obciążeń jest mniej niebezpieczna dla sprawdzanego ustroju i dlatego nie ma potrzeby sprawdzania stanu granicznego nośności oraz stanu granicznego użytkowalności.

Poz 1.2 Wiązar płatwiowo - kleszczowy

Przyjęto wstępnie:

krokwie 8,0 × 16,0 cm

kleszcze 2× 5,0 × 14,0 cm

1.2.1 Zestawienie obciążeń

Zestawienie obciążeń połaci dachowych przedstawiłam w tabeli 1.3. Składowe obciążenia połaci obliczono, korzystając z zależności:

g_k⊥ = g_k ⋅ cosα = 0,707⋅g_k,

g _k|| = g_k ⋅sinα = 0,707⋅g_k,

S_k⊥ = S_k ⋅cos²α = 0,707²⋅S_k = 0,5 ⋅ S_k,

S_k|| = S_k ⋅sinα⋅cosα = 0,707² S_k = 0,5 ⋅ S_k,

p_k⊥ = p_k⋅ ψ_° = p_k ⋅ 0,9*,

p_k|| = 0

P_k⊥ = P_k ⋅ cosα = 0,707 ⋅ P_k

P_k|| = P_k ⋅ sinα = 0,707 ⋅ P_k

Tabela 1.3 zestawienie obciążeń połaci dachowych więżby płatwiowo - kleszczowej

Obciążenie	Wartość charaktery- styczna [kN/m]	Współ- czynnik obcią- żenia γF	Wartość Obliczenio-wa [kN/m]	Składowe prostopadłe obciążenia		Składowe równoległe obciążenia
								wartość charaktery- styczna [kN/m]	wartość obliczenio-wa [kN/m]	wartość charaktery- styczna [kN/m]	wartość obliczeniowa [kN/m.]
Ciężar własny pokrycia z uwzględnieniem ciężaru krokwi ciężar łaty 0,016 ⋅ 2⋅ 0,8 m. ciężar własny blachy trapezowej 0,091 ⋅ 0,8 m ciężar własny krokwi 0,08⋅0,160⋅ 5,5 ciężar własny wełny mineralnej 0,15⋅2,0⋅0,8 ciężar własny płyty gipsowo-kartonowej 0,019⋅12,0⋅0,8 RAZEM: Śnieg połać lewa Sk = Qk ⋅ C2 = 1,05 ⋅ 0,6 ⋅ 0,8 połać prawa Sk = Qk ⋅ C1 = 1,05 ⋅ 0,4 ⋅ 0,8 Wiatr połać nawietrzna pk1 = qk ⋅ Ce ⋅C ⋅ β = = 0,425⋅ 0,8⋅ 0,475⋅1,8 połać zawietrzna pk2 = qk ⋅ Ce ⋅C ⋅ β = = 0,425⋅ 0,8⋅ 0,225⋅ 1,8 Ciężar własny kleszczy 2 ⋅ 0,05 ⋅ 0,14 ⋅ 5.5	0,0256 0,0728 0,0704 0,24 0,182 gk = 0,591 Sk = 0,504* Sk = 0,336* pk1=0,2907 pk2= -0,245 gk2 =0,077	1,1 1,2 1,1 1,2 1,2 1,4 1,4 1,3 1,3 1,1	0,0282 0,0874 0,0774 0,288 0,219 gd=0,7 Sd=0,706* Sd=0,470* pd1=0,3779 pd2=-0,318 gd2=0,0847	0,0181 0,0515 0,0498 0,170 0,129 gk⊥=0,418 Sk⊥=0,252 Sk⊥=0,168 pk⊥1=0,262** pk⊥2= -0,286** -	0,0199 0,0618 0,0547 0,204 0,155 gd⊥=0,495 Sd⊥=0,353 Sd⊥=0,235 pd⊥1=0,34** pd⊥2=-0,372** -	0,0181 0,0515 0,0498 0,170 0,129 gk||=0,418 Sk||=0,252 Sk||=0,168 - - -	0,0199 0,0618 0,0547 0,0199 0,155 gd||=0,495 Sd||=0,353 Sd||=0,235 - - -
Obciążenie skupione ( człowiek obciążający kleszcze)	Pk = 1,00 [kN]	1,2	Pd= 1,20 [kN]	-	_	_	_

* Wartość na 1 m² powierzchni rzutu dachu

** Uwzględniono współczynnik jednoczesności obciążeń ψ_° = 0,9

1.2.2 Schemat statyczny

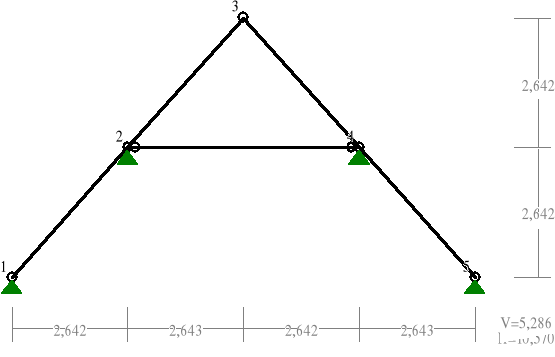
1.2.3 Wyznaczenie sił wewnętrznych

Obliczenia wykonałam przy użyciu programu RM-Win.

WĘZŁY:

------------------------------------------------------------------

Nr: X [m]: Y [m]: Nr: X [m]: Y [m]:

------------------------------------------------------------------

1 0,000 0,000 4 7,927 2,644

2 2,642 2,643 5 10,570 0,001

3 5,285 5,286

PODPORY: P o d a t n o ś c i

------------------------------------------------------------------

Węzeł: Rodzaj: Kąt: Dx(Do*): Dy: DFi:

[ m / k N ] [rad/kNm]

------------------------------------------------------------------

1 stała 0,0 0,000E+00 0,000E+00

2 przesuwna 0,0 0,000E+00*

4 przesuwna 0,0 0,000E+00*

5 przesuwna 0,0 0,000E+00*

OSIADANIA:

------------------------------------------------------------------

Węzeł: Kąt: Wx(Wo*)[m]: Wy[m]: FIo[grad]:

------------------------------------------------------------------

B r a k O s i a d a ń

PRĘTY:

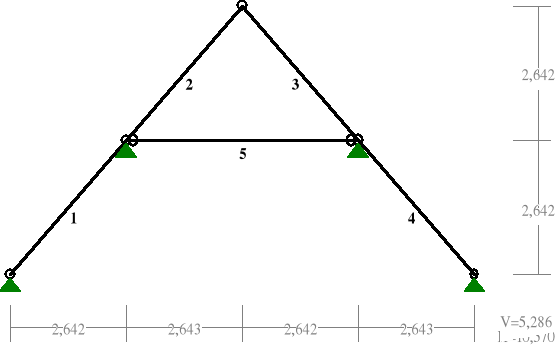
PRZEKROJE PRĘTÓW:

PRĘTY UKŁADU:

Typy prętów: 00 - sztyw.-sztyw.; 01 - sztyw.-przegub;

10 - przegub-sztyw.; 11 - przegub-przegub

22 - cięgno

------------------------------------------------------------------

Pręt: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ: Przekrój:

------------------------------------------------------------------

1 00 1 2 2,642 2,643 3,737 1,000 3 Krokiew 160x80

2 01 2 3 2,643 2,643 3,738 1,000 3 Krokiew 160x80

3 10 3 4 2,642 -2,642 3,736 1,000 3 Krokiew 160x80

4 00 4 5 2,643 -2,643 3,738 1,000 3 Krokiew 160x80

5 11 2 4 5,285 0,001 5,285 1,000 1 Kleszcze 2×50x140

------------------------------------------------------------------

WIELKOŚCI PRZEKROJOWE:

------------------------------------------------------------------

Nr. A[cm2] Ix[cm4] Iy[cm4] Wg[cm3] Wd[cm3] h[cm] Materiał:

------------------------------------------------------------------

1 140,0 2287 1167 327 327 14,0 25 Drewno C30

3 128,0 2731 683 341 341 16,0 25 Drewno C30

------------------------------------------------------------------

STAŁE MATERIAŁOWE:

------------------------------------------------------------------

Materiał: Moduł E: Napręż.gr.: AlfaT:

[N/mm2] [N/mm2] [1/K]

------------------------------------------------------------------

25 Drewno c30 12000 18,000 0,00E+00

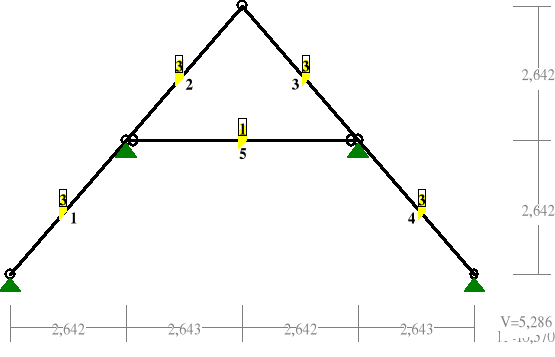
OBCIĄŻENIA:

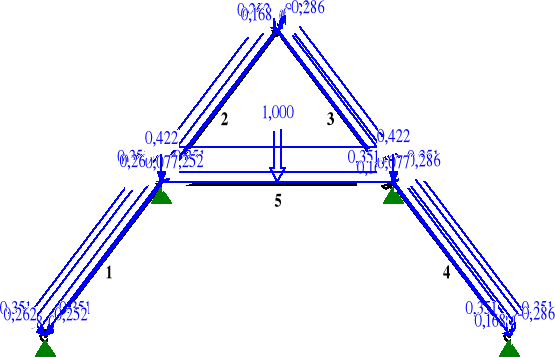
OBCIĄŻENIA: ([kN],[kNm],[kN/m])

------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------

Grupa: A "C.wł. łata+krok,kleszcze" Stałe γf= 1,10

1 Liniowe 45,0 0,068 0,068 0,00 3,74

1 Liniowe -45,0 0,068 0,068 0,00 3,74

2 Liniowe 45,0 0,068 0,068 0,00 3,74

2 Liniowe -45,0 0,068 0,068 0,00 3,74

3 Liniowe -45,0 0,068 0,068 0,00 3,74

3 Liniowe 45,0 0,068 0,068 0,00 3,74

4 Liniowe -45,0 0,068 0,068 0,00 3,74

4 Liniowe 45,0 0,068 0,068 0,00 3,74

5 Liniowe 0,0 0,077 0,077 0,00 5,29

Grupa: B "Śnieg" Zmienne γf= 1,40

1 Liniowe 45,0 0,252 0,252 0,00 3,74

1 Liniowe -45,0 0,252 0,252 0,00 3,74

2 Liniowe 45,0 0,252 0,252 0,00 3,74

2 Liniowe -45,0 0,252 0,252 0,00 3,74

3 Liniowe -45,0 0,168 0,168 0,00 3,74

3 Liniowe 45,0 0,168 0,168 0,00 3,74

4 Liniowe -45,0 0,168 0,168 0,00 3,74

4 Liniowe 45,0 0,168 0,168 0,00 3,74

Grupa: C "Wiatr" Zmienne γf= 1,30

1 Liniowe 45,0 0,262 0,262 0,00 3,74

2 Liniowe 45,0 0,262 0,262 0,00 3,74

3 Liniowe -45,0 -0,286 -0,286 0,00 3,74

4 Liniowe -45,0 -0,286 -0,286 0,00 3,74

Grupa: D "Człowiek" Zmienne γf= 1,20

5 Skupione 0,0 1,000 2,64

Grupa: E "Ciężar własny pokrycia" Stałe γf= 1,20

1 Liniowe 45,0 0,351 0,351 0,00 3,74

1 Liniowe -45,0 0,351 0,351 0,00 3,74

2 Liniowe 45,0 0,051 0,051 0,00 3,74

2 Liniowe -45,0 0,051 0,051 0,00 3,74

3 Liniowe -45,0 0,051 0,051 0,00 3,74

3 Liniowe 45,0 0,051 0,051 0,00 3,74

4 Liniowe -45,0 0,351 0,351 0,00 3,74

4 Liniowe 45,0 0,351 0,351 0,00 3,74

5 Liniowe 0,0 0,422 0,422 0,00 5,29

------------------------------------------------------------------

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"C.wł. łata+krok,kleszcze" Stałe 1,10

B -"Śnieg" Zmienne 1 1,00 1,40

C -"Wiatr" Zmienne 1 1,00 1,30

D -"Człowiek" Zmienne 1 1,00 1,20

E -"Ciężar własny pokrycia" Stałe 1,20

MOMENTY:

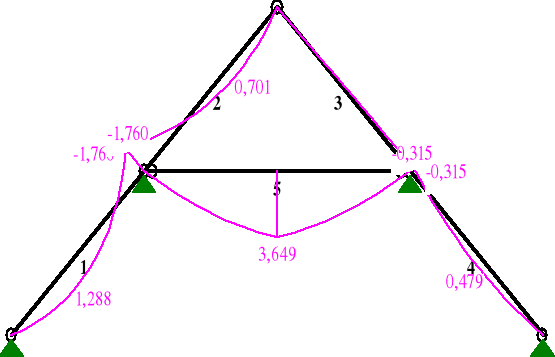
NORMALNE:

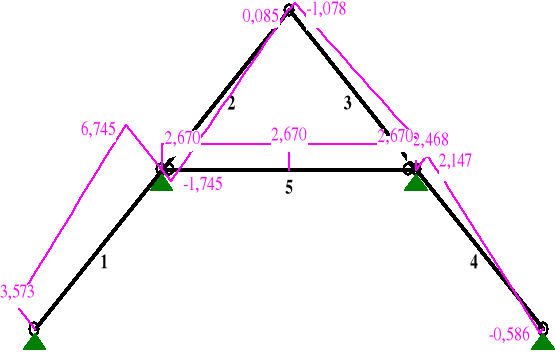
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: ABCDE

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 1,750 3,573

0,39 1,474 1,288* -0,003 4,825

1,00 3,737 -1,760 -2,692 6,745

2 0,00 0,000 -1,760 2,020 -1,745

0,65 2,438 0,701* -0,001 -0,551

1,00 3,738 0,000 -1,078 0,085

3 0,00 0,000 0,000 -0,085 -1,078

0,02 0,088 -0,007 -0,085* -1,111

1,00 3,736 -0,315 -0,084 -2,468

4 0,00 0,000 -0,315 0,755 2,147

0,56 2,102 0,479* 0,001 0,610

1,00 3,738 0,000 -0,586 -0,586

5 0,00 0,000 0,000 2,162 2,670

0,50 2,643 3,649* 0,600 2,670

0,50 2,643 3,649* -0,600 2,670

0,99 5,244 0,089 -2,138 2,670*

0,02 0,083 0,177 2,113 2,670*

1,00 5,285 0,000 -2,162 2,670

------------------------------------------------------------------

* = Wartości ekstremalne

REAKCJE PODPOROWE:

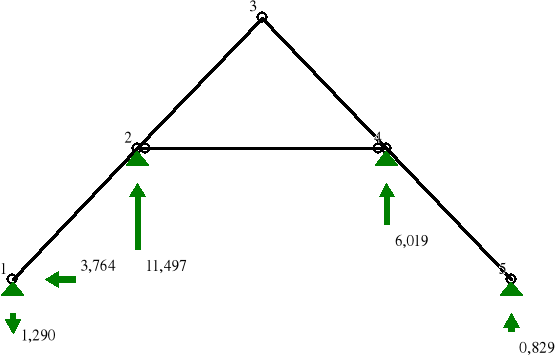
REAKCJE PODPOROWE: T.I rzędu

Obciążenia obl.: ABCDE

------------------------------------------------------------------

Węzeł: H[kN]: V[kN]: Wypadkowa[kN]: M[kNm]:

------------------------------------------------------------------

1 -3,764 -1,290 3,979

2 0,000 11,497 11,497

4 -0,000 6,019 6,019

5 0,000 0,829 0,829

------------------------------------------------------------------

1.2.4 Wymiarowanie krokwi

# Sprawdzenie stanu granicznego nośności

Maksymalny moment zginający i odpowiadająca mu siła podłużna:

M = 1,76 kNm

N = 6,745 kN

Warunku na zginanie i ściskanie (nad płatwią) nie sprawdziłam, ponieważ ponieważ krokiew jest zabezpieczona przed wyboczeniem w obu płaszczyznach.

Przyjęłam przekrój 80 × 180 mm,

A = b⋅h = 0,080 ⋅ 0,180 = 0,0144 m²= 14,4⋅10^-3m²,

W_y = b⋅h²/ 6 = 0,08⋅0,18²/6 = 4,32 ⋅10^-4 m²=432⋅10^-6 m²

• Sprawdzenie warunku na zginanie z osiową siłą rozciagajacą

σ_t,0,d / f_t,0,d + σ_m.,y,d / f_m,y,d + k_m ( σ_m.,z,d / f_m,z,d ) ≤ 1, gdzie:

k_mod = 0,9 - dla drewna litego i klasy trwania obciążenia = krótkotrwałe (wiatr ) oraz klasy użytkowania konstrukcji = 2 ,

γ_M = 1,3 - częściowy współczynnik bezpieczeństwa,

f_t,0,d = k_mod⋅f _t,0,k / γ_M= 0,9⋅18,0/1,3 = 12,461 MPa,

f_m,y,d = k_mod ⋅ f_m.,y,k / γ_M =0,9⋅30,0 / 1,3 = 20,77 MPa,

σ_t,0,d = N/A =6,745 / 14,4⋅10^-3 = 468,4 kPa = 0,468MPa,

σ_m.,y,d = M / W_y = 1,76 / 432⋅10^-6 = 4074,07 kPa = 4,074 MPa,

σ_m.,z,d = 0.

0,468 / 12,461 + 4,074 / 20,77 + 0 =0,23 < 1

Warunek SGN został spełniony.

# Sprawdzenie stanu granicznego użytkowalności

u_net.fin = L/200 = 3737/200 = 18,69 mm.

Po wykonaniu obliczeń w programie RM-Win otrzymałam następujące wartości ugięcia:

• od obciążenia ciężarem własnym

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"C.wł. łata+krok,kleszcze" Stałe 1,10

E -"Ciężar własny pokrycia" Stałe 1,20

------------------------------------------------------------------

PRZEMIESZCZENIA WĘZŁÓW: T.I rzędu

Obciążenia char.: AE

------------------------------------------------------------------

Węzeł: Ux[m]: Uy[m]: Wypadkowe[m]: Fi[rad]([deg]):

------------------------------------------------------------------

1 -0,00000 -0,00000 0,00000 -0,00189 ( -0,108)

2 0,00000 -0,00000 0,00000 0,00099 ( 0,057)

3 0,00001 -0,00001 0,00001

4 0,00001 -0,00000 0,00001 -0,00099 ( -0,057)

5 0,00001 -0,00000 0,00001 0,00189 ( 0,108)

------------------------------------------------------------------

PRZEMIESZCZENIA:

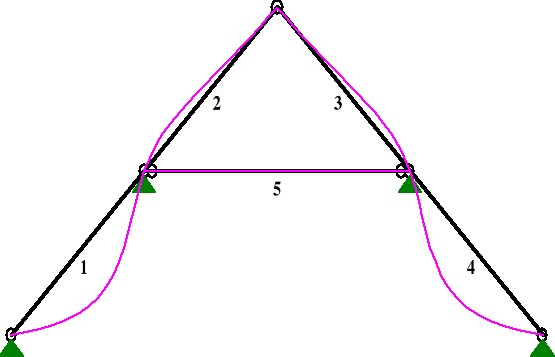
DEFORMACJE: T.I rzędu

Obciążenia char.: AE

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,108 0,057 0,0020 1865,8

2 -0,0000 -0,0000 0,057 -0,006 0,0004 8501,7

3 -0,0000 0,0000 0,006 -0,057 0,0004 8545,4

4 0,0000 0,0000 -0,057 0,108 0,0020 1865,8

5 -0,0000 -0,0000 -0,000 -0,000 0,0000 3,12E+21

-----------------------------------------------------------------

u_inst1 = 0,4 mm,

k_def = 0,8 (klasa trwania obciążenia = stałe, klasa użytkowania = 2 )

u_fin1 = u_inst1(1 + k_def ) = 0,72 mm.

• Od obciążenia śniegiem

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

B -"Śnieg" Zmienne 1 1,00 1,40

------------------------------------------------------------------

PRZEMIESZCZENIA:

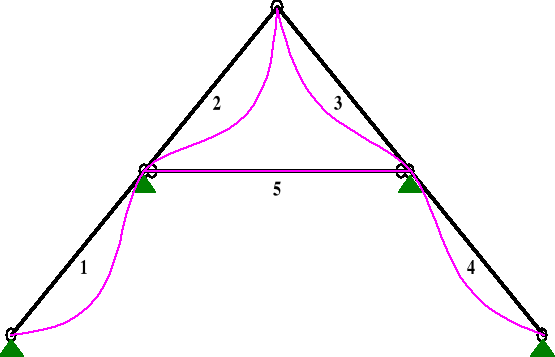
DEFORMACJE: T.I rzędu

Obciążenia char.: B

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,048 -0,000 0,0008 4621,7

2 -0,0000 -0,0000 -0,000 0,047 0,0008 4614,6

3 -0,0000 0,0000 -0,031 0,000 0,0005 6946,8

4 0,0000 0,0000 0,000 0,032 0,0005 6931,7

5 -0,0000 -0,0000 -0,000 -0,000 0,0000 1,56E+21

-----------------------------------------------------------------

u_inst = 0,8 mm,

k_def = 0,25 ( klasa trwania obciążenia = średnio-trwałe, klasa użytkowania = 2),

u_fin2 = u_inst (1 + k_def ) = 1,0 mm.

• Od obciążenia wiatrem

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

C -"Wiatr" Zmienne 1 1,00 1,30

PRZEMIESZCZENIA:

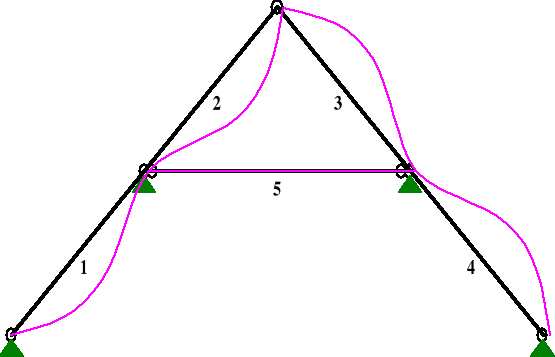
DEFORMACJE: T.I rzędu

Obciążenia char.: C

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0001 -0,051 -0,001 0,0008 4410,4

2 -0,0001 -0,0001 -0,001 0,049 0,0008 4405,6

3 0,0001 0,0001 0,055 0,000 0,0009 4059,0

4 0,0001 0,0001 0,000 -0,054 0,0009 4050,2

5 -0,0000 -0,0000 -0,000 -0,000 0,0000 1,95E+20

------------------------------------------------------------------

u_inst3 = 0,8 mm,

k_def = 0 (klasa trwania obciążenia = krótkotrwałe, klasa użytkowania = 2),

u_fin3 = u_inst3 (1+ k_def ) = 0,8 mm.

Ugięcie całkowite:

u_fin = u_fin1 + u_fin2 + u_fin3 = 0,72 + 1,0 + 0,8 = 2,52 mm

u_fin =7,66mm < u_net.fin = 18,69 mm.

Stan graniczny użytkowalności został spełniony.

1.2.5 Wymiarowanie kleszczy.

# Sprawdzenie stanu granicznego nośności

Moment zginający i siła podłużna:

M = 3,649 kNm

N = N_3-4 ⋅ n = 2,67 ⋅ 5 = 13,35 kN gdzie:

n - liczba wiązarów przypadająca na jedne kleszcze ,

Przyjęto przekrój 2× 50 × 140 mm,

A = 2⋅b⋅h = 2 ⋅ 0,05 ⋅ 0,14 = 0,014 m² = 14,00 ⋅10^-3 m²

Wy = 2⋅b⋅h²/6 = 2⋅0,05⋅ 0,14² / 6 = 3,27 10^-4 = 327 ⋅ 10^-6 m.

• Sprawdzenie warunku na zginanie z osiową siłą rozciągającą

σ_t,0,d / f_t,0,d + σ_m.,y,d / f_m,y,d + k_m ( σ_m.,z,d / f_m,z,d ) ≤ 1, gdzie:

k_mod = 0,9 - dla drewna litego i klasy trwania obciążenia = krótkotrwałe (wiatr ) oraz klasy użytkowania konstrukcji = 2 ,

γ_M = 1,3 - częściowy współczynnik bezpieczeństwa,

f_t,0,d = k_mod⋅f _t,0,k / γ_M= 0,9⋅18,0/1,3 = 12,461 MPa,

f_m,y,d = k_mod ⋅ f_m.,y,k / γ_M =0,9⋅30,0 / 1,3 = 20,77 MPa,

σ_t,0,d = N/A =13,35 / 14,4⋅10^-3 = 927,08 kPa = 0,927MPa,

σ_m.,y,d = M / W_y = 3,649 / 327 ⋅ 10^-6 = 11159,02 kPa = 11,159 MPa,

σ_m.,z,d = 0

0,927 / 12,461 + 11,159 / 20,77 + 0 =0,612 < 1

# Sprawdzenie stanu granicznego użytkowalności

unet.fin = L / 200 = 5285 / 200 = 26,4 mm.

Po wykonaniu obliczeń w programie RM-Win otrzymałam następujące ugięcia:

• Od obciążenia ciężarem własnym

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

A -"C.wł. łata+krok,kleszcze" Stałe 1,10

E -"Ciężar własny pokrycia" Stałe 1,20

------------------------------------------------------------------

PRZEMIESZCZENIA WĘZŁÓW: T.I rzędu

Obciążenia char.: AE

------------------------------------------------------------------

Węzeł: Ux[m]: Uy[m]: Wypadkowe[m]: Fi[rad]([deg]):

------------------------------------------------------------------

1 0,00000 0,00000 0,00000 -0,00000 ( -0,000)

2 0,00000 -0,00000 0,00000 -0,00000 ( -0,000)

3 0,00000 -0,00000 0,00000

4 0,00000 -0,00000 0,00000 0,00000 ( 0,000)

5 0,00000 0,00000 0,00000 -0,00000 ( -0,000)

------------------------------------------------------------------

PRZEMIESZCZENIA:

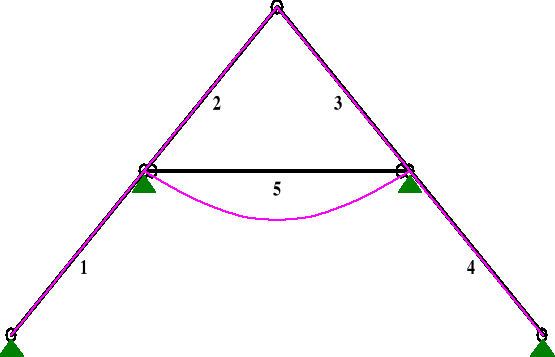
DEFORMACJE: T.I rzędu

Obciążenia char.: AE

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,000 -0,000 0,0000 2,35E+10

2 -0,0000 -0,0000 -0,000 -0,000 0,0000 2,35E+10

3 0,0000 0,0000 0,000 0,000 0,0000 4,92E+10

4 0,0000 0,0000 0,000 -0,000 0,0000 4,92E+10

5 -0,0000 -0,0000 -0,641 0,641 0,0185 286,1

------------------------------------------------------------------

u_inst1 = 18,5 mm,

k_def = 0,8 ( klasa trwania obciążenia = stałe, klasa użytkowania = 2 ),

u_fin1 = u_inst1 ( 1 + k_def ) = 33,3 mm.

• Od obciążenia siłą skupioną (człowiek )

==================================================================

W Y N I K I

Teoria I-go rzędu

==================================================================

OBCIĄŻENIOWE WSPÓŁ. BEZPIECZ.:

------------------------------------------------------------------

Grupa: Znaczenie: d: γf:

------------------------------------------------------------------

D -"Człowiek" Zmienne 1 1,00 1,20

------------------------------------------------------------------

PRZEMIESZCZENIA:

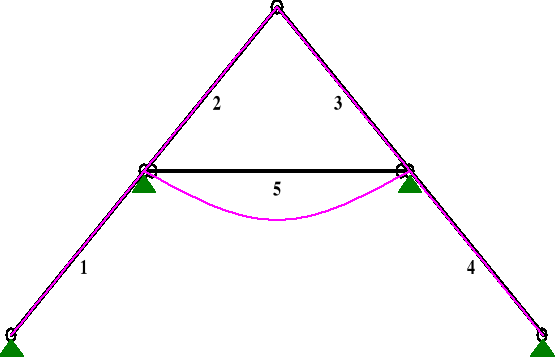
DEFORMACJE: T.I rzędu

Obciążenia char.: D

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0000 -0,000 -0,000 0,0000 9,56E+09

2 -0,0000 -0,0000 -0,000 -0,000 0,0000 9,56E+09

3 0,0000 0,0000 0,000 0,000 0,0000 2,00E+10

4 0,0000 0,0000 0,000 -0,000 0,0000 2,00E+10

5 -0,0000 -0,0000 -0,365 0,365 0,0112 471,6

------------------------------------------------------------------

u_inst2 = 11,2 mm,

k_def = 0 ( klasa trwania obciążenia = krótko-trwałe, klasa użytkowania = 2 ),

u_fin2 = u_inst2 (1 + k_def ) = 11,2 mm.

Ugięcie całkowite :

u_fin = u_fin1 + u_fin2 = 33,3 + 11,2 = 44,5 mm,

u_fin = 44,5 mm > unet.fin = 26,4 mm

Stan graniczny użytkowalności nie został spełniony.

1.2.6 Wymiarowanie płatwi.

Przyjęto przekrój 120×150 mm,

A = b⋅h = 120⋅150 = 18 000 mm² = 0,018 m²,

W_y = bh²/6 = 120⋅150²/6 = 450,0 ⋅10³ mm³ = 4,5 ⋅10^-4 m³,

W_z = hb²/6 = 150⋅120²/6 = 360,0 mm³ = 3,6⋅10^-4 m³.

S_z = S cosα,

p_z = p_kcosα,

p_y = p_k sinα.

Tabela 1.3 Zestawienie obciążeń na płatew

Obciążenie	Wartość charaktery- styczne [kN/m]	Współ- czynnik obciążenia γF	Wartość obliczeniowa	Składowa pionowa obciążenia (z) na długości krokwi		Składowa pozioma obciążenia (y) na długości krokwi
								wartość charaktery- styczna [kN/m]	wartość obliczenio-wa [kN/m]	wartość charaktery- styczna [kN/m]	wartość obliczenio-wa [kN/m]
Ciężar własny pokrycia z uwzględnieniem ciężaru krokwi blacha trapezowa 0,091⋅0,8 m, łaty 0,016⋅2⋅0,8m, ciężar własny krokwi 0,08⋅0,160⋅5,5 wełny mineralnej 0,15⋅2⋅0,8 płyty gipsowo-kartonowej 0,019⋅12,0⋅0,8 RAZEM: Ciężar własny płatwi 0,12⋅0,15⋅5,5⋅0,8m Śnieg Sk = Qk⋅C =1,05⋅0,6⋅0,8m Wiatr połać nawietrzna pk = qk⋅Cc⋅C⋅β = =0,425⋅0,8⋅0,475⋅1,8⋅0,8m	0,0728 0,0256 0,0701 0,24 0,182 gk = 0,591 gkp = 0,099 Sk = 0,504* pk = +0,233	1,2 1,1 1,1 1,2 1,2 1,1 1,4 1,3	0,0874 0,0282 0,0771 0,288 0,219 gd = 0,7 gdp = 0,109 Sd = 0,706* pd = 0,3023	0,0728 0,0256 0,0701 0,24 0,182 gkz = 0,591 gkpz=0,099 Skz =0,356 pkz = 0,165 **	0,0874 0,0282 0,0771 0,288 0,219 gdz = 0,7 gdpz=0,109 Sdz = 0,5 pdz =0,214 **	- - - - - gky = 0 gkpy = 0 Sky = 0 pky = 0,165 **	- - - - - gdy = 0 gdpy = 0 Sdy = 0 pdy =0,214 **

* Wartość na 1 m² powierzchni dachu

** Uwzględniono współczynnik jednoczesności obciążeń ψ_° = 0,9

Na płatew działa obciążenie z pasa szerokości 3,737 + 0,5 ⋅ 3,737 ( odcinek górny + połowa dolnego odcinka krokwi).

• składowa pionowa obciążenia

q_kz=(g_kz+S_kz+p_kz)(3,737 + 0,5⋅3,737)+g_kpz= (0,591+0,356+0,165 )(3,737+0,5⋅3,737)+0,099 =

= 6,332 kN/m,

q_dz = (g_dz+S_dz+p_dz)(3,737+0,5⋅3,737)+g_dpz = (0,7+0,5+0,214)(3,737+0,5⋅3,737)+0,109 =

=8,032 kN/m

• składowa pozioma obciążenia

q_ky = p_ky(3,737 + 0,5 ⋅ 3,737) = 0,165⋅(3,737+0,5⋅3,737) = 0,925 kN/m.

q_dy = p_dy⋅(3,737+0,5⋅3,737) = 0,214⋅(3,737+0,5⋅3,737) = 1,2 kN/m.

# Sprawdzenie stanu granicznego nośności

Wyznaczenie sił wewnętrznych

Obliczeń dokonałam przy użyciu programu RM-Win.

Płaszczyzna pionowa - rama o schemacie statycznym na rysunku poniżej

PRĘTY:

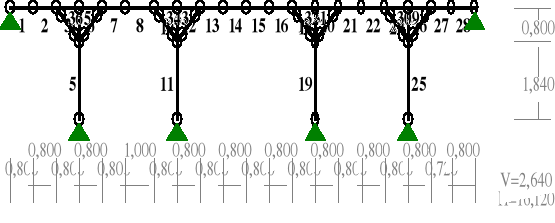
PRZEKROJE PRĘTÓW:

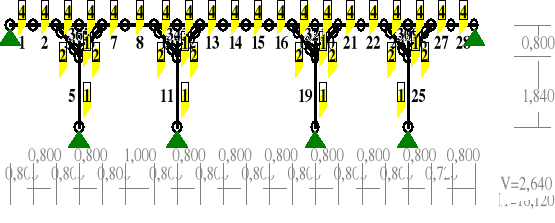
PRĘTY UKŁADU:

Typy prętów: 00 - sztyw.-sztyw.; 01 - sztyw.-przegub;

10 - przegub-sztyw.; 11 - przegub-przegub

22 - cięgno

------------------------------------------------------------------

Pręt: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ: Przekrój:

------------------------------------------------------------------

1 10 1 2 0,800 0,000 0,800 1,000 4 B 150x120

2 00 2 3 0,800 0,000 0,800 1,000 4 B 150x120

3 01 3 4 0,800 0,000 0,800 1,000 4 B 150x120

4 10 4 5 0,000 -0,800 0,800 1,000 1 B 150x150

5 01 5 6 0,000 -1,840 1,840 1,000 1 B 150x150

6 10 4 7 0,800 0,000 0,800 1,000 4 B 150x120

7 00 7 8 0,800 0,000 0,800 1,000 4 B 150x120

8 00 8 9 1,000 0,000 1,000 1,000 4 B 150x120

9 01 9 10 0,800 0,000 0,800 1,000 4 B 150x120

10 10 10 11 0,000 -0,800 0,800 1,000 1 B 150x150

11 01 11 12 0,000 -1,840 1,840 1,000 1 B 150x150

12 10 10 13 0,800 0,000 0,800 1,000 4 B 150x120

13 00 13 14 0,800 0,000 0,800 1,000 4 B 150x120

14 00 14 15 0,800 0,000 0,800 1,000 4 B 150x120

15 00 15 16 0,800 0,000 0,800 1,000 4 B 150x120

16 00 16 17 0,800 0,000 0,800 1,000 4 B 150x120

17 01 17 18 0,800 0,000 0,800 1,000 4 B 150x120

18 10 18 19 0,000 -0,800 0,800 1,000 1 B 150x150

19 01 19 20 0,000 -1,840 1,840 1,000 1 B 150x150

20 10 18 21 0,800 0,000 0,800 1,000 4 B 150x120

21 00 21 22 0,800 0,000 0,800 1,000 4 B 150x120

22 00 22 23 0,800 0,000 0,800 1,000 4 B 150x120

23 01 23 24 0,800 0,000 0,800 1,000 4 B 150x120

24 10 24 25 0,000 -0,800 0,800 1,000 1 B 150x150

25 10 26 25 0,000 1,840 1,840 1,000 1 B 150x150

26 10 24 27 0,800 0,000 0,800 1,000 4 B 150x120

27 00 27 28 0,720 0,000 0,720 1,000 4 B 150x120

28 01 28 29 0,800 0,000 0,800 1,000 4 B 150x120

29 11 27 25 -0,800 -0,800 1,131 1,000 2 B 100x100

30 11 25 23 -0,800 0,800 1,131 1,000 2 B 100x100

31 11 21 19 -0,800 -0,800 1,131 1,000 2 B 100x100

32 11 19 17 -0,800 0,800 1,131 1,000 2 B 100x100

33 11 13 11 -0,800 -0,800 1,131 1,000 2 B 100x100

34 11 11 9 -0,800 0,800 1,131 1,000 2 B 100x100

35 11 7 5 -0,800 -0,800 1,131 1,000 2 B 100x100

36 11 5 3 -0,800 0,800 1,131 1,000 2 B 100x100

------------------------------------------------------------------

WIELKOŚCI PRZEKROJOWE:

------------------------------------------------------------------

Nr. A[cm2] Ix[cm4] Iy[cm4] Wg[cm3] Wd[cm3] h[cm] Materiał:

------------------------------------------------------------------

1 225,0 4219 4219 563 563 15,0 25 c30

2 100,0 833 833 167 167 10,0 25 c30

4 180,0 3375 2160 450 450 15,0 25 c30

------------------------------------------------------------------

STAŁE MATERIAŁOWE:

------------------------------------------------------------------

Materiał: Moduł E: Napręż.gr.: AlfaT:

[N/mm2] [N/mm2] [1/K]

------------------------------------------------------------------

25 c30 12000 18,000 0,00E+00

------------------------------------------------------------------

OBCIĄŻENIA:

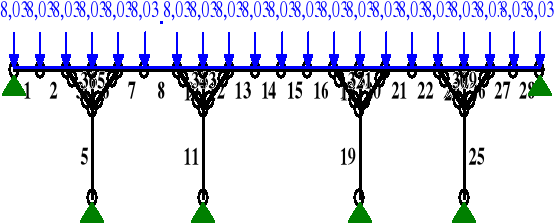
MOMENTY:

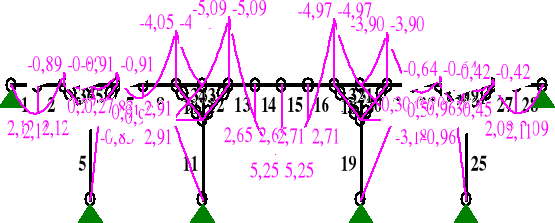
NORMALNE

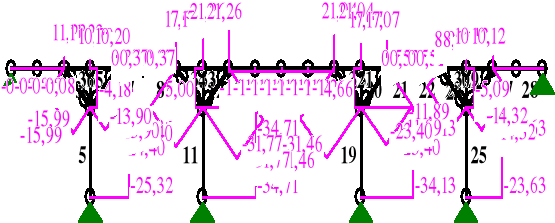
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: A

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,00 5,87 -0,08

0,91 0,731 2,14* -0,00 -0,08

1,00 0,800 2,12 -0,56 -0,08

2 0,00 0,000 2,12 -0,56 -0,08

1,00 0,800 -0,89 -6,98 -0,08

3 0,00 0,000 -0,89 4,33 11,23

0,68 0,541 0,27* -0,02 11,23

0,67 0,538 0,27* 0,01 11,23

1,00 0,800 0,00 -2,10 11,23

4 0,00 0,000 0,00 -1,03 -4,18

1,00 0,800 -0,83 -1,03 -4,18

5 0,00 0,000 -0,83 0,45 -25,32

1,00 1,840 0,00 0,45 -25,32

6 0,00 0,000 0,00 2,08 10,20

0,32 0,259 0,27* -0,00 10,20

1,00 0,800 -0,91 -4,35 10,20

7 0,00 0,000 -0,91 5,48 0,37

0,86 0,684 0,96* -0,01 0,37

0,85 0,681 0,96* 0,01 0,37

1,00 0,800 0,91 -0,94 0,37

8 0,00 0,000 0,91 -0,94 0,37

1,00 1,000 -4,05 -8,98 0,37

9 0,00 0,000 -4,05 8,28 17,62

1,00 0,800 0,00 1,85 17,62

10 0,00 0,000 0,00 3,63 5,00

1,00 0,800 2,91 3,63 5,00

11 0,00 0,000 2,91 -1,58 -34,71

1,00 1,840 -0,00 -1,58 -34,71

12 0,00 0,000 0,00 -3,15 21,26

1,00 0,800 -5,09 -9,58 21,26

13 0,00 0,000 -5,09 12,89 -1,21

1,00 0,800 2,65 6,46 -1,21

14 0,00 0,000 2,65 6,46 -1,21

1,00 0,800 5,25 0,04 -1,21

15 0,00 0,000 5,25 0,04 -1,21

0,01 0,006 5,25* -0,01 -1,21

0,00 0,003 5,25* 0,01 -1,21

1,00 0,800 2,71 -6,39 -1,21

16 0,00 0,000 2,71 -6,39 -1,21

1,00 0,800 -4,97 -12,81 -1,21

17 0,00 0,000 -4,97 9,43 21,04

1,00 0,800 0,00 3,00 21,04

18 0,00 0,000 0,00 -3,97 4,66

1,00 0,800 -3,18 -3,97 4,66

19 0,00 0,000 -3,18 1,73 -34,13

1,00 1,840 0,00 1,73 -34,13

20 0,00 0,000 0,00 -1,66 17,07

1,00 0,800 -3,90 -8,08 17,07

21 0,00 0,000 -3,90 8,46 0,52

1,00 0,800 0,30 2,03 0,52

22 0,00 0,000 0,30 2,03 0,52

0,32 0,253 0,56* 0,00 0,52

1,00 0,800 -0,64 -4,39 0,52

23 0,00 0,000 -0,64 4,02 8,93

0,63 0,500 0,36* -0,00 8,93

1,00 0,800 -0,00 -2,41 8,93

24 0,00 0,000 0,00 1,20 -5,09

1,00 0,800 0,96 1,20 -5,09

25 0,00 0,000 0,00 -0,52 -23,63

1,00 1,840 -0,96 -0,52 -23,63

26 0,00 0,000 0,00 2,68 10,12

0,42 0,334 0,45* -0,00 10,12

1,00 0,800 -0,42 -3,74 10,12

27 0,00 0,000 -0,42 6,38 -0,00

1,00 0,720 2,09 0,60 -0,00

28 0,00 0,000 2,09 0,60 0,00

0,09 0,075 2,11* -0,00 0,00

1,00 0,800 0,00 -5,83 0,00

29 0,00 0,000 0,00 0,00 -14,32

1,00 1,131 0,00 0,00 -14,32

30 0,00 0,000 0,00 0,00 -11,89

1,00 1,131 0,00 0,00 -11,89

31 0,00 0,000 0,00 0,00 -23,40

1,00 1,131 0,00 0,00 -23,40

32 0,00 0,000 0,00 0,00 -31,46

1,00 1,131 0,00 0,00 -31,46

33 0,00 0,000 0,00 0,00 -31,77

1,00 1,131 0,00 0,00 -31,77

34 0,00 0,000 0,00 0,00 -24,40

1,00 1,131 0,00 0,00 -24,40

35 0,00 0,000 0,00 0,00 -13,90

1,00 1,131 0,00 0,00 -13,90

36 0,00 0,000 0,00 0,00 -15,99

1,00 1,131 0,00 0,00 -15,99

------------------------------------------------------------------

* = Wartości ekstremalne

Płaszczyzna pozioma

WĘZŁY:

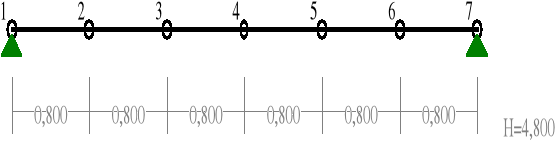
PRĘTY:

PRZEKROJE PRĘTÓW:

PRĘTY UKŁADU:

------------------------------------------------------------------

Pręt: Typ: A: B: Lx[m]: Ly[m]: L[m]: Red.EJ: Przekrój:

------------------------------------------------------------------

1 00 1 2 0,800 0,000 0,800 1,000 1 B 150x120

2 00 2 3 0,800 0,000 0,800 1,000 1 B 150x120

3 00 3 4 0,800 0,000 0,800 1,000 1 B 150x120

4 00 4 5 0,800 0,000 0,800 1,000 1 B 150x120

5 00 5 6 0,800 0,000 0,800 1,000 1 B 150x120

6 00 6 7 0,800 0,000 0,800 1,000 1 B 150x120

------------------------------------------------------------------

WIELKOŚCI PRZEKROJOWE:

------------------------------------------------------------------

Nr. A[cm2] Ix[cm4] Iy[cm4] Wg[cm3] Wd[cm3] h[cm] Materiał:

------------------------------------------------------------------

1 180,0 3375 2160 450 450 15,0 25 c30

------------------------------------------------------------------

OBCIĄŻENIA:

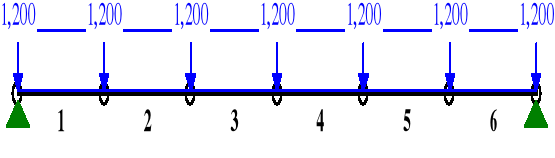
OBCIĄŻENIA: ([kN],[kNm],[kN/m])

------------------------------------------------------------------

Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]:

------------------------------------------------------------------

Grupa: A "" Zmienne γf= 1,00

1 Liniowe 0,0 1,200 1,200 0,00 0,80

2 Liniowe 0,0 1,200 1,200 0,00 0,80

3 Liniowe 0,0 1,200 1,200 0,00 0,80

4 Liniowe 0,0 1,200 1,200 0,00 0,80

5 Liniowe 0,0 1,200 1,200 0,00 0,80

6 Liniowe 0,0 1,200 1,200 0,00 0,80

------------------------------------------------------------------

MOMENTY:

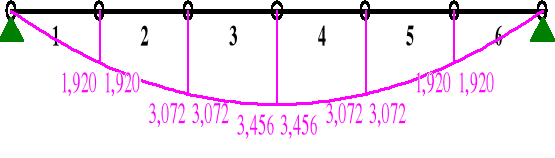
SIŁY PRZEKROJOWE: T.I rzędu

Obciążenia obl.: A

------------------------------------------------------------------

Pręt: x/L: x[m]: M[kNm]: Q[kN]: N[kN]:

------------------------------------------------------------------

1 0,00 0,000 0,000 2,880 0,000

1,00 0,800 1,920 1,920 0,000

2 0,00 0,000 1,920 1,920 0,000

1,00 0,800 3,072 0,960 0,000

3 0,00 0,000 3,072 0,960 0,000

1,00 0,797 3,456* 0,004 0,000

1,00 0,800 3,456 0,000 0,000

4 0,00 0,000 3,456 -0,000 0,000

0,00 0,003 3,456* -0,004 0,000

1,00 0,800 3,072 -0,960 0,000

5 0,00 0,000 3,072 -0,960 0,000

1,00 0,800 1,920 -1,920 0,000

6 0,00 0,000 1,920 -1,920 0,000

1,00 0,800 0,000 -2,880 0,000

------------------------------------------------------------------

* = Wartości ekstremalne

Najbardziej wytężony jest przekrój 14-15, w którym:

M_y = 5,25 kNm

N = - 1,21 kN

M_z = 3,456 kNm

k_mod = 0,9 - dla drewna litego i klasy trwania obciążenia= krótkotrwałe (wiatr) oraz klasy użytkowania konstrukcji = 2

γ_M. = 1,3 - częściowy współczynnik bezpieczeństwa

f_t,0,d = f_t,0,k*k_mod / γ_M = 18*0,9 /1,3 = 12,46 Mpa,

f_t,y,d = f_t,y,d = f_m.,k * k_mod / γ_M. = 30*0,9 / 1,3 = 20,77 MPa ,

σ_t,0,d = N/A = -1,21*10³ / 18000 = −0,067 MPa

σ_m,y,d = M_y /W_y = 5,25*10⁶ / (450*10³ ) = 11,67 MPa

σ_m,z,d = M_z /W_z = 3,456 *10⁶ / (360*10³ ) = 9,6 MPa

Zginanie z osiową siłą ściskającą

(σ_t,0,d / f_t,0,d )²+ σ_m.,y,d / f_m,y,d + k_m ( σ_m.,z,d / f_m,z,d ) ≤ 1,

lub: (σ_t,0,d / f_t,0,d )²+ k_m ( σ_m.,y,d / f_m,y,d )+ σ_m.,z,d / f_m,z,d ≤ 1,

gdzie k_m =0,7 dla przekrojow prostokatnych

(−0,067/12,46 )² + 11,67/20,77 + 0,7*( 9,6/20,77) = −0,00003 + 0,562 + 0,32 = 0,88 ≤ 1

(−0,067/12,46 )² + 0,7*( 11,67/20,77) + 9,6/20,77 = −0,00003 + 0,39 + 0,46 = 0,85 ≤ 1

Warunek SGN zostal spelniony.

# Sprawdzenie stanu granicznego użytkowalności

I_z = bh³/12 = 120⋅150³/12 = 3375⋅10⁴ mm⁴

Iy =b³h/12 = 120³⋅150/12 = 2160⋅10⁴ mm⁴

E_0,mean = 12000 MPa

Ugięcie od obciążenia ciężarem własnym i pokrycia:

k_def = 0,8 (klasa trwania obciążenia = stałe, klasa użytkowania = 2 )

q_klz = g_kz⋅(3,737 + 0,5 ⋅ 3,737) + g_kpz = 0,591⋅(3,737 + 0,5 ⋅ 3,737) + 0,099 = 3,41 kN/m

OBCIĄŻENIA:

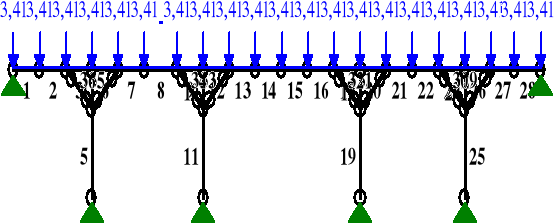
PRZEMIESZCZENIA:

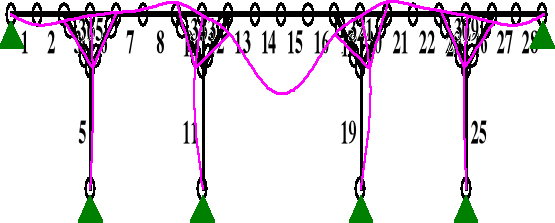
DEFORMACJE: T.I rzędu

Obciążenia obl.: A

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0008 -0,087 -0,015 0,0001 5907,6

2 -0,0008 -0,0005 -0,015 0,035 0,0001 7986,4

3 -0,0005 -0,0001 0,035 0,034 0,0000 84544,4

4 0,0000 0,0004 0,029 0,013 0,0000 28164,6

5 0,0004 -0,0000 0,013 -0,023 0,0002 12245,5

6 -0,0001 0,0002 0,015 0,013 0,0000 89628,7

7 0,0002 0,0004 0,013 0,034 0,0000 16796,1

8 0,0004 0,0009 0,034 -0,020 0,0001 8320,9

9 0,0009 -0,0001 -0,020 -0,097 0,0001 6111,4

10 0,0001 -0,0012 -0,106 -0,050 0,0001 7998,8

11 -0,0012 -0,0000 -0,050 0,079 0,0005 3477,7

12 -0,0001 -0,0015 -0,072 -0,174 0,0002 4564,4

13 -0,0015 -0,0047 -0,174 -0,212 0,0001 9365,6

14 -0,0047 -0,0063 -0,212 -0,002 0,0004 2127,6

15 -0,0063 -0,0047 -0,002 0,210 0,0004 2113,8

16 -0,0047 -0,0016 0,210 0,176 0,0001 10055,1

17 -0,0016 -0,0001 0,176 0,077 0,0002 4698,7

18 0,0001 0,0014 0,111 0,050 0,0001 7318,0

19 0,0014 -0,0000 0,050 -0,090 0,0006 3181,7

20 -0,0001 0,0010 0,100 0,027 0,0001 6430,2

21 0,0010 0,0007 0,027 -0,039 0,0001 7042,6

22 0,0007 0,0003 -0,039 -0,026 0,0000 25346,8

23 0,0003 -0,0001 -0,026 -0,021 0,0000 42886,0

24 0,0002 -0,0003 -0,038 -0,020 0,0000 24285,9

25 0,0000 0,0003 0,023 -0,020 0,0002 10559,1

26 -0,0001 -0,0006 -0,045 -0,035 0,0000 29275,7

27 -0,0006 -0,0008 -0,035 0,016 0,0001 8167,2

28 -0,0008 0,0000 0,016 0,087 0,0001 5972,5

29 0,0006 -0,0001 -0,036 -0,036 0,0000 1,27E+15

30 0,0002 -0,0003 -0,028 -0,028 0,0000 8,49E+14

31 -0,0006 0,0011 0,084 0,084 0,0000 6,37E+14

32 -0,0009 0,0011 0,100 0,100 0,0000 1,27E+15

33 0,0011 -0,0007 -0,096 -0,096 0,0000 6,37E+14

34 0,0009 -0,0007 -0,080 -0,080 0,0000 6,37E+14

35 -0,0001 0,0003 0,020 0,020 0,0000 5,10E+15

36 -0,0002 0,0004 0,028 0,028 0,0000 2,55E+15

-----------------------------------------------------------------

u _inst,1,z = 0,4 mm

u _fin,1,z = u _inst,1,z (1+ k_def ) = 0,4 (1+0,8) = 1,62 mm

Ugięcie od obciążenia śniegiem:

k_def = 0,25 (klasa trwania obciążenia = średniotrwałe, klasa użytkowania = 2)

q_k2z = S_kz ⋅(3,737 + 0,5 ⋅ 3,737) = 0,356⋅(3,737 + 0,5 ⋅ 3,737) =2,00kN/m.

OBCIĄŻENIA:

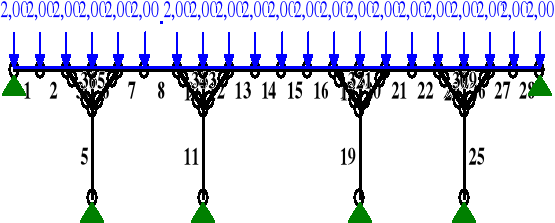
PRZEMIESZCZENIA:

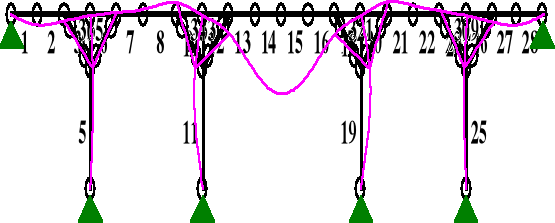
DEFORMACJE: T.I rzędu

Obciążenia char.: B

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0005 -0,051 -0,009 0,0001 10072,5

2 -0,0005 -0,0003 -0,009 0,021 0,0001 13616,8

3 -0,0003 -0,0000 0,021 0,020 0,0000 144148,3

4 0,0000 0,0002 0,017 0,008 0,0000 48020,7

5 0,0002 0,0000 0,008 -0,014 0,0001 20878,6

6 -0,0000 0,0001 0,009 0,008 0,0000 152816,9

7 0,0001 0,0002 0,008 0,020 0,0000 28637,3

8 0,0002 0,0006 0,020 -0,012 0,0001 14187,1

9 0,0006 -0,0001 -0,012 -0,057 0,0001 10419,9

10 0,0000 -0,0007 -0,062 -0,029 0,0001 13637,9

11 -0,0007 -0,0000 -0,029 0,046 0,0003 5929,5

12 -0,0001 -0,0009 -0,042 -0,102 0,0001 7782,3

13 -0,0009 -0,0027 -0,102 -0,124 0,0001 15968,4

14 -0,0027 -0,0037 -0,124 -0,001 0,0002 3627,6

15 -0,0037 -0,0028 -0,001 0,123 0,0002 3604,0

16 -0,0028 -0,0009 0,123 0,103 0,0000 17143,9

17 -0,0009 -0,0001 0,103 0,045 0,0001 8011,3

18 0,0001 0,0008 0,065 0,030 0,0001 12477,2

19 0,0008 0,0000 0,030 -0,053 0,0003 5424,9

20 -0,0001 0,0006 0,059 0,016 0,0001 10963,5

21 0,0006 0,0004 0,016 -0,023 0,0001 12007,6

22 0,0004 0,0002 -0,023 -0,015 0,0000 43216,2

23 0,0002 -0,0000 -0,015 -0,012 0,0000 73120,6

24 0,0001 -0,0002 -0,022 -0,011 0,0000 41407,4

25 0,0000 0,0002 0,013 -0,011 0,0001 18003,2

26 -0,0000 -0,0004 -0,026 -0,020 0,0000 49915,1

27 -0,0004 -0,0005 -0,020 0,010 0,0001 13925,1

28 -0,0005 0,0000 0,010 0,051 0,0001 10183,1

29 0,0003 -0,0001 -0,021 -0,021 0,0000 2,55E+15

30 0,0001 -0,0002 -0,017 -0,017 0,0000 1,70E+15

31 -0,0004 0,0006 0,049 0,049 0,0000 1,27E+15

32 -0,0005 0,0006 0,059 0,059 0,0000 1,27E+15

33 0,0007 -0,0004 -0,056 -0,056 0,0000 1,27E+15

34 0,0005 -0,0004 -0,047 -0,047 0,0000 1,27E+15

35 -0,0001 0,0002 0,012 0,012 0,0000 4,08E+15

36 -0,0001 0,0002 0,017 0,017 0,0000 1,02E+16

------------------------------------------------------------------

u_inst,2,z = 0,2 mm

u_fin,2,z = u_inst,2,z (1+ k_def ) = 0,2 (1+0,25) = 0,25 mm

Ugięcie od obciążenia pionowego wiatrem:

k_def =0 (klasa trwania obciążenia = krótkotrwałe, klasa użytkowania = 2)

q_k3z = p_kz ⋅(3,737 + 0,5 ⋅ 3,737) = 0,165⋅(3,737 + 0,5 ⋅ 3,737) =0,925 kN/m.

OBCIĄŻENIA:

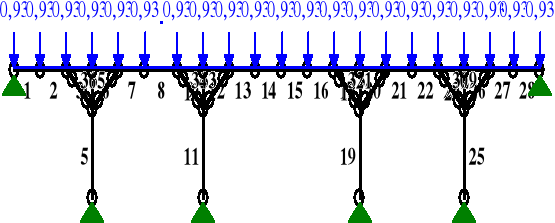
PRZEMIESZCZENIA:

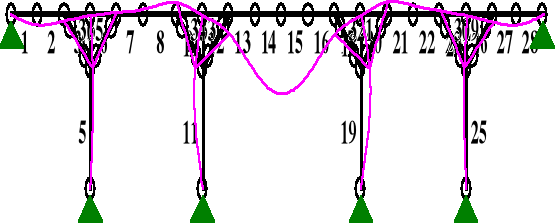
DEFORMACJE: T.I rzędu

Obciążenia char.: C

------------------------------------------------------------------

Pręt: Wa[m]: Wb[m]: FIa[deg]: FIb[deg]: f[m]: L/f:

------------------------------------------------------------------

1 -0,0000 -0,0002 -0,023 -0,004 0,0000 21778,4

2 -0,0002 -0,0001 -0,004 0,010 0,0000 29441,8

3 -0,0001 -0,0000 0,010 0,009 0,0000 311671,9

4 0,0000 0,0001 0,008 0,004 0,0000 103828,5

5 0,0001 0,0000 0,004 -0,006 0,0000 45142,8

6 -0,0000 0,0000 0,004 0,004 0,0000 330415,0

7 0,0000 0,0001 0,004 0,009 0,0000 61918,4

8 0,0001 0,0003 0,009 -0,005 0,0000 30674,9

9 0,0003 -0,0000 -0,005 -0,026 0,0000 22529,4

10 0,0000 -0,0003 -0,029 -0,014 0,0000 29487,4

11 -0,0003 -0,0000 -0,014 0,021 0,0001 12820,6

12 -0,0000 -0,0004 -0,020 -0,047 0,0000 16826,6

13 -0,0004 -0,0013 -0,047 -0,058 0,0000 34526,2

14 -0,0013 -0,0017 -0,058 -0,001 0,0001 7843,5

15 -0,0017 -0,0013 -0,001 0,057 0,0001 7792,4

16 -0,0013 -0,0004 0,057 0,048 0,0000 37067,9

17 -0,0004 -0,0000 0,048 0,021 0,0000 17321,7

18 0,0000 0,0004 0,030 0,014 0,0000 26977,7

19 0,0004 0,0000 0,014 -0,024 0,0002 11729,4

20 -0,0000 0,0003 0,027 0,007 0,0000 23704,9

21 0,0003 0,0002 0,007 -0,011 0,0000 25962,4

22 0,0002 0,0001 -0,011 -0,007 0,0000 93440,5

23 0,0001 -0,0000 -0,007 -0,006 0,0000 158098,6

24 0,0000 -0,0001 -0,010 -0,005 0,0000 89529,5

25 0,0000 0,0001 0,006 -0,005 0,0000 38925,9

26 -0,0000 -0,0002 -0,012 -0,009 0,0000 107924,6

27 -0,0002 -0,0002 -0,009 0,004 0,0000 30108,4

28 -0,0002 0,0000 0,004 0,024 0,0000 22017,5

29 0,0002 -0,0000 -0,010 -0,010 0,0000 5,10E+15

30 0,0001 -0,0001 -0,008 -0,008 0,0000 5,10E+15

31 -0,0002 0,0003 0,023 0,023 0,0000 2,55E+15

32 -0,0002 0,0003 0,027 0,027 0,0000 1,27E+15

33 0,0003 -0,0002 -0,026 -0,026 0,0000 2,55E+15

34 0,0002 -0,0002 -0,022 -0,022 0,0000 2,55E+15

35 -0,0000 0,0001 0,005 0,005 0,0000 8,15E+15

36 -0,0001 0,0001 0,008 0,008 0,0000 6,79E+15

------------------------------------------------------------------

u _inst,3,z = 0,1 mm

u _fin,3,z = u _inst,3,z (1+ k _def ) = 0,1(1+0) = 0,1mm

Ugięcie od obciążenia poziomego wiatrem:

k _def = 0 (klasa trwania obciążenia = krótkotrwałe, klasa użytkowania = 2)

q_ky = p_ky ⋅(3,737 + 0,5 ⋅ 3,737) = 0,165*5,61 = 0,925 kN/m.

l_y = 4,8m., h = 0,15 m; l_y /h = 4,8/0,15 = 32

u_inst,y = 5 q_ky l_y⁴ / 384 E_0,mean I_y = ( 5*0,925* 4800⁴)/(384*12000*2160*10⁴ ) = 24,7mm

u_fin,y = u_inst,y (1+ k _def ) = 24,7mm

Ugięcie finalne:

u_inst,z = u_inst,,1,z + u_inst,2,z +u_inst,3,z = 0,4 + 0,2 + 0,1 = 0,7 mm

u_inst,y = 24,7mm

u_inst = pierwiastek(u_inst,z ² + u_inst,y ² ) = 24,71 mm

u_fin,z = u_fin,1,z * u_fin,2,z * u_fint,3,z = 0,72 + 0,25 + 0,1 = 1,07 mm

u_fin,y = 24,7mm

u_fin = pierwiastek(u_fin,z ² + u_fin,y ² ) = 24,73 mm

u_fin = 24,73 mm > u_net,fin = l/200 = 4800 / 200 = 24 mm

Obliczone ugięcie jest większe od ugięcia dopuszczalnego. Warunek SGU nie został spełniony.

1.2.7 Wymiarowanie słupa

Słup jest ściskany osiowo siłą P=34,38 kN

Przyjęto przekrój słupa 180 × 140mm

A_d = 150*150 = 22500mm²

I_y = I_z = a⁴ /12 = 150⁴ /12 = 4218,75*10⁴ mm⁴

i = pierwiastek( I /A ) = 43,3 mm,

l_y = 2640 mm,

l_z = 1840 mm,

λ_y = l_y / i_y = 2640 / 43,3 = 61,00 − smuklosc wyględem osi y

σ_c,crit,y = π²*E_0,05 / λ²_y

σ_c,crit,y = π²*8000 / 61² = 21,2 MPa,

λ_rel,y =pierwiastek( f _c,0,k / σ_c,crit,y ) = 1,04, f _c,0,k = 23,00

k_y = 0,5[1 + β_c (λ_rel,y - 0,5) +λ²_rel,y ]

β_c - wspol. dotyczacy prostoliniowosci elementow ( dla drewna litego β_c = 0,2 )

k_y = 0,5[1 + 0,2*(1,04 - 0,5) +1,04²] = 1,095

k_c,y = 1 / [k_y + pierw( k_y² - +λ²_rel,y )]

k_c,y = 1 / [ 1,095 + pierw( 1,095² - 1,04²) = 0,695

σ_c,0,d = P / A_d = 34,38*10³ / 22500 = 1,528 MPa

Stan graniczny nosnosci slupow osiowo sciskanych :

(σ_c,0,d / k_c,y*f_c,0,d )²+ σ_m.,y,d / f_m,y,d + k_m ( σ_m.,z,d / f_m,z,d ) ≤ 1,

f_c,0,d = f_c,0,k * k_mod / γ_M. = 23*0,9 / 1,3 = 15,92 MPa

(1,528 / 0,695*15,92 )²+ 0 + 0 = 0,14 < 1,

Warunek SGN zostal spelniony

Sprawdzenie docisku slupa do podwaliny

Powierzchnia docisku do podwaliny:

A_d = 150*150 = 22500 mm²

k_mod = 0,9

γ_M. = 1,3

f_c,90,d = f_c,90,k * k_mod / γ_M. = 5,7*0,9/1,3 = 3,95 MPa

σ_c,90,d = P / A_d = 34,38*10³ / 22500 = 1,528 MPa

σ_c,90,d ≤ f_c,90,d * k_c,90

k_c,90 - wspolczynnik , który uwzglednia mozliwosc zwiekszenia wytrzymalosci kiedy dlugosc obciazonego odcinka, wznikajaca z rozkladu sily,

k_c,90 = 1 + ( 150 - l ) 170

dla a ≥ 100mm, l₁= 150 mm, l = 100 mm

k_c,90 = 1 + ( 150 - l00 ) 170 = 1,29

σ_c,90,d = 1,528 MPa ≤ f_c,90,d * k_c,90 = 1,29*3,95 = 5,09 MPa

Warunek SGN zostal spelniony.

1.2.8. Wymiarowanie mieczy

Przyjęto miecze usytuowane ukosnie pod katem α = 45° między platwia a slupem, o przekroju 100×100 i dlugosci l = 1,13 m.

Miecz obliczylam jako sciskany sila osiowa S = 31,77 kN

Przekroj mieczy:

A_d = 100*100 = 10000 mm²,

I_y = I_z = a⁴ / 12 = 833*10⁴

i_y = i_z = pierw (I/A) = 28,9 mm,

l_z =l_y = 1130mm,

λ_z = l_y / i_y = 1130 / 28,9 = 39,1 - smuklosc względem osi y

σ_c,crit,y = π²*E_0,05 / λ²_y

σ_c,crit,y = π²*8000 / 39,1² =16,43 MPa,

λ_rel,y =pierwiastek( f _c,0,k / σ_c,crit,y ) = 1,18, f _c,0,k = 23,00

k_y = 0,5[1 + β_c (λ_rel,y - 0,5) +λ²_rel,y ]

β_c - wspol. dotyczacy prostoliniowosci elementow ( dla drewna litego β_c = 0,2 )

k_y = 0,5[1 + 0,2*(1,18 - 0,5) +1,18²] = 1,264

k_c,y = 1 / [k_y + pierw( k_y² - +λ²_rel,y )]

k_c,y = 1 / [ 1,264 + pierw( 1,264² - 1,18²) = 0,334

σ_c,0,d = S / A_d = 31,77*10³ / 10000 = 3,177 MPa

σ_c,0,d / k_c,y*f_c,0,d + σ_m.,y,d / f_m,y,d + k_m ( σ_m.,z,d / f_m,z,d ) ≤ 1,

3,177 / 0,334*15,92 + 0 + 0 = 0,597 < 1,

Warunek SGN zostal spelniony.

---