Przykład 1: Siła czynna P działa na punkt materialny pod kątem α względem toru, po którym może poruszać się punkt.
Px=Pcosα; Py=Psinα; Ry=Py;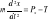
;Przykład 2: Punkt materialny porusza się pod wpływem siły ciężkości po równi pochyłej o kącie α.
Px=Gsinα; N=Gcosα; G=mg; T=μN=μmgcosα;Przykład 3: Znaleźć przyśpieszenie ciała o masie m, do którego przyłożono siłę P pod kątem α względem płaszczyzny ruchu.
N=G-Py; Ry=N; Px=Pcosα; Py=Psinα; max=Px-T;Małe drgania liniowe: Ruch punktu materialnego pod wpływem siły Px proporcjonalnej do wychylenia od stanu równowagi: Px=-cx; Równanie dynamiki ruchu:
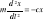
; Rozwiązanie ogólne: x=C1sinω0t+C2cosω0t; Pulsacja drgań własnych: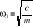
;Małe drgania liniowe z tłumieniem: Oprócz siły Px proporcjonalnej do wychylenia działa siła oporu ruchu Rx proporcjonalna do prędkości: Rx=-ανx; Równanie dynamiki ruchu:
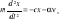
; Podstawiając: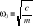
;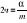
; otrzymujemy: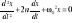
- równanie różniczkowe 2-go rzędu o stałych współczynnikach. Rozwiązanie: 1) Jeżeli n<ω0 (małe tłumienie) - drgania tłumione: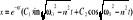
; 2) Jeżeli n>ω0 (duże tłumienie) - przebieg aperiodyczny: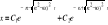
; 3) Jeżeli n=ω0 - przebieg aperiodyczny krytyczny: x=C1e-nt+C2te-nt;Ruch krzywoliniowy nieswobodnego punktu materialnego: Punkt nieswobodny może poruszać się tylko wzdłuż krzywoliniowego toru, niezależnie od kierunku działania wypadkowej siły czynnej P. W równaniu dynamiki oprócz siły czynnej P należy również uwzględnić siłę reakcji więzów R:
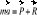
;Zasada d'Alemberta: Podczas ruchu punktu materialnego, w każdej chwili wszystkie siły rzeczywiste działające na punkt oraz siła bezwładności pozostają w równowadze. Siła bezwładności (siła d'Alemberta):
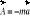
; Siła bezwładności jest zawsze skierowana przeciwnie do przyśpieszenia. Zasada d'Alemberta umożliwia stosowanie równań równowagi sił znanych ze statyki do analizy dynamiki ruchu punktu materialnego: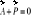
;Pęd punktu materialnego: Z drugiej zasady dynamiki Newtona wynika, że:
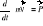
; gdzie wektor: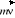
- to pęd punktu materialnego. Wektor pędu punktu materialnego ma kierunek i zwrot prędkości.Zasada zachowania pędu: Jeśli na punkt nie działa żadna siła lub działają siły równoważące się, to pęd tego punktu jest wielkością stałą.
Pęd układu punktów materialnych: Pęd układu n punktów materialnych:
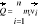
; Pochodna względem czasu pędu układu punktów materialnych jest równa sumie geometrycznej wszystkich sił zewnętrznych działających na punkty układu: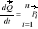
; Siły wewnętrzne nie mogą spowodować zmiany pędu układu punktów materialnych. Jeśli na układ nie działają żadne siły zewnętrzne lub działają siły, których suma geometryczna jest równa zeru, to całkowity pęd układu pozostaje stały. Pęd układu punktów materialnych jest równy iloczynowi masy całkowitej układu i prędkości jego środka masy: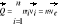
; gdzie: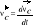
;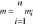
;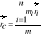
; - promień wodzący środka masy układu.Impuls siły: Jeżeli w przedziale czasu <t1,t2> na punkt materialny działa stała siła P, to impuls siły S jest dany wzorem:
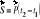
; W przypadku ogólnym (siła zmienna w czasie):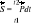
; Zmiana pędu punktu materialnego w skończonym przedziale czasu jest równa impulsowi siły działającej na ten punkt w tym samym czasie: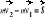
; W przypadku ogólnym, gdy na układ punktów materialnych działają dowolne siły zewnętrzne, przyrost pędu układu wyraża się wzorem: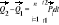
; Przyrost pędu układu punktów materialnych w skończonym przedziale czasu jest równy sumie geometrycznej impulsów sił zewnętrznych: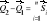
;Moment pędu (kręt) punktu materialnego: Moment pędu względem bieguna 0:
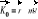
;
;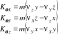
; Jeśli: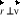
, to: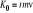
; Moment pędu względem danej osi jest równy składowej na tę oś momentu pędu względem bieguna 0.Pochodna momentu pędu:
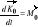
; Moment siły P względem bieguna 0: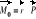
; Pochodna momentu pędu względem bieguna (lub osi) równa jest momentowi wypadkowej siły względem tego bieguna (osi).Zasada zachowania momentu pędu: Jeżeli moment wypadkowej siły zewnętrznej względem bieguna (lub osi) jest równy zeru, to moment pędu względem tego bieguna (osi) pozostaje stały.
Moment pędu bryły sztywnej:
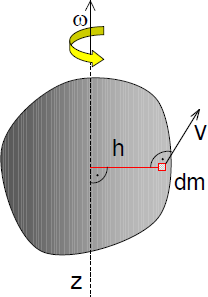
Prędkość liniowa elementu dm: ν=ωh; Moment pędu elementu dm względem osi z: dKz=h*dm*ν=ωh2dm; Całkowity moment pędu bryły względem osi z: ![]()
; Moment bezwładności bryły względem osi z: ![]()
;
Moment bezwładności bryły: Definicja: Momentem bezwładności bryły sztywnej względem danej osi nazywa się granicę, do której dąży suma iloczynów mas elementów, na które myślowo bryła została podzielona, przez kwadraty odległości tych elementów od osi:
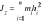
; Po przejściu do granicy: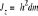
;Przykład 1: Obl. moment bezwładności jednorodnego pręta o masie m i długości l względem osi przechodzącej przez jego: a) środek:
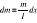
;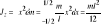
; b) koniec:
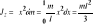
;Przykład 2: Obliczyć moment bezwładności jednorodnego walca o masie m i promieniu R względem jego osi symetrii:
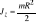
; (więcej na wykładach nie było).Równanie dynamiki ruchu obrotowego bryły sztywnej: Iloczyn momentu bezwładności bryły sztywnej względem osi obrotu i przyśpieszenia kątowego jest równy sumie momentów względem osi obrotu wszystkich sił zewnętrznych.
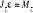
; Po uwzględnieniu definicji przyśpieszenia kątowego otrzymuje się równanie różniczkowe 2-go rzędu względem kąta obrotu: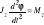
;Energia kinetyczna: Energia kinetyczna punktu materialnego: E=1/2mν2; Energia kinetyczna układu n punktów materialnych:
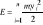
; Energia kinetyczna ciała sztywnego poruszającego się ruchem postępowym: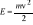
Wyszukiwarka
Podobne podstrony:
Ident obiekt h(t), Politechnika Lubelska, Studia, Semestr 6, Egzaminy, automatyka, AUTOMATYKA
Ochrona patentowa, Politechnika Lubelska, Studia, Semestr 6, Egzaminy
Ściąga zadania, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, sieci
Funkcja opisujaca pop1, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, automatyka, AUTOMATYKA
Ściąga zadania (2), Politechnika Lubelska, Studia, Semestr 6, Egzaminy, sieci
IGBT, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, Surtel, Elektronika i energoelektronika (S
Falowniki, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, Surtel, Ściągi, Falowniki
energoelektronika surtel pytania, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, Surtel, Ściągi
instalacje odpowiedzi, Politechnika Lubelska, Studia, Semestr 6, Egzaminy
Automatyka pytania egzamin, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, automatyka
UKŁADY KOMBINACYJNE, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, automatyka, AUTOMATYKA
TRIAK, Politechnika Lubelska, Studia, Semestr 6, Egzaminy, Surtel, Elektronika i energoelektronika (
Ident obiekt h(t), Politechnika Lubelska, Studia, Semestr 6, Egzaminy, automatyka, AUTOMATYKA
Teoria niezawodności, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, ŚĆIĄGAWKI, Teor
Urządzenia 100 - przekładniki prądowe (tylko dla ZAOCZNYCH), Politechnika Lubelska, Studia, semestr
Drgania Ćwiczenie nr 13, Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, Laborka, Lab
Urządzenia 101 - parametry łączników protokół (tylko dla ZAO, Politechnika Lubelska, Studia, semestr
więcej podobnych podstron