Wydział Fizyki i Techniki Jądrowej		Grzegorz Sawina , Sebastian Wroński			Zespół 1
Rok 2 , Grupa 3		Temat : Próżnia . Własności gazu .			Nr.ćwicz 22
Data wyk. 2.11.99	Data oddania	Zwrot do pop.	Data oddania	Ocena :	Podpis :

Cel ćwiczenia

Zapoznanie się z ukladem próżniowym i pomiarem ciśnienia w tym układzie , sprawdzenie prawa Boyle'a - Mariotte'a dla powietrza w temperaturze pokojowej wyznaczenie uniwersalnej stałej gazowej.

Wprowadzenie teoretyczne.

Gaz doskonały

Zgodnie z teorią kinetyczno - molekularną gazem doskonałym nazywamy następujący uproszczony, wyidealizowany model gazu rzeczywistego:

a. Gaz składa się z identycznych cząsteczek

b. Cząsteczki znajdują się w ciągłym ruchu i podlegają zasadom dynamiki Newtona

c. Całkowita liczba cząsteczek jest bardzo duża

d. Objętość i rozmiary liniowe cząsteczek są zaniedbywalnie małe

e. Cząsteczki nie oddziałują między sobą za wyjątkiem samych zderzeń

f. Zderzenia są doskonale sprężyste i zachodzą w zaniedbywalnie krótkim czasie.

Równanie stanu gazu doskonałego dane jest wzorem:

gdzie:

p - ciśnienie gazu;

V - objętość;

n - liczba moli gazu;

R - uniwersalna stała gazowa.

Prawo Boyle`a - Mariotta:

Opisuje przemianę izotermiczą gazu doskonałego. Przemiana izotermiczna to taka w której T=const . Z równania stanu gazu doskonałego otrzymujemy:

pV = const = nRT, czyli

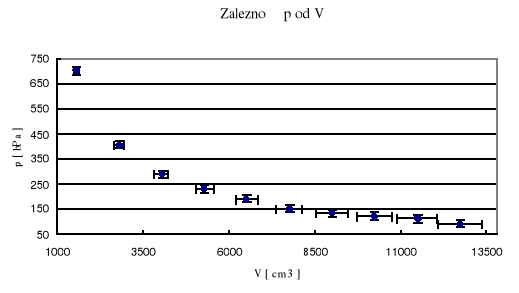
We współrzędnych p, V wykresem przemiany izotermicznej jest hiperbola.

Ciśnienie gazu wiąże się z oddziaływaniem cząsteczek z ściankami naczynia. Zderzając się z nimi oddają swoją energię i wywierają nacisk. Jednostką ciśnienia w układzie SI jest paskal [Pa]. Jest to ciśnienie wywierające nacisk jednego niutona na jeden metr kwadratowy. Jednostkami pochodnymi są : atmosfera techniczna , bar, atmosfera fizyczna, milimetr słupa rtęci ( tor ), etc.

Próżnią nazywamy stan, jaki panuje w obszarze wypełnionym gazami lub parami, gdy ciśnienie jest niższe od ciśnienia atmosferycznego.

Próżnię wytwarza się poprzez mechaniczne usunięcie cząsteczek powietrza poza obszar naczynia ( pompy przepływowe: rotacyjna i dyfuzyjna ) lub poprzez absorpcję ( pompy sorpcyjne ).

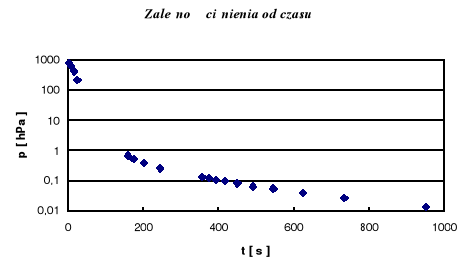
Pompę próżniową charakteryzują dwie wartości: ciśnienie końcowe i szybkość pompowania. Ciśnienie końcowe jest miarą próżni ustalonej po bardzo długim czasie pompowania, zależne jest w dużym stopniu od prądu wstecznego w pompie ( ilości gazu „cofającego się” ). C. k. dla pompy rotacyjnej równe jest w przybliżeniu 10^-1 - 10^-2 Pa , a dla pompy dyfuzyjnej 10^-6 - 10^-7 Pa. Szybkość pompowania S oznacza objętość gazu usuniętego w jednostce czasu. Definiowana jest funkcja zależności ciśnienia wewnątrz opróżnianego pojemnika od czasu ( S = const ) oznaczane p(t). Korzystając z definicji szybkości pompowania i różniczkując prawo Boyle`a - Mariotta otrzymujemy dla pojemnika o pojemności V:

Całkując stronami:

Technika próżniowa znajduje szerokie zastosowanie: w procesach produkcji związków o wysokiej czystości chemicznej i przyrządów półprzewodnikowych, w lampach kineskopowych, termosach i naczyniach do przechowywania skroplonych gazów. Największą jakość próżni uzyskuje się w komorach akceleratorowych - rzędu 10^-9 Pa

Rodzaje pomp :

pompa rotacyjna pompa dyfuzyjna

1. Olej 1. Chłodzenie cieczą

2. Obudowa 2. Olej

3. Sprężyna wypychająca tłoki 3. Grzejnik

4. Wlot 4. Wlot

5. Wylot 5. Wylot

Pompa rotacyjna jest pompą niskopróżniową. Za jej pomocą można uzyskać ciśnienie co najwyżej rzędu 10 ^-1 - 10 ^-7 [Pa]. Wewnątrz cylindrycznego naczynia (statora) obraca się, umocowany mimośrodowo, wirnik cylindryczny. Na jego średnicy znajdują się dwa suwaki dociskane sprężynami tak, żeby podczas obrotu ślizgały się po wewnętrznej powierzchni statora. Gdy powietrze z odpompowywanego zbiornika dostaje się do przestrzeni pomiędzy statorem a wirnikiem jej objętość powiększa się w trakcie ruchu aż do chwili, gdy drugi suwak minie ujście przewodu wylotowego odcinając ją od zbiornika. Przy dalszym ruchu obrotowym wirnika odcięte powietrze jest wypychane przez wylot.

Pompa dyfuzyjna wydala powietrze do próżni wstępnej. Może ona pracować jedynie w kaskadzie z pompami rotacyjnymi. W zbiorniku czynnika pompującego, zawierającego olej (rtęć), podgrzewanym grzejnikiem wytwarza się para, która dopływa prowadnicą do dyszy o parasolowatym kształcie. Cząsteczki pompowanego gazu dyfundują do wnętrza strumienia par i są unoszone. Na schłodzonych ściankach pompy strumień par ulega kondensacji i krople oleju (rtęci) spływają do zbiornika a gazy uchodzą do próżni wstępnej.

Próżniomierze mają za zadanie podać miarę próżni. Rozróżniamy próżniomierze: mechaniczne, hydrostatyczne, kompensacyjne, cieplnoprzewodnościowe, jonizacyjne i inne.

Manometr mechaniczny dokonuje pomiaru różnicy ciśnień pomiędzy ciśnieniem zewnętrznym a ciśnieniem wewnątrz pojemnika wykorzystując odkształcenie elementu mechanicznego, które przenoszone jest na wskazówkę.

Próżniomierz termoprzewodnościowy wykorzystuje zależność zmiany przewodnictwa cieplnego rozrzedzanego gazu od ciśnienia . Ciśnienie określa się przez pomiar jakiejś wielkości fizycznej, która zmienia się, gdy energia cieplna ulega zmianie. Istotną częścią próżniomierza stanowi element czujnikowy nagrzewany do temperatury T wyższej niż temperatura otoczenia T₀, co uzyskuje się przez doprowadzenie do czujnika mocy elektrycznej P. Przy danym układzie geometrycznym "czujnik-otoczenie" ciśnienie danego gazu może być wyrażone funkcją mocy i temperatury

p = f(P(U, I), T)

Dokładność próżniomierza cieplno-przewodniościowego wynosi 10 ^-1 - 10 ⁵ [Pa].

Wyniki pomiarów :

Warunki zewnętrzne

po= 996 ±1 hPa

T= 295 ±1 K

Vz= 1240 ±5% cm ³ - objętość zbiornika

Vp= 320 ±5% cm ³ - objętość przewodów łączących

Ciśnienie zostało przeliczone na hPa przy pomocy następujących przeliczników :

1 Tr = 1,33 hPa

1 kG/cm2 = 980,7 hPa

czas [ s ]	p [kG/cm2]	p [ hPa ]
4	0,2	799,86
8	0,4	603,72
16	0,6	407,58
26	0,8	211,44

czas [ s ]	p [ Tor ]	p [ hPa ]
160	0,5	0,665
176	0,4	0,532
203	0,3	0,399
246	0,2	0,266
357	0,1	0,133
375	0,09	0,1197
395	0,08	0,1064
418	0,07	0,0931
450	0,06	0,0798
494	0,05	0,0665
547	0,04	0,0532
626	0,03	0,0399
735	0,02	0,0266
951	0,01	0,0133

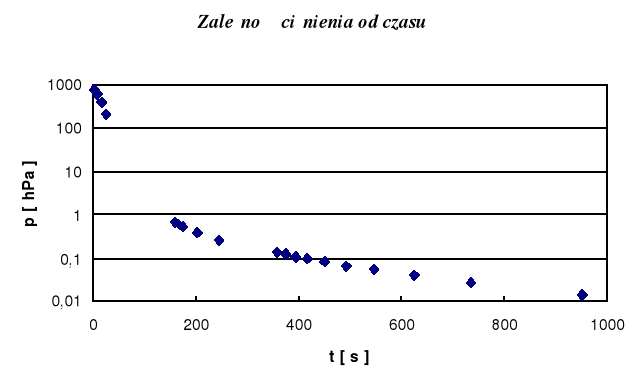
Wyniki pomiarów

Zbiornik	V [ cm3 ]	p [ kG/cm]	p [ hPa ]	1/v
0	1560	0,3	701,79	0,000641
1	2800	0,6	407,58	0,000357
2	4040	0,72	289,896	0,000248
3	5280	0,78	231,054	0,000189
4	6520	0,82	191,826	0,000153
5	7760	0,86	152,598	0,000129
6	9000	0,88	132,984	0,000111
7	10240	0,89	123,177	9,77E-05
8	11480	0,9	113,37	8,71E-05
9	12720	0,92	93,756	7,86E-05

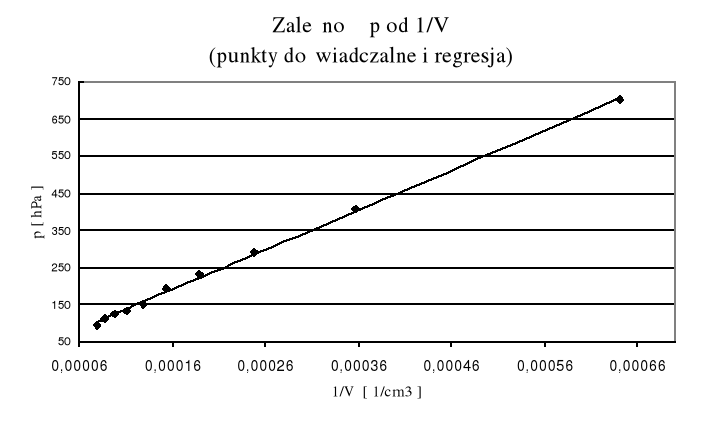
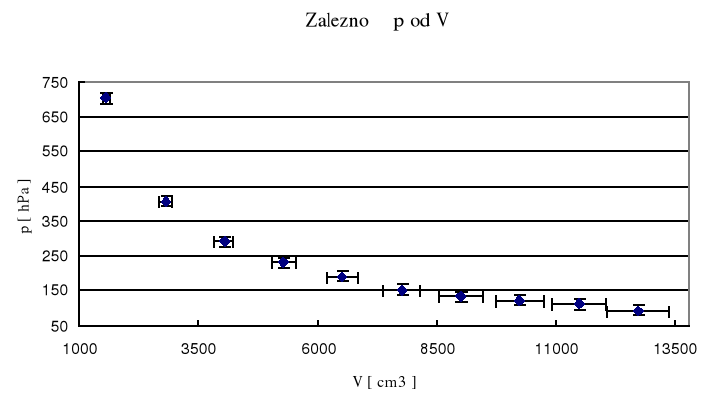
Aby dopasować prostą do zbioru punktów doświadczalnych stosujemy metodę najmniejszych kwadratów . Metoda ta polega na takim dobraniu parametrów prostej aby suma różnic wartości eksperymentalnych y_i i obliczonych ax_i+b była jak najmniejsza :

Kryterium to zapewnia najlepsze oszacowanie parametrów jeśli punktu pomiarowe obarczone są jednakowym błędem przypadkowym o rozkładzie Gaussa . Oby obliczy parametry prostej obliczamy najpierw średnie arytmetyczne dla zmiennych x oraz y :

określające położenie „ środka ciężkości ”
,
punktów eksperymentalnych , oraz wielkość D

będącą sumą kwadratów odchyłek wartości
od średniej
. Parametry prostej oblicza się wg wzorów :

,

Następnie obliczamy Dy która jest oszacowaniem odchylenia standardowego punktów do dopasowanej prostej .

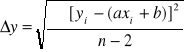
Wartość tą wykorzystujemy do obliczenia błędów standardowych parametrów prostej , które wyrażają się wzorami :

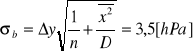
Analiza błędu :

Do pomiaru ciśnienia użyto manometru mechanicznego o klasie 1,5 oraz manometru termo-przewodnościowego który jednak posiadał skale nieliniową tak wiec nie jesteśmy w stanie określić błędu z jakim dokonywano pomiaru . Możemy natomiast określić błąd pomiaru manometrem mechanicznym który obliczamy:

Ciśnienie atmosferyczne odczytywane było z baromertu o dokładności 1 hPa a temperatura z termometru o dokładności 1 K . Natomiast dokładność objętości przyjeliśmy 5% .

Wnioski :

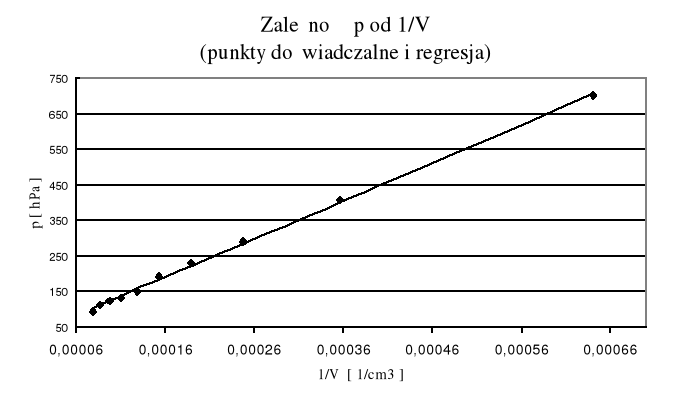
Nie udało się nam potwierdzić prawa Boyle'a-Mariotta ponieważ b nie jest statystycznie zaniedbywalne, czyli zależność między ciśnieniem, a objętością nie jest ściśle hiperboliczna.

Wpływ na takie wyniki mogła mieć zbyt mała efektywność pompy i otrzymana próżnia nie była wystarczająco niska co miało później wpływ na otrzymane wyniki. Wyszło nam, że przy nieskończonej objętości będziemy mieli skończone ciśnienie, a teoria przewiduje, że jego wartość będzie wynosiła zero. Teoria oczywiście traktuje o gazach idealnych, ale w powietrze w naszym doświadczeniu spełnia dość dobrze role gazu doskonałego. Można jeszcze zwrócić uwagę , że otrzymane przez nas a=nRT gdzie n- liczba moli, R- stała gazowa, a T to temperatura w kelwinach.

Można więc policzyć liczbę moli znając a. Stosując wzór p_oV_o=nRT, gdzie p_o jest ciśnieniem atmosferycznym, a V_o objętością butli, którą dekompresujemy można obliczyć liczbę n moli powietrza.

	wartość	błąd
Vo[m^3]	1,24E-03	6,20E-05
Po[Pa]	99600	100
R[j/mol*K]	8,3144
T[K]	295	1
a[j]	107	1,32
n=a/RT	0,043625	0,0006
n=pV/RT	0,050353	0,003

Widać, że wyniki różnią się, a różnica ta nie mieści się w granicy błędu, choć wyniki są do siebie zbliżone. Jest to to najprawdopodobniej spowodowane przez znaczące b.

Wyjaśnienie dlaczego b nie jest statystycznie zaniedbywalne jest trudne. Opierając się na wykresie można zaobserwować, że punkt przy najmniejszym ciśnieniu jest najbardziej rozbieżny z krzywą regresji stąd nasuwa się na myśl, że jeżeli mielibyśmy więcej pojemników, a co za tym idzie więcej pomiarów dla małych wartości 1/V, wówczas te punkty też byłyby znacznie odchylone od prostej regresji przez nas wyznaczonej, a co za tym idzie mogłyby mieć większą wagę w wyznaczeniu nowej regresji. Bo regresja jest dopasowane najlepiej ale tylko do naszych punktów pomiarowych.

---